En el mundo prevalecen los sistemas de interacción entre múltiples agentes, desde los sistemas puramente físicos hasta los complicados sistemas dinámicos sociales. Las interacciones entre entidades/componentes pueden dar lugar a patrones de comportamiento muy complejos tanto a nivel de individuos como del sistema multiagente en su conjunto. Dado que normalmente sólo se observan las trayectorias de las entidades individuales sin ningún conocimiento de los patrones de interacción subyacentes, y que normalmente hay múltiples modalidades posibles para cada agente con incertidumbre, es un reto modelar sus dinámicas y prever sus comportamientos futuros.
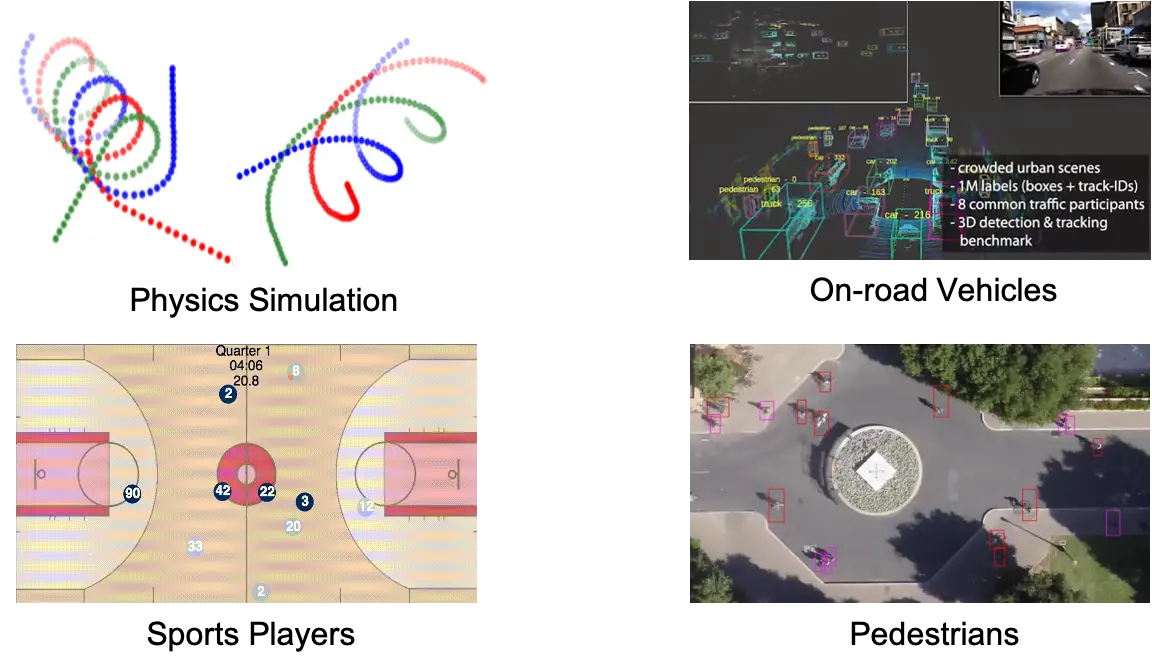
Figura 1. Típicos sistemas interactivos multiagente.
En muchas aplicaciones del mundo real (por ejemplo, los vehículos autónomos, los robots móviles), la comprensión efectiva de la situación y la predicción precisa de la trayectoria de los agentes interactivos desempeñan un papel importante en las tareas posteriores, como la toma de decisiones y la planificación. Presentamos un marco genérico de predicción de trayectorias (denominado EvolveGraph) con reconocimiento explícito de la estructura relacional y predicción mediante gráficos de interacción latente entre múltiples agentes interactivos heterogéneos. Teniendo en cuenta la incertidumbre de los comportamientos futuros, el modelo está diseñado para proporcionar hipótesis de predicción multimodal. Dado que las interacciones subyacentes pueden evolucionar incluso con cambios abruptos a lo largo del tiempo, y que las diferentes modalidades de evolución pueden conducir a resultados diferentes, abordamos la necesidad de un razonamiento relacional dinámico y de la evolución adaptativa de los gráficos de interacción.
Desafíos de la predicción del comportamiento de múltiples agentes
Figura 2. Una ilustración de un escenario típico de intersección urbana.
Utilizamos un escenario de intersección urbana con múltiples participantes del tráfico que interactúan como un ejemplo ilustrativo para elaborar los principales desafíos de la tarea de predicción del comportamiento de múltiples agentes.
-
En primer lugar, puede haber agentes heterogéneos que tengan patrones de comportamiento distintos, por lo que utilizar un modelo homogéneo de dinámica/comportamiento puede no ser suficiente. Por ejemplo, hay diferentes restricciones y normas de tráfico para los vehículos y los peatones. Más concretamente, las trayectorias de los vehículos están estrictamente limitadas por la geometría de la carretera y sus propios modelos cinemáticos; mientras que los comportamientos de los peatones son mucho más flexibles.
-
En segundo lugar, puede haber varios tipos de patrones de interacción en un sistema multiagente. Por ejemplo, la interacción entre vehículos, entre peatones y entre vehículos y peatones en el mismo escenario presentan pautas muy diferentes.
-
En tercer lugar, las pautas de interacción pueden evolucionar con el tiempo a medida que la situación cambia. Por ejemplo, cuando un vehículo va en línea recta, sólo necesita considerar el comportamiento del vehículo que va delante; sin embargo, cuando el vehículo planea cambiar de carril, también es necesario tener en cuenta los vehículos del carril de destino, lo que lleva a un cambio en los patrones de interacción.
-
Por último, pero no menos importante, puede haber incertidumbres y multimodalidades en los comportamientos futuros de cada agente, lo que lleva a varios resultados. Por ejemplo, en una intersección, el vehículo puede ir recto o tomar una curva.
En este trabajo, dimos un paso adelante para manejar estos desafíos y proporcionamos un marco genérico para la predicción de la trayectoria con un razonamiento relacional dinámico para los sistemas multiagente. Más específicamente, abordamos el problema de
- extrayendo los patrones de interacción subyacentes con una estructura gráfica latente, que es capaz de manejar diferentes tipos de agentes de forma unificada,
- capturando la dinámica de la evolución del gráfico de interacción para el razonamiento relacional dinámico,
- la predicción de trayectorias futuras (secuencias de estado) basadas en las observaciones históricas y el gráfico de interacción latente, y
- capturando la incertidumbre y la multimodalidad de los futuros comportamientos del sistema.
Razonamiento relacional con representación gráfica
Gráfico de Observación y Gráfico de Interacción
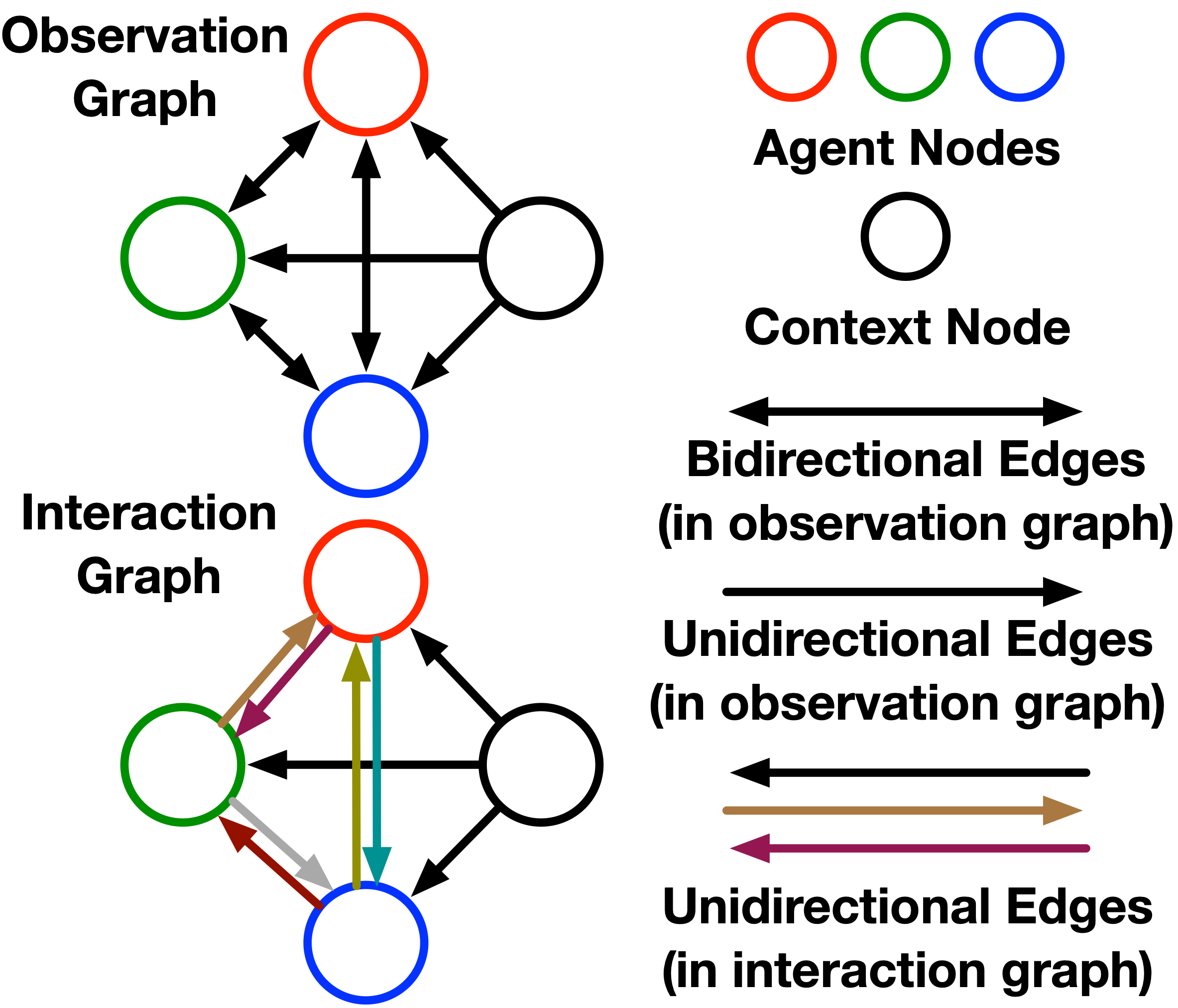
Figura 3. Una ilustración del gráfico de observación y del gráfico de interacción.
El sistema de interacción entre múltiples agentes se representa naturalmente en un gráfico, en el que los agentes se consideran como nodos y sus relaciones se consideran como bordes. Tenemos dos tipos de gráficos para diferentes propósitos, que se presentan a continuación:
- Gráfico de observación: El gráfico de observación tiene por objeto extraer incrustaciones de características de las observaciones en bruto, que consiste en nodos de agentes N y un nodo de contexto. Los nodos agentes están conectados bidireccionalmente entre sí, y el nodo de contexto sólo tiene bordes salientes a cada nodo agente. Cada nodo agente tiene dos tipos de atributos: autoatributo y atributo social. El primero sólo contiene la información de estado del propio nodo, mientras que el segundo sólo contiene la información de estado de los demás nodos.
- Gráfico de interacción: Usamos diferentes tipos de bordes para representar distintos patrones de interacción. Si no hay borde entre un par de nodos significa que los dos nodos no tienen relación. El gráfico de interacción representa patrones de interacción con una distribución de tipos de borde para cada borde, que se construye sobre el gráfico de observación.
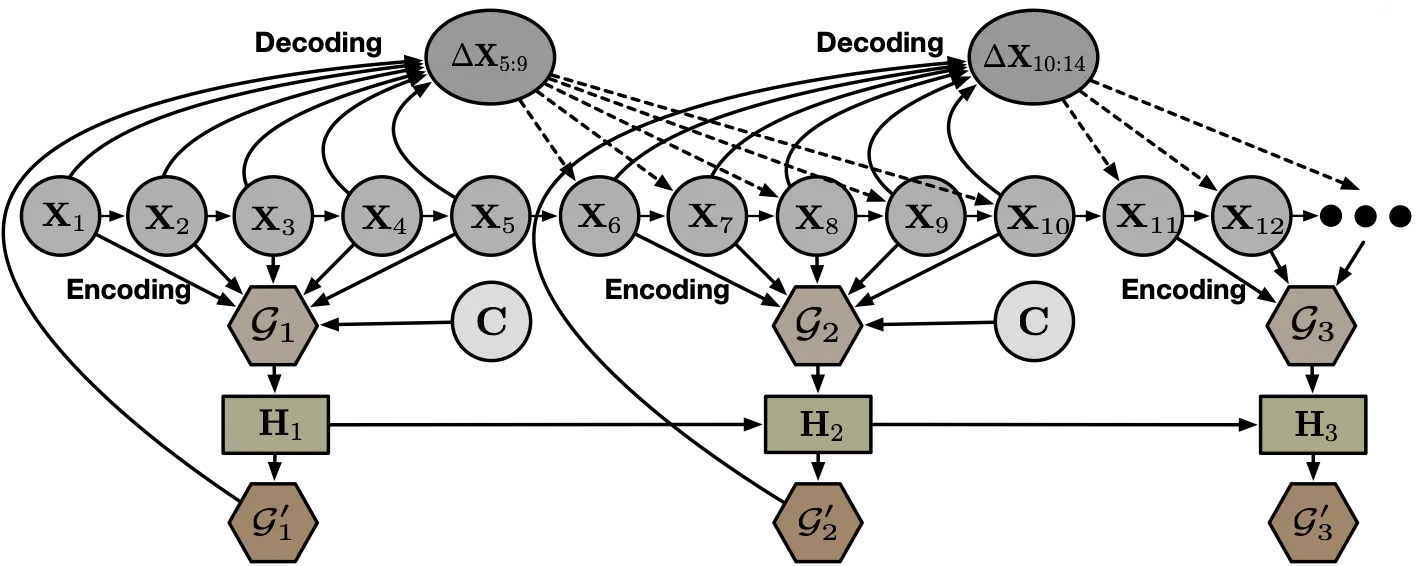
Figura 4. Una ilustración gráfica de alto nivel de EvolveGraph.
Aprendizaje de Gráficos de Interacción Dinámica
En muchas situaciones, es probable que las pautas de interacción reconocidas de los pasos de tiempo pasados no sean estáticas en el futuro. Además, muchos sistemas de interacción tienen propiedades multimodales en la naturaleza. Es probable que las diferentes modalidades que se apliquen después den lugar a diferentes pautas de interacción y resultados. Por lo tanto, hemos diseñado un proceso evolutivo dinámico de las pautas de interacción.
Como se ilustra en la figura 4, el proceso de codificación se repite cada paso de tiempo de τ (brecha de recodificación) para obtener el gráfico de interacción latente basado en el último gráfico de observación. Se utiliza una unidad recurrente (GRU) para mantener y propagar la información de la historia, así como para ajustar los gráficos de interacción anteriores. Se pueden encontrar más detalles en nuestro artículo.
Incertidumbre y multimodalidad
Aquí hacemos hincapié en los esfuerzos para fomentar la predicción y generación de trayectorias diversas y multimodales. En nuestro marco, la incertidumbre y la multimodalidad provienen principalmente de tres aspectos:
- En primer lugar, en el proceso de decodificación, obtenemos distribuciones de mezcla gaussiana que indican que hay varias modalidades posibles en el siguiente paso. Sólo tomamos muestras de un único componente gaussiano en cada paso, basadas en los pesos de los componentes que indican la probabilidad de cada modalidad.
- Segundo, diferentes trayectorias muestreadas llevarán a una evolución diferente de la gráfica de interacción. La evolución de los gráficos de interacción contribuye a la multimodalidad de los comportamientos futuros, ya que las diferentes estructuras relacionales subyacentes imponen diferentes regulaciones sobre el comportamiento del sistema y conducen a varios resultados.
- En tercer lugar, el entrenamiento directo de un modelo de este tipo, sin embargo, tiende a colapsar a un modo único. Por lo tanto, empleamos un mecanismo efectivo para mitigar el problema del colapso del modo y fomentar la multimodalidad. Durante el entrenamiento, llevamos a cabo el proceso de decodificación d veces, que genera trayectorias para cada agente bajo escenarios específicos. Sólo elegimos la hipótesis de predicción con la mínima pérdida para la retropropagación, que es la más probable que esté en el mismo modo que la verdad de la tierra. Las otras hipótesis de predicción pueden tener una pérdida mucho mayor, pero no implica necesariamente que sean inverosímiles. Pueden representar otras posibles modalidades razonables.
Experimentos
Destacamos los resultados de dos estudios de caso sobre un sistema de física sintética y un escenario de conducción urbana. Más detalles experimentales y casos de estudio sobre peatones y deportistas se pueden encontrar en nuestro artículo.
Estudio de caso 1: Sistema de Física de Partículas
Experimentamos con un sistema de partículas simulado con un cambio de relaciones. Múltiples partículas están inicialmente vinculadas y se mueven juntas. Los vínculos desaparecen siempre que se cumpla un determinado criterio sobre el estado de las partículas y, a partir de entonces, las partículas se mueven de forma independiente. Se espera que el modelo aprenda el criterio por sí mismo y realice tanto la predicción del tipo de borde como la predicción de la trayectoria. Dado que el sistema es de naturaleza determinista, no consideramos la multimodalidad en esta tarea.
Predijimos los estados de las partículas en los futuros 50 pasos de tiempo basados en las observaciones de 20 pasos de tiempo. Establecimos dos tipos de bordes en esta tarea, que corresponden a «con enlace» y «sin enlace». Los resultados de la predicción del tipo de borde se resumen en la Tabla 1, que se promedian en 3 ejecuciones independientes. «Sin cambio» significa que la estructura de interacción subyacente se mantiene igual en todo el horizonte, mientras que «Cambio» significa que el cambio de los patrones de interacción ocurre en algún momento. Muestra que la línea de base de aprendizaje supervisado, que entrena directamente las funciones de codificación con etiquetas de verdad de la tierra, funciona mejor en ambas configuraciones y sirve como «patrón oro». En la configuración «Sin cambios», NRI (dinámico) es comparable a EvolveGraph (recodificación RNN), mientras que EvolveGraph (estático) logra el mejor rendimiento. La razón es que la evolución dinámica del gráfico de interacción conduce a una mayor flexibilidad pero puede dar lugar a una mayor incertidumbre, lo que afecta a la predicción de los bordes en los sistemas con estructuras relacionales estáticas. En la configuración «Cambio», NRI (dinámico) reevalúa el gráfico latente en cada paso temporal durante la fase de prueba, pero es difícil captar la dependencia entre los gráficos consecutivos, y las funciones de codificación pueden no ser lo suficientemente flexibles para captar la evolución. EvolveGraph (recodificación RNN) funciona mejor porque considera la dependencia de pasos consecutivos durante la fase de capacitación, pero aún así captura la evolución sólo a nivel de característica en lugar de a nivel de gráfico. EvolveGraph (dinámico) logra una precisión significativamente mayor que las otras líneas de base (excepto la supervisada), debido a la evolución explícita de los gráficos de interacción.

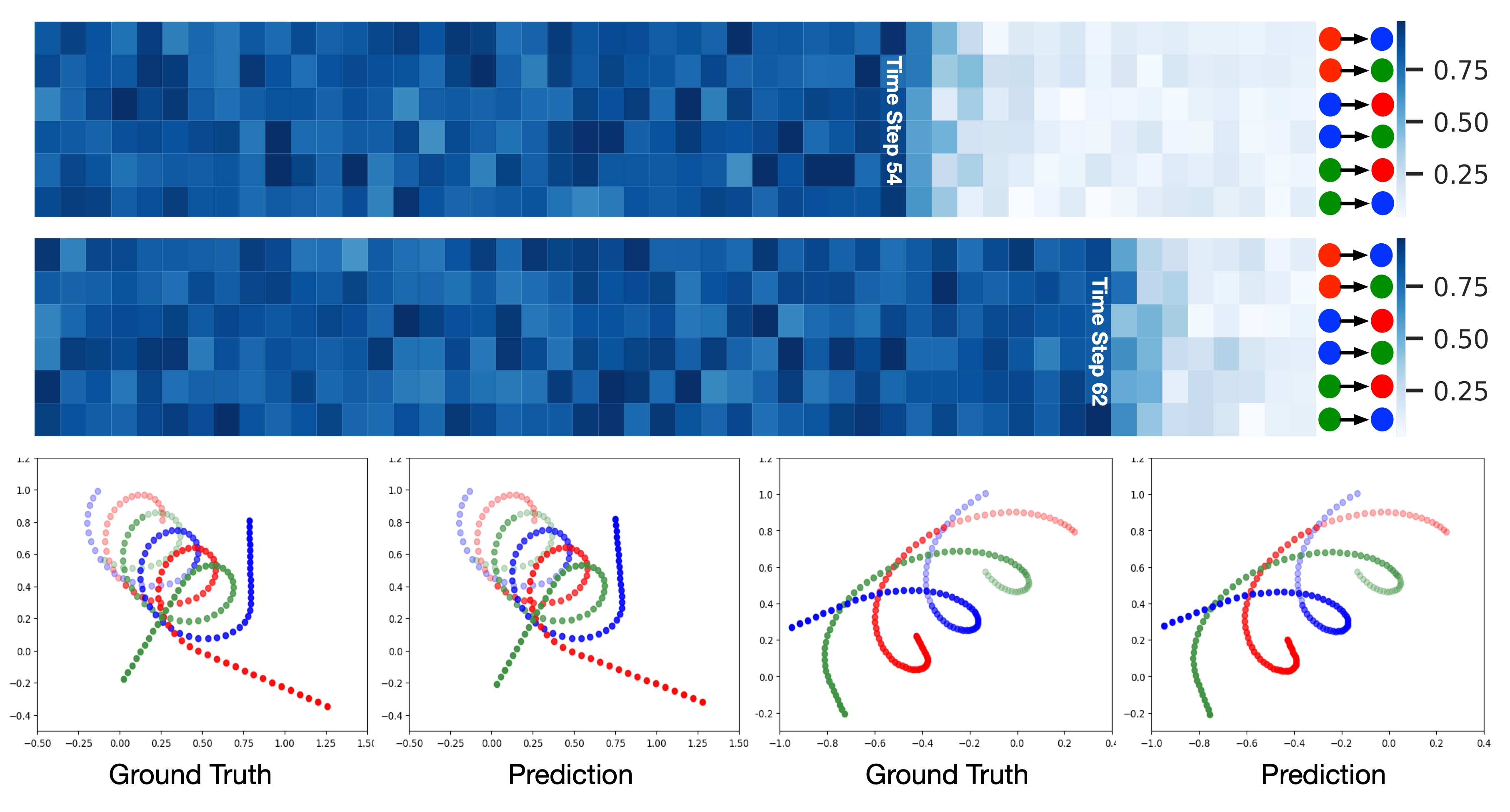
Figura 5. Visualización de la evolución del gráfico de interacción latente y de las trayectorias de las partículas. a) Las dos figuras superiores muestran la probabilidad del primer tipo de borde («con enlace») en cada paso de tiempo. Cada fila corresponde a un determinado borde (que se muestra a la derecha). Los tiempos reales de la evolución del gráfico son 54 y 62, respectivamente. El modelo es capaz de captar el criterio subyacente de cambio de relación y predecir además el cambio de los tipos de borde con casi ningún retraso. b) Las figuras de la última fila muestran los resultados de la predicción de la trayectoria, donde los puntos semitransparentes son observaciones históricas.
Estudio de caso 2: Escenarios de tráfico

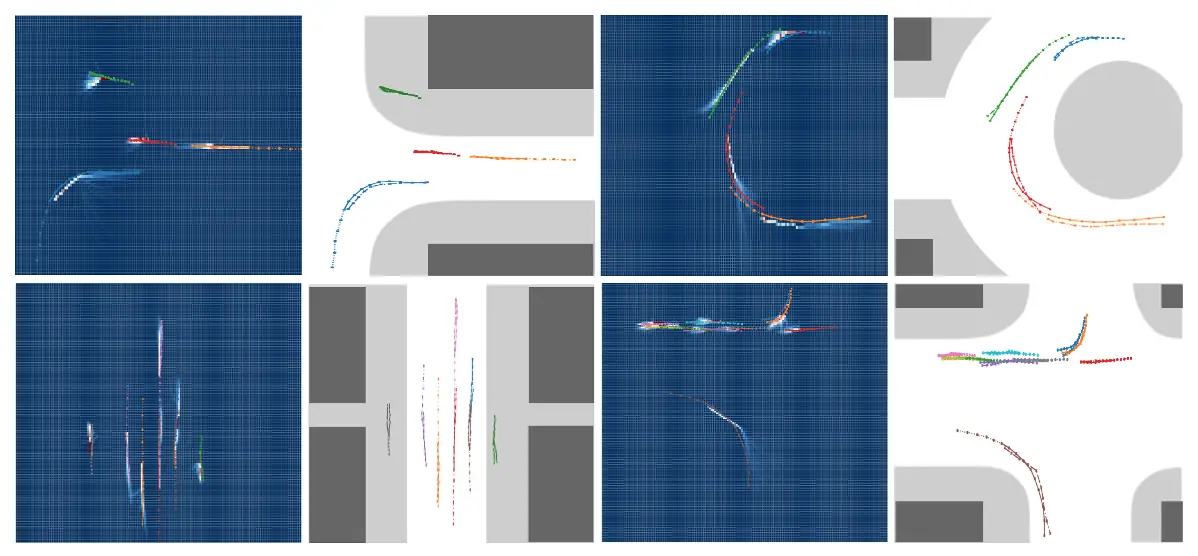
Figura 6. Visualización de casos de prueba en escenarios de tráfico. Las líneas discontinuas son trayectorias históricas, las líneas sólidas son verdades del terreno y las líneas discontinuas son hipótesis de predicción. Las áreas blancas representan las áreas de conducción y las áreas grises representan las aceras. Trazamos la hipótesis de predicción con el error de predicción promedio mínimo, y la carta térmica para representar las distribuciones.
Predijimos los futuros 10 pasos de tiempo (4.0s) basados en los 5 pasos de tiempo históricos (2.0s). La comparación de los resultados cuantitativos se muestra en la Tabla 2, donde la unidad de reporte y es metros en las coordenadas mundiales. Todos los métodos de línea de base consideran las relaciones e interacciones entre los agentes. El Social-Attention emplea mecanismos de atención espacial, mientras que el Social-GAN demuestra un profundo modelo generativo que aprende la distribución de los datos para generar trayectorias similares a las humanas. Tanto el Gated-RN como el Trajectron++ aprovechan la información espacio-temporal para implicar el razonamiento relacional, lo que conduce a un menor error de predicción. La NRI infiere un gráfico de interacción latente y aprende la dinámica de los agentes, lo que logra un rendimiento similar al de Trajectron++. El STGAT y la Social-STGCNN aprovechan además la red neuronal del gráfico para extraer características relacionales en el entorno multiagente. El método que proponemos logra el mejor rendimiento, lo que implica las ventajas de un modelo de interacción explícito a través de gráficos de interacción evolutivos. Los 4,0s / se reducen significativamente en un 20,0% / 27,1% en comparación con el mejor enfoque de línea de base (STGAT).
En la figura 6 se muestra la visualización de algunos casos de pruebas. Nuestro marco puede generar trayectorias precisas y plausibles. Más específicamente, en el caso superior izquierdo, para la hipótesis de la predicción azul en la parte inferior izquierda, hay un cambio abrupto en el quinto paso de la predicción. Esto se debe a que el gráfico de interacción evolucionó en este paso. Además, en la carta térmica, hay múltiples trayectorias posibles a partir de este punto, que representan múltiples modalidades potenciales. Estos resultados muestran que el gráfico de interacción evolutivo puede reforzar la propiedad multimodal de nuestro modelo, ya que diferentes muestras de trayectorias en los pasos anteriores conducen a diferentes direcciones de evolución del gráfico, lo que influye significativamente en la predicción posterior. En el caso de la parte superior derecha, cada coche puede salir de la rotonda en cualquier salida. Nuestro modelo puede mostrar con éxito las modalidades de salida de la rotonda y de permanencia en ella. Además, al salir de la rotonda, se predice que los coches saldrán por su derecha, lo que implica que las modalidades predichas por nuestro modelo son plausibles y razonables.
Resumen y aplicaciones más amplias
Presentamos EvolveGraph, un marco genérico de predicción de trayectorias con un razonamiento relacional dinámico, que puede manejar sistemas interactivos en evolución que implican múltiples agentes interactivos heterogéneos. El marco propuesto podría aplicarse a una amplia gama de aplicaciones, desde sistemas puramente físicos hasta sistemas complejos de dinámica social. En este blog se muestran algunas aplicaciones ilustrativas a los objetos físicos y a los participantes en el tráfico. El marco también podría aplicarse para analizar y predecir la evolución de sistemas interactivos más grandes, como sistemas físicos complejos con un gran número de componentes interactivos, redes sociales y flujos de tráfico macroscópicos. Aunque ya existen trabajos que utilizan redes neuronales gráficas para manejar tareas de predicción de trayectorias, aquí enfatizamos el impacto de utilizar nuestro marco para reconocer y predecir la evolución de las relaciones subyacentes. Con estructuras relacionales precisas y razonables, podemos predecir o generar comportamientos plausibles del sistema, que ayudan mucho a la toma de decisiones óptimas u otras tareas posteriores.
Agradecimientos: Agradecemos a todos los coautores del artículo «EvolveGraph»: Multi-Agente de predicción de trayectoria con Razonamiento Relacional Dinámico» por sus contribuciones y discusiones en la preparación de este blog. Los puntos de vista y opiniones expresados en este blog son únicamente de los autores.
Esta entrada en el blog se basa principalmente en el siguiente documento:
EvolveGraph: Predicción de la trayectoria de múltiples agentes con razonamiento relacional dinámico
Jiachen Li*, Fan Yang*, Masayoshi Tomizuka, y Chiho Choi
Avances en los Sistemas de Procesamiento de Información Neural (NeurIPS), 2020
Actas, Preprint, Sitio web del proyecto, Recursos
A continuación se enumeran algunas otras obras conexas:
Sistema Neural Generativo Condicional para la Predicción de la Trayectoria Probabilística
Jiachen Li, Hengbo Ma, y Masayoshi Tomizuka
Conferencia Internacional de Robótica y Sistemas (IROS) del IEEE/RSJ, 2019
Procedimientos,
Preprint
El seguimiento multiagente consciente de la interacción y la predicción de la conducta probable a través del aprendizaje adverso
Jiachen Li*, Hengbo Ma*, y Masayoshi Tomizuka
IEEE Conferencia Internacional sobre Robótica y Automatización (ICRA), 2019
Procedimientos,
Preprint
Rastreo genérico y marco de predicción probabilístico y su aplicación en la conducción autónoma
Jiachen Li, Wei Zhan, Yeping Hu, y Masayoshi Tomizuka
Transacciones del IEEE sobre Sistemas de Transporte Inteligente, 2020
Artículo,
Preprint
