
Evolución diferencial es un algoritmo de optimización global.
Es un tipo de algoritmo evolutivo y está relacionado con otros algoritmos evolutivos como el algoritmo genético.
A diferencia del algoritmo genético, fue diseñado específicamente para operar sobre vectores de números con valores reales en lugar de cadenas de bits. Además, a diferencia del algoritmo genético, utiliza operaciones vectoriales como la resta y la suma de vectores para navegar por el espacio de búsqueda en lugar de transformaciones inspiradas en la genética.
En este tutorial, descubrirá el algoritmo de optimización global de Evolución Diferencial.
Después de completar este tutorial, sabrá:
- La optimización de la evolución diferencial es un tipo de algoritmo evolutivo que está diseñado para trabajar con soluciones candidatas de valor real.
- Cómo utilizar la API del algoritmo de optimización de Evolución Diferencial en Python.
- Ejemplos de uso de la evolución diferencial para resolver problemas de optimización global con múltiples óptimos.
Empecemos.

Optimización global de evolución diferencial con Python
Foto de Gergely Csatari, algunos derechos reservados.
Descripción general del tutorial
Este tutorial se divide en tres partes; son:
- Evolución diferencial
- API de evolución diferencial
- Ejemplo resuelto de evolución diferencial
Evolución diferencial
La Evolución Diferencial, o DE para abreviar, es un algoritmo estocástico de optimización de búsqueda global.
Es un tipo de algoritmo evolutivo y está relacionado con otros algoritmos evolutivos como el algoritmo genético. A diferencia del algoritmo genético que representa soluciones candidatas utilizando secuencias de bits, la evolución diferencial está diseñada para trabajar con soluciones candidatas multidimensionales de valor real para funciones objetivas continuas.
La evolución diferencial (DE) es posiblemente uno de los algoritmos estocásticos de optimización de parámetros reales más poderosos en uso actual.
– Evolución diferencial: una revisión del estado del arte, 2011.
El algoritmo no utiliza información de gradiente en la búsqueda y, como tal, se adapta bien a funciones objetivas no lineales no diferenciales.
El algoritmo funciona manteniendo una población de soluciones candidatas representadas como vectores de valor real. Las nuevas soluciones candidatas se crean mediante la creación de versiones modificadas de las soluciones existentes que luego reemplazan a una gran parte de la población en cada iteración del algoritmo.
Las nuevas soluciones candidatas se crean utilizando un «estrategia”Que implica seleccionar una solución base a la que se agrega una mutación y otras soluciones candidatas de la población a partir de la cual se calcula la cantidad y el tipo de mutación, llamado vector de diferencia. Por ejemplo, una estrategia puede seleccionar la mejor solución candidata como base y soluciones aleatorias para el vector de diferencia en la mutación.
DE genera nuevos vectores de parámetros sumando la diferencia ponderada entre dos vectores de población a un tercer vector.
– Evolución diferencial: una heurística simple y eficiente para la optimización global en espacios continuos, 1997.
Las soluciones base son reemplazadas por sus hijos si los hijos tienen una mejor evaluación de la función objetiva.
Finalmente, después de haber creado un nuevo grupo de niños, comparamos a cada niño con el padre que lo creó (cada padre creó un solo hijo). Si el hijo es mejor que el padre, reemplaza al padre en la población original.
– Página 51, Fundamentos de metaheurística, 2011.
La mutación se calcula como la diferencia entre pares de soluciones candidatas que da como resultado un vector de diferencia que luego se agrega a la solución base, ponderado por un hiperparámetro de factor de mutación establecido en el rango [0,2].
No todos los elementos de una solución base están mutados. Esto se controla mediante un hiperparámetro de recombinación y, a menudo, se establece en un valor grande, como el 80 por ciento, lo que significa que la mayoría, pero no todas, las variables en una solución base se reemplazan. La decisión de mantener o reemplazar un valor en una solución base se determina para cada posición por separado muestreando una distribución de probabilidad como un binomio o exponencial.
Se utiliza una terminología estándar para describir estrategias diferenciales con la forma:
Donde DE significa «evolución diferencial, » X define la solución base que se va a mutar, como «rand«Para aleatorio o»mejor”Para la mejor solución en la población. los y representa el número de vectores de diferencia añadidos a la solución base, como 1, y z define la distribución de probabilidad para determinar si cada solución se mantiene o se reemplaza en la población, como «compartimiento«Para binomio o»Exp”Para exponencial.
La convención general utilizada anteriormente es DE / x / y / z, donde DE significa «evolución diferencial», x representa una cadena que denota el vector base que se va a perturbar, y es el número de vectores de diferencia considerados para la perturbación de x, y z representa el tipo de cruce que se está utilizando (exp: exponencial; bin: binomial).
– Evolución diferencial: una revisión del estado del arte, 2011.
La configuración DE / best / 1 / bin y DE / best / 2 / bin son configuraciones populares ya que funcionan bien para muchas funciones objetivas.
Los experimentos realizados por Mezura-Montes et al. indican que DE / best / 1 / bin (utilizando siempre la mejor solución para encontrar direcciones de búsqueda y también binomial crossover) siguió siendo el esquema más competitivo, independientemente de las características del problema a resolver, basado en la precisión final y robustez de los resultados.
– Evolución diferencial: una revisión del estado del arte, 2011.
Ahora que estamos familiarizados con el algoritmo de evolución diferencial, veamos cómo podríamos usar la implementación de la API de SciPy.
API de evolución diferencial
El algoritmo de optimización global de Evolución Diferencial está disponible en Python a través de la función SciPy diferencial_evolution ().
La función toma el nombre de la función objetivo y los límites de cada variable de entrada como argumentos mínimos para la búsqueda.
|
... # realizar la búsqueda de evolución diferencial resultado = evolución_diferencial(objetivo, límites) |
Hay una serie de hiperparámetros adicionales para la búsqueda que tienen valores predeterminados, aunque puede configurarlos para personalizar la búsqueda.
Un hiperparámetro clave es el «estrategia”Argumento que controla el tipo de búsqueda de evolución diferencial que se realiza. De forma predeterminada, se establece en «best1bin”(DE / best / 1 / bin), que es una buena configuración para la mayoría de los problemas. Crea nuevas soluciones candidatas seleccionando soluciones aleatorias de la población, restando una de la otra y agregando una versión escalada de la diferencia a la mejor solución candidata en la población.
- nuevo = mejor + (mutación * (rand1 – rand2))
Los «popsizeEl argumento ”controla el tamaño o la cantidad de soluciones candidatas que se mantienen en la población. Es un factor del número de dimensiones en las soluciones candidatas y, por defecto, se establece en 15. Eso significa que para una función objetivo 2D que se mantendrá un tamaño de población de (2 * 15) o 30 soluciones candidatas.
El número total de iteraciones del algoritmo se mantiene mediante el «maxiter”Argumento y el valor predeterminado es 1.000.
Los «mutaciónEl argumento ”controla el número de cambios realizados en las soluciones candidatas en cada iteración. De forma predeterminada, se establece en 0,5. La cantidad de recombinación se controla mediante el «recombinación”, Que se establece en 0,7 (70 por ciento de una solución candidata dada) de forma predeterminada.
Finalmente, se aplica una búsqueda local a la mejor solución candidata que se encuentra al final de la búsqueda. Esto se controla mediante el «polaco”Argumento, que de forma predeterminada se establece en True.
El resultado de la búsqueda es un objeto OptimizeResult al que se puede acceder a las propiedades como un diccionario. Se puede acceder al éxito (o no) de la búsqueda a través de «éxito‘ o ‘mensaje‘ llave.
Se puede acceder al número total de evaluaciones de funciones a través de «nfev«Y se puede acceder a la entrada óptima encontrada para la búsqueda a través de»X‘ llave.
Ahora que estamos familiarizados con la API de evolución diferencial en Python, veamos algunos ejemplos prácticos.
Ejemplo resuelto de evolución diferencial
En esta sección, veremos un ejemplo del uso del algoritmo de evolución diferencial en una función objetiva desafiante.
La función de Ackley es un ejemplo de una función objetivo que tiene un único óptimo global y múltiples óptimos locales en los que una búsqueda local puede atascarse.
Como tal, se requiere una técnica de optimización global. Es una función objetivo bidimensional que tiene un óptimo global en [0,0], que se evalúa como 0.0.
El siguiente ejemplo implementa el Ackley y crea un gráfico de superficie tridimensional que muestra los óptimos globales y múltiples óptimos locales.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 dieciséis 17 18 19 20 21 22 23 24 25 26 27 28 29 30 |
# función multimodal ackley desde numpy importar arange desde numpy importar Exp desde numpy importar sqrt desde numpy importar porque desde numpy importar mi desde numpy importar Pi desde numpy importar rejilla desde matplotlib importar pyplot desde mpl_toolkits.mplot3d importar Ejes3D # función objetiva def objetivo(X, y): regreso –20,0 * Exp(–0,2 * sqrt(0,5 * (X**2 + y **2))) – Exp(0,5 * (porque(2 * Pi * X) + porque(2 * Pi * y))) + mi + 20 # definir rango para entrada r_min, r_max = –5,0, 5,0 # rango de entrada de muestra uniformemente en incrementos de 0.1 xaxis = arange(r_min, r_max, 0,1) yaxis = arange(r_min, r_max, 0,1) # crea una malla a partir del eje X, y = rejilla(xaxis, yaxis) # calcular objetivos resultados = objetivo(X, y) # crea un gráfico de superficie con el esquema de color jet figura = pyplot.figura() eje = figura.gca(proyección=‘3d’) eje.plot_surface(X, y, resultados, cmap=‘chorro’) # mostrar la trama pyplot.show() |
La ejecución del ejemplo crea el gráfico de superficie de la función Ackley que muestra la gran cantidad de óptimos locales.
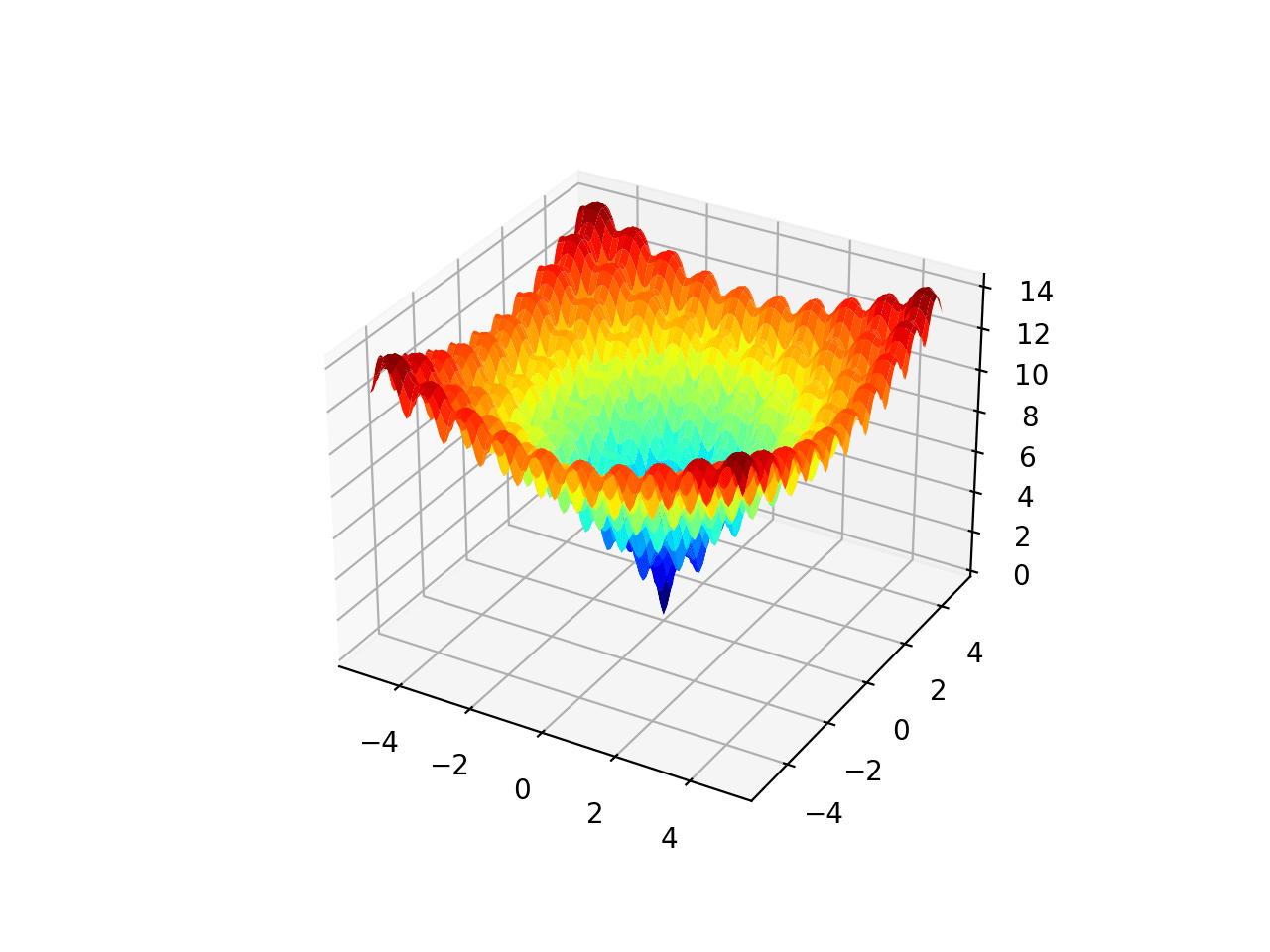
Gráfico de superficie 3D de la función multimodal de Ackley
Podemos aplicar el algoritmo de evolución diferencial a la función objetivo de Ackley.
Primero, podemos definir los límites del espacio de búsqueda como los límites de la función en cada dimensión.
|
... # definir los límites de la búsqueda límites = [[[[r_min, r_max], [[r_min, r_max]] |
Luego podemos aplicar la búsqueda especificando el nombre de la función objetivo y los límites de la búsqueda. En este caso, usaremos los hiperparámetros predeterminados.
|
... # realizar la búsqueda de evolución diferencial resultado = evolución_diferencial(objetivo, límites) |
Una vez completada la búsqueda, informará el estado de la búsqueda y el número de iteraciones realizadas, así como el mejor resultado encontrado con su evaluación.
|
... # resumir el resultado imprimir(‘Estado:% s’ % resultado[[‘mensaje’]) imprimir(‘Total de evaluaciones:% d’ % resultado[[‘nfev’]) # evaluar la solución solución = resultado[[‘X’] evaluación = objetivo(solución) imprimir(‘Solución: f (% s) =% .5f’ % (solución, evaluación)) |
Al unir esto, el ejemplo completo de aplicación de la evolución diferencial a la función objetivo de Ackley se enumera a continuación.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 dieciséis 17 18 19 20 21 22 23 24 25 26 27 |
# optimización global de evolución diferencial para la función objetivo multimodal de ackley desde scipy.optimizar importar evolución_diferencial desde numpy.aleatorio importar rand desde numpy importar Exp desde numpy importar sqrt desde numpy importar porque desde numpy importar mi desde numpy importar Pi # función objetiva def objetivo(v): X, y = v regreso –20,0 * Exp(–0,2 * sqrt(0,5 * (X**2 + y **2))) – Exp(0,5 * (porque(2 * Pi * X) + porque(2 * Pi * y))) + mi + 20 # definir rango para entrada r_min, r_max = –5,0, 5,0 # definir los límites de la búsqueda límites = [[[[r_min, r_max], [[r_min, r_max]] # realizar la búsqueda de evolución diferencial resultado = evolución_diferencial(objetivo, límites) # resumir el resultado imprimir(‘Estado:% s’ % resultado[[‘mensaje’]) imprimir(‘Total de evaluaciones:% d’ % resultado[[‘nfev’]) # evaluar la solución solución = resultado[[‘X’] evaluación = objetivo(solución) imprimir(‘Solución: f (% s) =% .5f’ % (solución, evaluación)) |
La ejecución del ejemplo ejecuta la optimización y luego informa los resultados.
Nota: Sus resultados pueden variar dada la naturaleza estocástica del algoritmo o procedimiento de evaluación, o las diferencias en la precisión numérica. Considere ejecutar el ejemplo varias veces y compare el resultado promedio.
En este caso, podemos ver que el algoritmo ubicó el óptimo con entradas iguales a cero y una evaluación de la función objetivo que es igual a cero.
Podemos ver que se realizaron un total de 3,063 evaluaciones de funciones.
|
Estado: la optimización finalizó con éxito. Total de valoraciones: 3063 Solución: f ([0. 0.]) = 0,00000 |
Otras lecturas
Esta sección proporciona más recursos sobre el tema si desea profundizar.
Documentos
Libros
API
Artículos
Resumen
En este tutorial, descubrió el algoritmo de optimización global de Evolución diferencial.
Específicamente, aprendiste:
- La optimización de la evolución diferencial es un tipo de algoritmo evolutivo que está diseñado para trabajar con soluciones candidatas de valor real.
- Cómo utilizar la API del algoritmo de optimización de Evolución Diferencial en Python.
- Ejemplos de uso de la evolución diferencial para resolver problemas de optimización global con múltiples óptimos.
¿Tiene usted alguna pregunta?
Haga sus preguntas en los comentarios a continuación y haré todo lo posible para responder.
