El descenso de gradiente es un algoritmo de optimización que sigue el gradiente negativo de una función objetivo para localizar el mínimo de la función.
Una limitación del descenso de gradiente es que el progreso de la búsqueda puede ralentizarse si el gradiente se vuelve plano o con una gran curvatura. Se puede agregar impulso al descenso de gradiente que incorpora cierta inercia a las actualizaciones. Esto se puede mejorar aún más incorporando el gradiente de la nueva posición proyectada en lugar de la posición actual, llamado Gradiente Acelerado de Nesterov (NAG) o impulso de Nesterov.
Otra limitación del descenso de gradiente es que se utiliza un tamaño de paso único (tasa de aprendizaje) para todas las variables de entrada. Extensiones al descenso de gradiente como el algoritmo Adaptive Movement Estimation (Adam) que usa un tamaño de paso separado para cada variable de entrada, pero puede resultar en un tamaño de paso que rápidamente disminuye a valores muy pequeños.
Estimación de momento adaptativo acelerada por Nesterov, o la Nadam, es una extensión del algoritmo de Adam que incorpora el impulso de Nesterov y puede resultar en un mejor rendimiento del algoritmo de optimización.
En este tutorial, descubrirá cómo desarrollar la optimización del descenso de gradientes con Nadam desde cero.
Después de completar este tutorial, sabrá:
- El descenso de gradiente es un algoritmo de optimización que utiliza el gradiente de la función objetivo para navegar por el espacio de búsqueda.
- Nadam es una extensión de la versión Adam del descenso en pendiente que incorpora el impulso de Nesterov.
- Cómo implementar el algoritmo de optimización de Nadam desde cero y aplicarlo a una función objetivo y evaluar los resultados.
Empecemos.

Optimización del descenso de gradientes con Nadam desde cero
Foto de BLM Nevada, algunos derechos reservados.
Descripción general del tutorial
Este tutorial se divide en tres partes; son:
- Descenso de gradiente
- Algoritmo de optimización de Nadam
- Descenso en gradiente con Nadam
- Problema de prueba bidimensional
- Optimización del descenso de gradientes con Nadam
- Visualización de la optimización de Nadam
Descenso de gradiente
El descenso de gradientes es un algoritmo de optimización.
Técnicamente se le conoce como un algoritmo de optimización de primer orden, ya que hace uso explícito de la derivada de primer orden de la función objetivo de destino.
Los métodos de primer orden se basan en la información del gradiente para ayudar a dirigir la búsqueda de un mínimo …
– Página 69, Algoritmos de optimización, 2019.
La derivada de primer orden, o simplemente la «derivada», es la tasa de cambio o pendiente de la función objetivo en un punto específico, p. Ej. para una entrada específica.
Si la función de destino toma múltiples variables de entrada, se denomina función multivariante y las variables de entrada se pueden considerar como un vector. A su vez, la derivada de una función objetivo multivariante también puede tomarse como un vector y se denomina generalmente gradiente.
- Degradado: Derivada de primer orden para una función objetivo multivariante.
La derivada o el gradiente apunta en la dirección del ascenso más pronunciado de la función de destino para una entrada específica.
El descenso de gradiente se refiere a un algoritmo de optimización de minimización que sigue el negativo del gradiente cuesta abajo de la función objetivo para localizar el mínimo de la función.
El algoritmo de descenso de gradiente requiere una función objetivo que se está optimizando y la función derivada para la función objetivo. La función objetivo F() devuelve una puntuación para un conjunto dado de entradas y la función derivada F'() da la derivada de la función objetivo para un conjunto dado de entradas.
El algoritmo de descenso de gradiente requiere un punto de partida (X) en el problema, como un punto seleccionado al azar en el espacio de entrada.
Luego se calcula la derivada y se da un paso en el espacio de entrada que se espera que resulte en un movimiento cuesta abajo en la función objetivo, asumiendo que estamos minimizando la función objetivo.
Un movimiento cuesta abajo se realiza calculando primero qué tan lejos moverse en el espacio de entrada, calculado como el tamaño de los pasos (llamado alfa o tasa de aprendizaje) multiplicado por el gradiente. Esto luego se resta del punto actual, asegurando que nos movemos contra el gradiente o hacia abajo de la función de destino.
- x
Cuanto más pronunciada sea la función objetivo en un punto dado, mayor será la magnitud del gradiente y, a su vez, mayor será el paso dado en el espacio de búsqueda. El tamaño del paso realizado se escala mediante un hiperparámetro de tamaño de paso.
- Numero de pie: Hiperparámetro que controla qué tan lejos moverse en el espacio de búsqueda contra el gradiente en cada iteración del algoritmo.
Si el tamaño del paso es demasiado pequeño, el movimiento en el espacio de búsqueda será pequeño y la búsqueda llevará mucho tiempo. Si el tamaño del paso es demasiado grande, la búsqueda puede rebotar en el espacio de búsqueda y omitir los óptimos.
Ahora que estamos familiarizados con el algoritmo de optimización del descenso de gradientes, echemos un vistazo al algoritmo de Nadam.
Algoritmo de optimización de Nadam
La estimación del momento adaptativo acelerada por Nesterov, o la Nadam, el algoritmo es una extensión del algoritmo de optimización Adaptive Movement Estimation (Adam) para agregar el gradiente acelerado de Nesterov (NAG) o el impulso de Nesterov, que es un tipo mejorado de impulso.
En términos más generales, el algoritmo Nadam es una extensión del algoritmo Gradient Descent Optimization.
El algoritmo fue descrito en el artículo de 2016 por Timothy Dozat titulado «Incorporando el impulso de Nesterov en Adam». Aunque una versión del documento se redactó en 2015 como un informe del proyecto de Stanford con el mismo nombre.
Momentum agrega un promedio móvil en declive exponencial (primer momento) del gradiente al algoritmo de descenso del gradiente. Esto tiene el impacto de suavizar las funciones objetivas ruidosas y mejorar la convergencia.
Adam es una extensión del descenso de gradiente que agrega un primer y segundo momento del gradiente y adapta automáticamente una tasa de aprendizaje para cada parámetro que se optimiza. NAG es una extensión del impulso en el que la actualización se realiza utilizando el gradiente de la actualización proyectada del parámetro en lugar del valor de la variable actual real. Esto tiene el efecto de ralentizar la búsqueda cuando se encuentra el óptimo en lugar de sobrepasar, en algunas situaciones.
Nadam es una extensión de Adam que usa el impulso NAG en lugar del impulso clásico.
Mostramos cómo modificar el componente de impulso de Adam para aprovechar los conocimientos de NAG, y luego presentamos evidencia preliminar que sugiere que hacer esta sustitución mejora la velocidad de convergencia y la calidad de los modelos aprendidos.
– Incorporación de Nesterov Momentum en Adam, 2016.
Repasemos cada elemento del algoritmo.
Nadam usa un tamaño de paso en descomposición (alfa) y primer momento (mu) hiperparámetros que pueden mejorar el rendimiento. Por simplicidad, ignoraremos este aspecto por ahora y asumiremos valores constantes.
Primero, debemos mantener el primer y segundo momento del gradiente para cada parámetro que se optimiza como parte de la búsqueda, lo que se conoce como metro y norte respectivamente. Se inicializan a 0.0 al comienzo de la búsqueda.
El algoritmo se ejecuta iterativamente a lo largo del tiempo t comenzando en t = 1, y cada iteración implica calcular un nuevo conjunto de valores de parámetros X, p.ej. ir desde x (t-1) a x
Quizás sea fácil entender el algoritmo si nos enfocamos en actualizar un parámetro, que se generaliza para actualizar todos los parámetros a través de operaciones vectoriales.
Primero, se calcula el gradiente (derivadas parciales) para el intervalo de tiempo actual.
A continuación, se actualiza el primer momento mediante el degradado y un hiperparámetro «mu“.
- m
Luego, el segundo momento se actualiza usando el «nu”Hiperparámetro.
- n
A continuación, se corrige el sesgo del primer momento utilizando el impulso de Nesterov.
- mhat = (mu * m
A continuación, se corrige el sesgo del segundo momento.
Nota: la corrección de sesgo es un aspecto de Adam y contrarresta el hecho de que el primer y segundo momento se inicializan a cero al comienzo de la búsqueda.
- nhat = nu * n
Finalmente, podemos calcular el valor del parámetro para esta iteración.
- x
Donde alfa es el hiperparámetro del tamaño del paso (tasa de aprendizaje), sqrt () es la función raíz cuadrada, y eps (épsilon) es un valor pequeño como 1e-8 agregado para evitar un error de división por cero.
Para revisar, hay tres hiperparámetros para el algoritmo; son:
- alfa: Tamaño del paso inicial (tasa de aprendizaje), un valor típico es 0,002.
- mu: Factor de decaimiento para el primer momento (beta1 en Adam), un valor típico es 0,975.
- nu: Factor de decaimiento por segundo momento (beta2 en Adam), un valor típico es 0,999.
Y eso es.
A continuación, veamos cómo podríamos implementar el algoritmo desde cero en Python.
Descenso en gradiente con Nadam
En esta sección, exploraremos cómo implementar el algoritmo de optimización del descenso de gradientes con Nadam Momentum.
Problema de prueba bidimensional
Primero, definamos una función de optimización.
Usaremos una función bidimensional simple que eleva al cuadrado la entrada de cada dimensión y define el rango de entradas válidas de -1.0 a 1.0.
los objetivo() función a continuación implementa esta función
|
# función objetiva def objetivo(X, y): regreso X**2.0 + y **2.0 |
Podemos crear una gráfica tridimensional del conjunto de datos para tener una idea de la curvatura de la superficie de respuesta.
El ejemplo completo de trazado de la función objetivo se enumera a continuación.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 dieciséis 17 18 19 20 21 22 23 24 |
# Gráfico 3d de la función de prueba desde numpy importar arange desde numpy importar rejilla desde matplotlib importar pyplot # función objetiva def objetivo(X, y): regreso X**2.0 + y **2.0 # definir rango para entrada r_min, r_max = –1.0, 1.0 # rango de entrada de muestra uniformemente en incrementos de 0.1 xaxis = arange(r_min, r_max, 0,1) yaxis = arange(r_min, r_max, 0,1) # crea una malla a partir del eje X, y = rejilla(xaxis, yaxis) # calcular objetivos resultados = objetivo(X, y) # crea un gráfico de superficie con el esquema de color jet figura = pyplot.figura() eje = figura.gca(proyección=‘3d’) eje.plot_surface(X, y, resultados, cmap=‘chorro’) # mostrar la trama pyplot.show() |
La ejecución del ejemplo crea un gráfico de superficie tridimensional de la función objetivo.
Podemos ver la forma familiar de cuenco con los mínimos globales en f (0, 0) = 0.
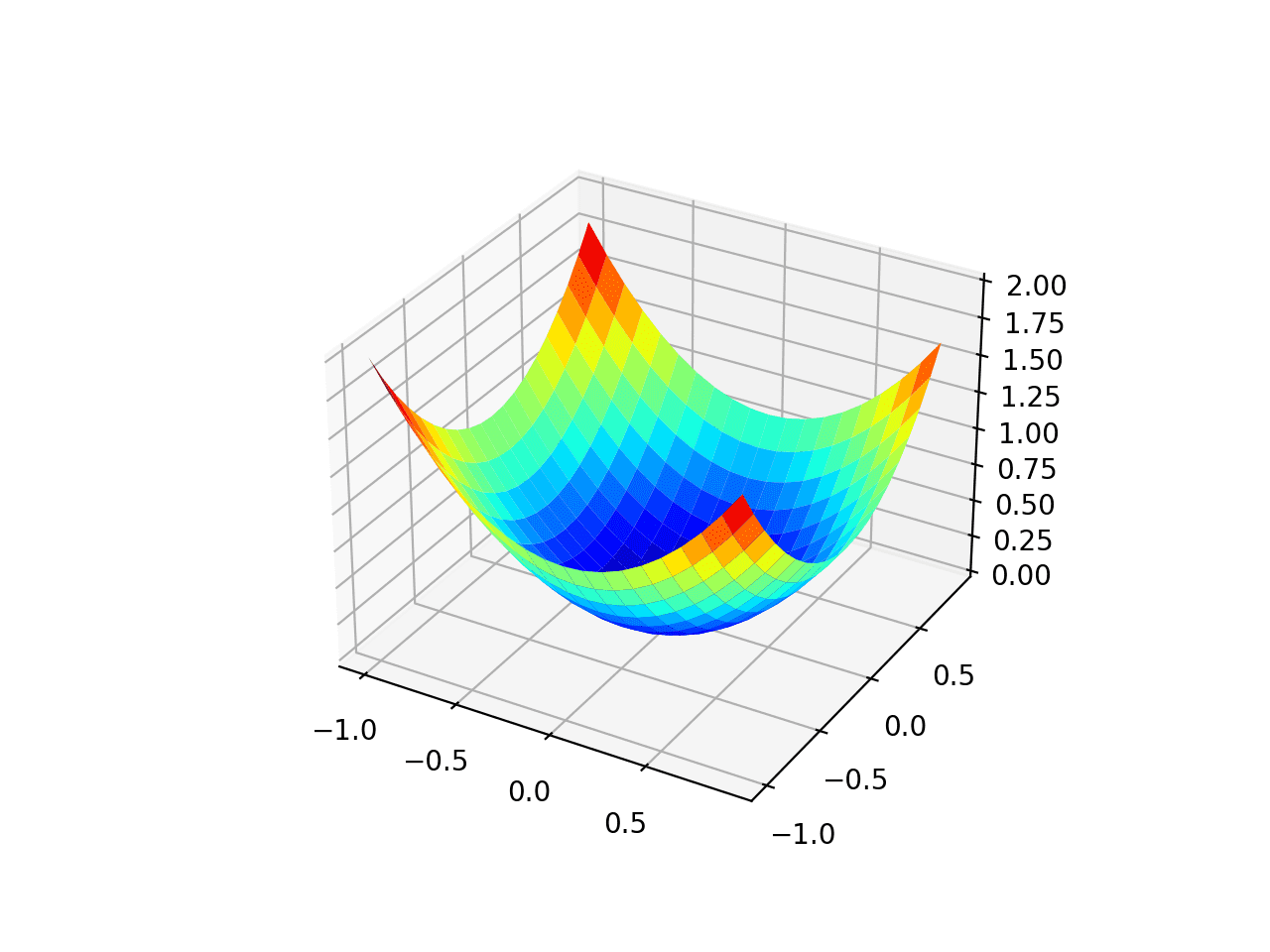
Gráfico tridimensional de la función objetivo de prueba
También podemos crear una gráfica bidimensional de la función. Esto será útil más adelante cuando queramos trazar el progreso de la búsqueda.
El siguiente ejemplo crea un gráfico de contorno de la función objetivo.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 dieciséis 17 18 19 20 21 22 23 |
# gráfica de contorno de la función de prueba desde numpy importar asarray desde numpy importar arange desde numpy importar rejilla desde matplotlib importar pyplot # función objetiva def objetivo(X, y): regreso X**2.0 + y **2.0 # definir rango para entrada límites = asarray([[[[–1.0, 1.0], [[–1.0, 1.0]]) # rango de entrada de muestra uniformemente en incrementos de 0.1 xaxis = arange(límites[[0,0], límites[[0,1], 0,1) yaxis = arange(límites[[1,0], límites[[1,1], 0,1) # crea una malla a partir del eje X, y = rejilla(xaxis, yaxis) # calcular objetivos resultados = objetivo(X, y) # crear un gráfico de contorno relleno con 50 niveles y esquema de color jet pyplot.contourf(X, y, resultados, niveles=50, cmap=‘chorro’) # mostrar la trama pyplot.show() |
La ejecución del ejemplo crea un gráfico de contorno bidimensional de la función objetivo.
Podemos ver la forma del cuenco comprimida a los contornos mostrados con un degradado de color. Usaremos este gráfico para trazar los puntos específicos explorados durante el progreso de la búsqueda.
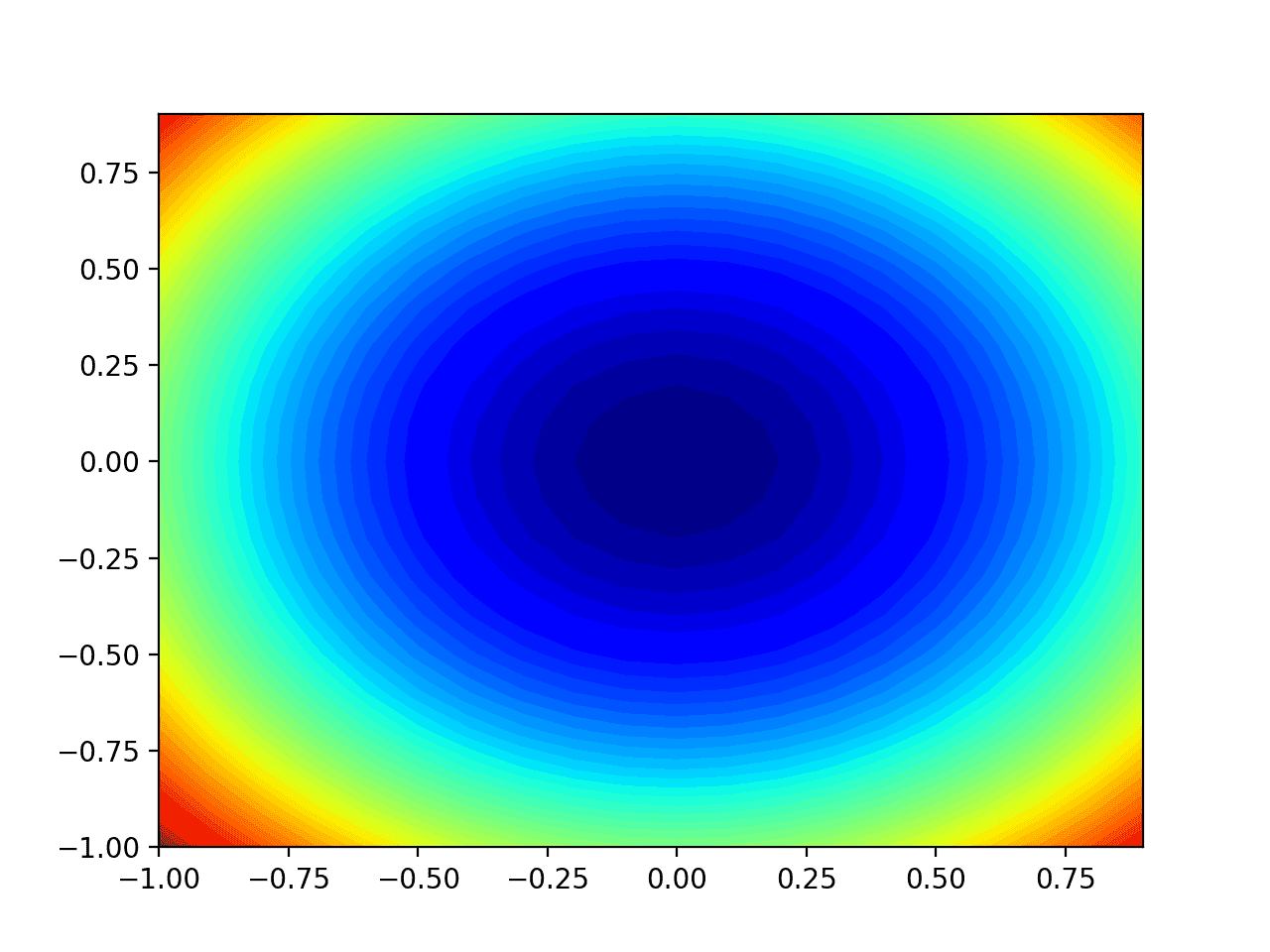
Gráfico de contorno bidimensional de la función objetivo de prueba
Ahora que tenemos una función de objetivo de prueba, veamos cómo podríamos implementar el algoritmo de optimización de Nadam.
Optimización del descenso de gradientes con Nadam
Podemos aplicar el descenso de gradiente con Nadam al problema de prueba.
Primero, necesitamos una función que calcule la derivada de esta función.
La derivada de x ^ 2 es x * 2 en cada dimensión.
La función derivada () implementa esto a continuación.
|
# derivada de la función objetivo def derivado(X, y): regreso asarray([[X * 2.0, y * 2.0]) |
A continuación, podemos implementar la optimización del descenso de gradientes con Nadam.
Primero, podemos seleccionar un punto aleatorio en los límites del problema como punto de partida para la búsqueda.
Esto supone que tenemos una matriz que define los límites de la búsqueda con una fila para cada dimensión y la primera columna define el mínimo y la segunda columna define el máximo de la dimensión.
|
... # generar un punto inicial X = límites[[:, 0] + rand(len(límites)) * (límites[[:, 1] – límites[[:, 0]) puntaje = objetivo(X[[0], X[[1]) |
A continuación, necesitamos inicializar los vectores de momento.
|
... # inicializar promedios móviles decrecientes metro = [[0.0 por _ en abarcar(límites.forma[[0])] norte = [[0.0 por _ en abarcar(límites.forma[[0])] |
Luego ejecutamos un número fijo de iteraciones del algoritmo definido por el «nitro”Hiperparámetro.
|
... # ejecutar iteraciones de descenso de gradiente por t en abarcar(nitro): ... |
El primer paso es calcular la derivada del conjunto de parámetros actual.
|
... # calcular gradiente g |
A continuación, debemos realizar los cálculos de actualización de Nadam. Realizaremos estos cálculos una variable a la vez utilizando un estilo de programación imperativo para facilitar la lectura.
En la práctica, recomiendo usar operaciones vectoriales NumPy para mayor eficiencia.
|
... # construye una solución una variable a la vez por I en abarcar(X.forma[[0]): ... |
Primero, necesitamos calcular el vector de momento.
|
... # m |
Luego, el segundo vector de momento.
|
... # norte |
Luego, el impulso de Nesterov corregido por sesgos.
|
... # mhat = (mu * m |
El segundo momento de corrección de sesgo.
|
... # nhat = nu * n |
Y finalmente actualizando el parámetro.
|
... # x |
Luego, esto se repite para cada parámetro que se está optimizando.
Al final de la iteración, podemos evaluar los nuevos valores de los parámetros e informar el rendimiento de la búsqueda.
|
... # evaluar el punto candidato puntaje = objetivo(X[[0], X[[1]) # informe de progreso imprimir(‘>% d f (% s) =% .5f’ % (t, X, puntaje)) |
Podemos unir todo esto en una función llamada nadam () que toma los nombres de las funciones objetivo y derivada, así como los hiperparámetros del algoritmo, y devuelve la mejor solución encontrada al final de la búsqueda y su evaluación.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 dieciséis 17 18 19 20 21 22 23 24 25 26 27 28 29 |
# algoritmo de descenso de gradiente con nadam def nadam(objetivo, derivado, límites, nitro, alfa, mu, nu, eps=1e–8): # generar un punto inicial X = límites[[:, 0] + rand(len(límites)) * (límites[[:, 1] – límites[[:, 0]) puntaje = objetivo(X[[0], X[[1]) # inicializar promedios móviles decrecientes metro = [[0.0 por _ en abarcar(límites.forma[[0])] norte = [[0.0 por _ en abarcar(límites.forma[[0])] # ejecutar el descenso de gradiente por t en abarcar(nitro): # calcular gradiente g |
Luego podemos definir los límites de la función y los hiperparámetros y llamar a la función para realizar la optimización.
En este caso, ejecutaremos el algoritmo para 50 iteraciones con un alfa inicial de 0.02, mu de 0.8 y un nu de 0.999, que se encuentran después de una pequeña prueba y error.
|
... # siembra el generador de números pseudoaleatorios semilla(1) # definir rango para entrada límites = asarray([[[[–1.0, 1.0], [[–1.0, 1.0]]) # definir las iteraciones totales nitro = 50 # tamaño de pasos alfa = 0,02 # factor de gradiente promedio mu = 0,8 # factor de gradiente cuadrático medio nu = 0,999 # realizar la búsqueda de descenso de gradiente con nadam mejor, puntaje = nadam(objetivo, derivado, límites, nitro, alfa, mu, nu) |
Al final de la ejecución, informaremos sobre la mejor solución encontrada.
|
... # resumir el resultado imprimir(‘¡Hecho!’) imprimir(‘f (% s) =% f’ % (mejor, puntaje)) |
Uniendo todo esto, el ejemplo completo del descenso de gradiente de Nadam aplicado a nuestro problema de prueba se enumera a continuación.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 dieciséis 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 |
# optimización del descenso de gradiente con nadam para una función de prueba bidimensional desde Matemáticas importar sqrt desde numpy importar asarray desde numpy.aleatorio importar rand desde numpy.aleatorio importar semilla # función objetiva def objetivo(X, y): regreso X**2.0 + y **2.0 # derivada de la función objetivo def derivado(X, y): regreso asarray([[X * 2.0, y * 2.0]) # algoritmo de descenso de gradiente con nadam def nadam(objetivo, derivado, límites, nitro, alfa, mu, nu, eps=1e–8): # generate an initial point X = bounds[[:, 0] + rand(len(bounds)) * (bounds[[:, 1] – bounds[[:, 0]) puntaje = objetivo(X[[0], X[[1]) # initialize decaying moving averages metro = [[0.0 por _ en abarcar(bounds.forma[[0])] norte = [[0.0 por _ en abarcar(bounds.forma[[0])] # run the gradient descent por t en abarcar(n_iter): # calculate gradient g |
Running the example applies the optimization algorithm with Nadam to our test problem and reports the performance of the search for each iteration of the algorithm.
Nota: Your results may vary given the stochastic nature of the algorithm or evaluation procedure, or differences in numerical precision. Consider running the example a few times and compare the average outcome.
In this case, we can see that a near-optimal solution was found after perhaps 44 iterations of the search, with input values near 0.0 and 0.0, evaluating to 0.0.
|
… >40 f([ 5.07445337e-05 -3.32910019e-03]) = 0.00001 >41 f([-1.84325171e-05 -3.00939427e-03]) = 0.00001 >42 f([-6.78814472e-05 -2.69839367e-03]) = 0.00001 >43 f([-9.88339249e-05 -2.40042096e-03]) = 0.00001 >44 f([-0.00011368 -0.00211861]) = 0.00000 >45 f([-0.00011547 -0.00185511]) = 0.00000 >46 f([-0.0001075 -0.00161122]) = 0.00000 >47 f([-9.29922627e-05 -1.38760991e-03]) = 0.00000 >48 f([-7.48258406e-05 -1.18436586e-03]) = 0.00000 >49 f([-5.54299505e-05 -1.00116899e-03]) = 0.00000 Done! f([-5.54299505e-05 -1.00116899e-03]) = 0.000001 |
Visualization of Nadam Optimization
We can plot the progress of the Nadam search on a contour plot of the domain.
This can provide an intuition for the progress of the search over the iterations of the algorithm.
We must update the nadam() function to maintain a list of all solutions found during the search, then return this list at the end of the search.
The updated version of the function with these changes is listed below.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 dieciséis 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 |
# gradient descent algorithm with nadam def nadam(objetivo, derivative, bounds, n_iter, alpha, mu, nu, eps=1e–8): solutions = lista() # generate an initial point X = bounds[[:, 0] + rand(len(bounds)) * (bounds[[:, 1] – bounds[[:, 0]) puntaje = objetivo(X[[0], X[[1]) # initialize decaying moving averages metro = [[0.0 por _ en abarcar(bounds.forma[[0])] norte = [[0.0 por _ en abarcar(bounds.forma[[0])] # run the gradient descent por t en abarcar(n_iter): # calculate gradient g |
We can then execute the search as before, and this time retrieve the list of solutions instead of the best final solution.
|
... # seed the pseudo random number generator seed(1) # define range for input bounds = asarray([[[[–1.0, 1.0], [[–1.0, 1.0]]) # define the total iterations n_iter = 50 # steps size alpha = 0.02 # factor for average gradient mu = 0.8 # factor for average squared gradient nu = 0.999 # perform the gradient descent search with nadam solutions = nadam(objetivo, derivative, bounds, n_iter, alpha, mu, nu) |
We can then create a contour plot of the objective function, as before.
|
... # sample input range uniformly at 0.1 increments xaxis = arange(bounds[[0,0], bounds[[0,1], 0.1) yaxis = arange(bounds[[1,0], bounds[[1,1], 0.1) # create a mesh from the axis X, y = meshgrid(xaxis, yaxis) # compute targets results = objetivo(X, y) # create a filled contour plot with 50 levels and jet color scheme pyplot.contourf(X, y, results, niveles=50, cmap=‘jet’) |
Finally, we can plot each solution found during the search as a white dot connected by a line.
|
... # plot the sample as black circles solutions = asarray(solutions) pyplot.plot(solutions[[:, 0], solutions[[:, 1], ‘.-‘, color=‘w’) |
Tying this all together, the complete example of performing the Nadam optimization on the test problem and plotting the results on a contour plot is listed below.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 dieciséis 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 sesenta y cinco 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 |
# example of plotting the nadam search on a contour plot of the test function desde Matemáticas import sqrt desde numpy import asarray desde numpy import arange desde numpy import producto desde numpy.aleatorio import rand desde numpy.aleatorio import seed desde numpy import meshgrid desde matplotlib import pyplot desde mpl_toolkits.mplot3d import Axes3D # objective function def objetivo(X, y): regreso x**2.0 + y**2.0 # derivative of objective function def derivative(X, y): regreso asarray([[x * 2.0, y * 2.0]) # gradient descent algorithm with nadam def nadam(objetivo, derivative, bounds, n_iter, alpha, mu, nu, eps=1e–8): solutions = lista() # generate an initial point X = bounds[[:, 0] + rand(len(bounds)) * (bounds[[:, 1] – bounds[[:, 0]) puntaje = objetivo(X[[0], X[[1]) # initialize decaying moving averages metro = [[0.0 por _ en abarcar(bounds.forma[[0])] norte = [[0.0 por _ en abarcar(bounds.forma[[0])] # run the gradient descent por t en abarcar(n_iter): # calculate gradient g |
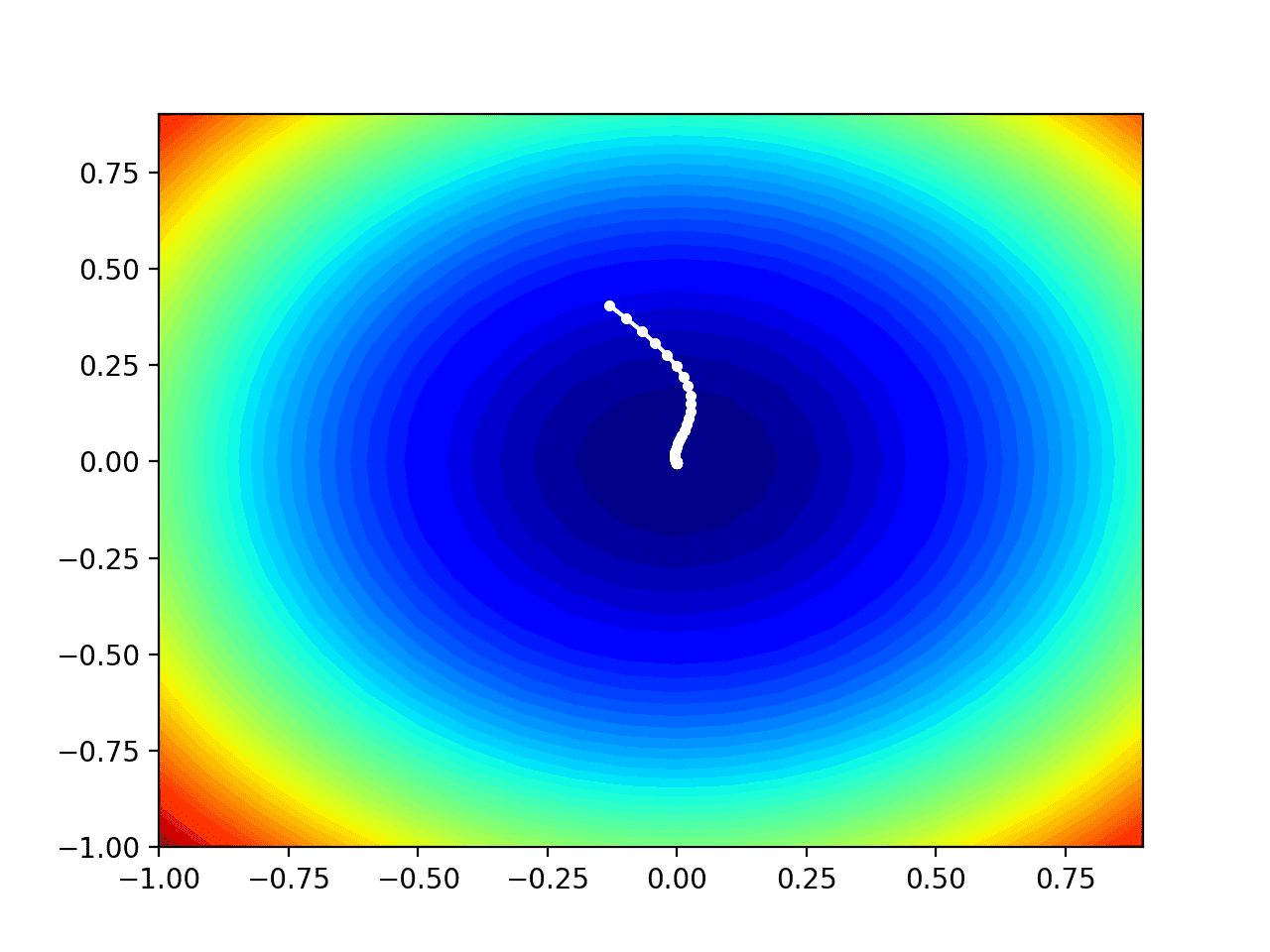
Running the example performs the search as before, except in this case, the contour plot of the objective function is created.
In this case, we can see that a white dot is shown for each solution found during the search, starting above the optima and progressively getting closer to the optima at the center of the plot.

Contour Plot of the Test Objective Function With Nadam Search Results Shown
Further Reading
This section provides more resources on the topic if you are looking to go deeper.
Papers
Books
APIs
Articles
Resumen
In this tutorial, you discovered how to develop the gradient descent optimization with Nadam from scratch.
Specifically, you learned:
- Gradient descent is an optimization algorithm that uses the gradient of the objective function to navigate the search space.
- Nadam is an extension of the Adam version of gradient descent that incorporates Nesterov momentum.
- How to implement the Nadam optimization algorithm from scratch and apply it to an objective function and evaluate the results.
Do you have any questions?
Ask your questions in the comments below and I will do my best to answer.
