Salto de cuenca es un algoritmo de optimización global.
Fue desarrollado para resolver problemas de física química, aunque es un algoritmo eficaz adecuado para funciones objetivas no lineales con múltiples óptimos.
En este tutorial, descubrirá el algoritmo de optimización global de salto de cuenca.
Después de completar este tutorial, sabrá:
- La optimización del salto de cuencas es una optimización global que utiliza perturbaciones aleatorias para saltar cuencas y un algoritmo de búsqueda local para optimizar cada cuenca.
- Cómo utilizar la API del algoritmo de optimización de salto de cuenca en Python.
- Ejemplos de uso de basin hopping para resolver problemas de optimización global con múltiples óptimos.
Empecemos.

Optimización de salto de cuenca en Python
Foto de Pedro Szekely, algunos derechos reservados.
Descripción general del tutorial
Este tutorial se divide en tres partes; son:
- Optimización del salto de cuencas
- API de salto de cuenca
- Ejemplos de saltos de cuencas
- Optimización multimodal con Optima local
- Optimización multimodal con múltiples óptimas globales
Optimización del salto de cuencas
Basin Hopping es un algoritmo de optimización global desarrollado para su uso en el campo de la física química.
Basin-Hopping (BH) o Minimización de Monte-Carlo (MCM) es hasta ahora los algoritmos más confiables en física química para buscar la estructura de menor energía de los cúmulos atómicos y sistemas macromoleculares.
– Basin Hopping con saltos ocasionales, 2004.
La optimización local se refiere a algoritmos de optimización destinados a localizar un óptimo para una función objetivo univariante u operar en una región donde se cree que está presente un óptimo. Mientras que los algoritmos de optimización global están destinados a localizar el único óptimo global entre potencialmente múltiples óptimos locales (no globales).
El salto de cuenca fue descrito por David Wales y Jonathan Doye en su artículo de 1997 titulado «Optimización global por salto de cuenca y las estructuras de energía más bajas de los clústeres de Lennard-Jones que contienen hasta 110 átomos».
Los algoritmos implican un ciclo de dos pasos, una perturbación de buenas soluciones candidatas y la aplicación de una búsqueda local a la solución perturbada.
[Basin hopping] transforma el complejo paisaje energético en una colección de cuencas y las explora saltando, lo que se logra mediante movimientos aleatorios de Montecarlo y aceptación / rechazo utilizando el criterio de Metropolis.
– Basin Hopping con saltos ocasionales, 2004.
La perturbación permite que el algoritmo de búsqueda salte a nuevas regiones del espacio de búsqueda y localice potencialmente una nueva cuenca que conduzca a un óptimo diferente, p. «saltos de cuencas”En el nombre de la técnica.
La búsqueda local permite al algoritmo atravesar la nueva cuenca hasta el óptimo.
El nuevo óptimo puede mantenerse como base para nuevas perturbaciones aleatorias, de lo contrario, se descarta. La decisión de mantener la nueva solución está controlada por una función de decisión estocástica con un «la temperatura”Variable, muy parecido al recocido simulado.
La temperatura se ajusta en función del número de iteraciones del algoritmo. Esto permite que se acepten soluciones arbitrarias al principio de la ejecución cuando la temperatura es alta, y una política más estricta de aceptar solo soluciones de mejor calidad más adelante en la búsqueda cuando la temperatura es baja.
De esta manera, el algoritmo es muy parecido a una búsqueda local iterada con diferentes puntos de partida (perturbados).
El algoritmo se ejecuta para un número específico de iteraciones o evaluaciones de funciones y se puede ejecutar varias veces para aumentar la confianza de que se ubicó el óptimo global o que se ubicó una solución relativamente buena.
Ahora que estamos familiarizados con el algoritmo de salto básico desde un nivel alto, veamos la API para el salto de cuenca en Python.
API de salto de cuenca
El salto de cuenca está disponible en Python a través de la función SciPy de basinhopping ().
La función toma el nombre de la función objetivo a minimizar y el punto de partida inicial.
|
... # realizar la búsqueda de saltos de cuencas resultado = basinhopping(objetivo, pt) |
Otro hiperparámetro importante es el número de iteraciones para ejecutar el conjunto de búsqueda mediante el «nitro”Argumento y el valor predeterminado es 100.
Esto se puede establecer en miles de iteraciones o más.
|
... # realizar la búsqueda de saltos de cuencas resultado = basinhopping(objetivo, pt, nitro=10000) |
La cantidad de perturbación aplicada a la solución candidata se puede controlar mediante el «Numero de pie”Que define la cantidad máxima de cambio aplicado en el contexto de los límites del dominio del problema. De forma predeterminada, se establece en 0.5, pero debe establecerse en algo razonable en el dominio que podría permitir que la búsqueda encuentre una nueva cuenca.
Por ejemplo, si los límites razonables de un espacio de búsqueda fueran de -100 a 100, entonces quizás sería apropiado un tamaño de paso de 5.0 o 10.0 unidades (por ejemplo, 2.5% o 5% del dominio).
|
... # realizar la búsqueda de saltos de cuencas resultado = basinhopping(objetivo, pt, Numero de pie=10.0) |
De forma predeterminada, el algoritmo de búsqueda local que se utiliza es el «L-BFGS-B”Algoritmo.
Esto se puede cambiar configurando el «minimizer_kwargs«Argumento a un directorio con una clave de»método«Y el valor como el nombre del algoritmo de búsqueda local que se utilizará, como»nelder-mead. » Se puede utilizar cualquiera de los algoritmos de búsqueda local proporcionados por la biblioteca SciPy.
|
... # realizar la búsqueda de saltos de cuencas resultado = basinhopping(objetivo, pt, minimizer_kwargs={‘método’:‘nelder-mead’}) |
El resultado de la búsqueda es un objeto OptimizeResult al que se puede acceder a las propiedades como un diccionario. Se puede acceder al éxito (o no) de la búsqueda a través de «éxito‘ o ‘mensaje‘ llave.
Se puede acceder al número total de evaluaciones de funciones a través de «nfev«Y se puede acceder a la entrada óptima encontrada para la búsqueda a través de»X‘ llave.
Ahora que estamos familiarizados con la API de salto de cuenca en Python, veamos algunos ejemplos prácticos.
Ejemplos de saltos de cuencas
En esta sección, veremos algunos ejemplos del uso del algoritmo de salto de cuenca en funciones objetivas multimodales.
Las funciones objetivo multimodales son aquellas que tienen múltiples óptimos, como un óptimo global y muchos óptimos locales, o múltiples óptimos globales con la misma salida de función objetivo.
Veremos ejemplos de salto de cuenca en ambas funciones.
Optimización multimodal con Optima local
La función de Ackley es un ejemplo de una función objetivo que tiene un único óptimo global y múltiples óptimos locales en los que una búsqueda local puede atascarse.
Como tal, se requiere una técnica de optimización global. Es una función objetivo bidimensional que tiene un óptimo global en [0,0], que se evalúa como 0.0.
El siguiente ejemplo implementa el Ackley y crea un gráfico de superficie tridimensional que muestra los óptimos globales y múltiples óptimos locales.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 dieciséis 17 18 19 20 21 22 23 24 25 26 27 28 29 30 |
# función multimodal ackley desde numpy importar arange desde numpy importar Exp desde numpy importar sqrt desde numpy importar porque desde numpy importar mi desde numpy importar Pi desde numpy importar rejilla desde matplotlib importar pyplot desde mpl_toolkits.mplot3d importar Ejes3D # función objetiva def objetivo(X, y): regreso –20,0 * Exp(–0,2 * sqrt(0,5 * (X**2 + y **2))) – Exp(0,5 * (porque(2 * Pi * X) + porque(2 * Pi * y))) + mi + 20 # definir rango para entrada r_min, r_max = –5,0, 5,0 # rango de entrada de muestra uniformemente en incrementos de 0.1 xaxis = arange(r_min, r_max, 0,1) yaxis = arange(r_min, r_max, 0,1) # crea una malla a partir del eje X, y = rejilla(xaxis, yaxis) # calcular objetivos resultados = objetivo(X, y) # crea un gráfico de superficie con el esquema de color jet figura = pyplot.figura() eje = figura.gca(proyección=‘3d’) eje.plot_surface(X, y, resultados, cmap=‘chorro’) # mostrar la trama pyplot.show() |
La ejecución del ejemplo crea el gráfico de superficie de la función Ackley que muestra la gran cantidad de óptimos locales.
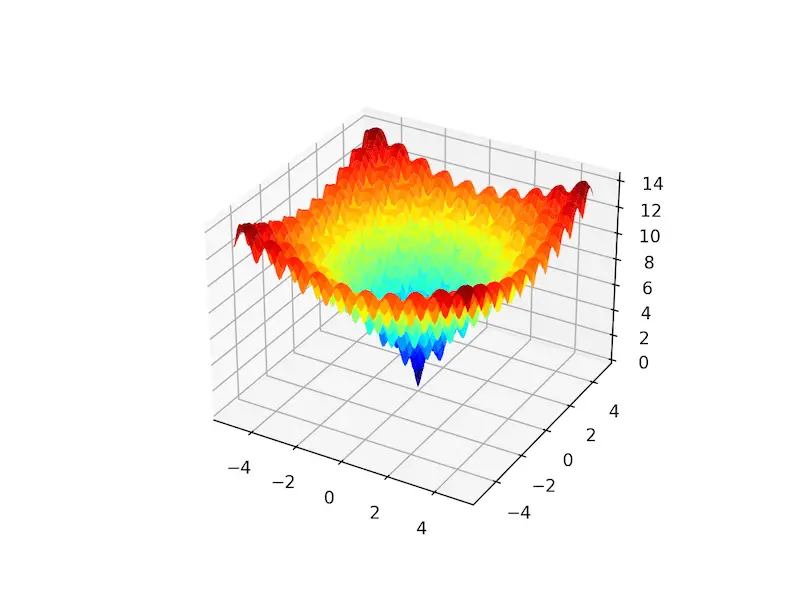
Gráfico de superficie 3D de la función multimodal de Ackley
Podemos aplicar el algoritmo de salto de cuencas a la función objetivo de Ackley.
En este caso, comenzaremos la búsqueda utilizando un punto aleatorio extraído del dominio de entrada entre -5 y 5.
|
... # definir el punto de partida como una muestra aleatoria del dominio pt = r_min + rand(2) * (r_max – r_min) |
Usaremos un tamaño de paso de 0.5, 200 iteraciones y el algoritmo de búsqueda local predeterminado. Esta configuración se eligió después de un poco de prueba y error.
|
... # realizar la búsqueda de saltos de cuencas resultado = basinhopping(objetivo, pt, Numero de pie=0,5, nitro=200) |
Una vez completada la búsqueda, informará el estado de la búsqueda y el número de iteraciones realizadas, así como el mejor resultado encontrado con su evaluación.
|
... # resumir el resultado imprimir(‘Estado:% s’ % resultado[[‘mensaje’]) imprimir(‘Total de evaluaciones:% d’ % resultado[[‘nfev’]) # evaluar la solución solución = resultado[[‘X’] evaluación = objetivo(solución) imprimir(‘Solución: f (% s) =% .5f’ % (solución, evaluación)) |
Al unir esto, el ejemplo completo de la aplicación del salto de cuenca a la función objetivo de Ackley se enumera a continuación.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 dieciséis 17 18 19 20 21 22 23 24 25 26 27 |
# optimización global de salto de cuenca para la función objetivo multimodal de ackley desde scipy.optimizar importar basinhopping desde numpy.aleatorio importar rand desde numpy importar Exp desde numpy importar sqrt desde numpy importar porque desde numpy importar mi desde numpy importar Pi # función objetiva def objetivo(v): X, y = v regreso –20,0 * Exp(–0,2 * sqrt(0,5 * (X**2 + y **2))) – Exp(0,5 * (porque(2 * Pi * X) + porque(2 * Pi * y))) + mi + 20 # definir rango para entrada r_min, r_max = –5,0, 5,0 # definir el punto de partida como una muestra aleatoria del dominio pt = r_min + rand(2) * (r_max – r_min) # realizar la búsqueda de saltos de cuencas resultado = basinhopping(objetivo, pt, Numero de pie=0,5, nitro=200) # resumir el resultado imprimir(‘Estado:% s’ % resultado[[‘mensaje’]) imprimir(‘Total de evaluaciones:% d’ % resultado[[‘nfev’]) # evaluar la solución solución = resultado[[‘X’] evaluación = objetivo(solución) imprimir(‘Solución: f (% s) =% .5f’ % (solución, evaluación)) |
La ejecución del ejemplo ejecuta la optimización y luego informa los resultados.
Nota: Sus resultados pueden variar dada la naturaleza estocástica del algoritmo o procedimiento de evaluación, o las diferencias en la precisión numérica. Considere ejecutar el ejemplo varias veces y compare el resultado promedio.
En este caso, podemos ver que el algoritmo ubicó los óptimos con entradas muy cercanas a cero y una evaluación de la función objetivo que es prácticamente cero.
Podemos ver que 200 iteraciones del algoritmo dieron como resultado 86 020 evaluaciones de funciones.
|
Estado: [‘requested number of basinhopping iterations completed successfully’] Total de valoraciones: 86020 Solución: f ([ 5.29778873e-10 -2.29022817e-10]) = 0,00000 |
Optimización multimodal con múltiples óptimas globales
La función Himmelblau es un ejemplo de una función objetivo que tiene múltiples óptimos globales.
Específicamente, tiene cuatro óptimos y cada uno tiene la misma evaluación de función objetivo. Es una función objetivo bidimensional que tiene un óptimo global en [3.0, 2.0], [-2.805118, 3.131312], [-3.779310, -3.283186], [3.584428, -1.848126].
Esto significa que cada ejecución de un algoritmo de optimización global puede encontrar un óptimo global diferente.
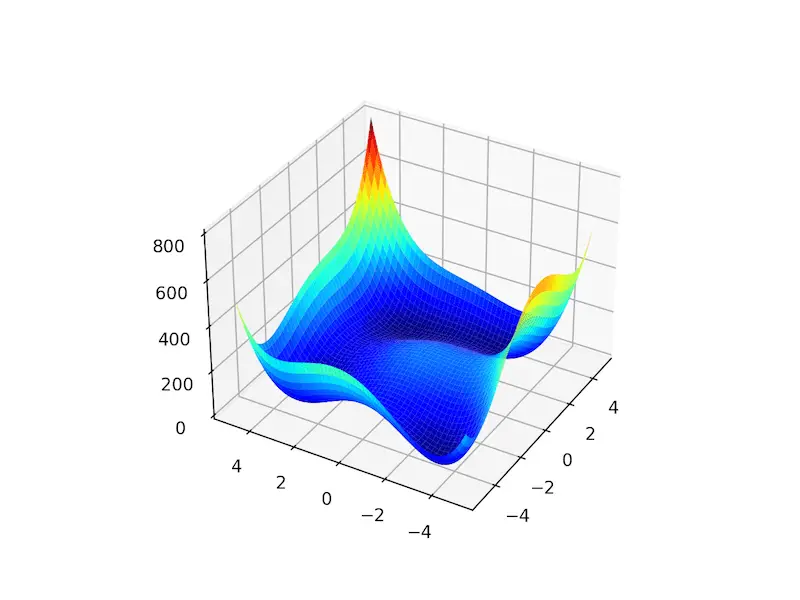
El siguiente ejemplo implementa el Himmelblau y crea un gráfico de superficie tridimensional para dar una intuición de la función objetivo.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 dieciséis 17 18 19 20 21 22 23 24 25 |
# función de prueba multimodal himmelblau desde numpy importar arange desde numpy importar rejilla desde matplotlib importar pyplot desde mpl_toolkits.mplot3d importar Ejes3D # función objetiva def objetivo(X, y): regreso (X**2 + y – 11)**2 + (X + y **2 –7)**2 # definir rango para entrada r_min, r_max = –5,0, 5,0 # rango de entrada de muestra uniformemente en incrementos de 0.1 xaxis = arange(r_min, r_max, 0,1) yaxis = arange(r_min, r_max, 0,1) # crea una malla a partir del eje X, y = rejilla(xaxis, yaxis) # calcular objetivos resultados = objetivo(X, y) # crea un gráfico de superficie con el esquema de color jet figura = pyplot.figura() eje = figura.gca(proyección=‘3d’) eje.plot_surface(X, y, resultados, cmap=‘chorro’) # mostrar la trama pyplot.show() |
La ejecución del ejemplo crea el gráfico de superficie de la función Himmelblau que muestra los cuatro óptimos globales como cuencas de color azul oscuro.

Gráfico de superficie 3D de la función multimodal Himmelblau
Podemos aplicar el algoritmo de salto de cuenca a la función objetivo de Himmelblau.
Como en el ejemplo anterior, comenzaremos la búsqueda usando un punto aleatorio extraído del dominio de entrada entre -5 y 5.
Usaremos un tamaño de paso de 0.5, 200 iteraciones y el algoritmo de búsqueda local predeterminado. Al final de la búsqueda, informaremos la entrada para los óptimos mejor ubicados,
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 dieciséis 17 18 19 20 21 22 |
# optimización global de salto de cuenca para la función objetivo multimodal himmelblau desde scipy.optimizar importar basinhopping desde numpy.aleatorio importar rand # función objetiva def objetivo(v): X, y = v regreso (X**2 + y – 11)**2 + (X + y **2 –7)**2 # definir rango para entrada r_min, r_max = –5,0, 5,0 # definir el punto de partida como una muestra aleatoria del dominio pt = r_min + rand(2) * (r_max – r_min) # realizar la búsqueda de saltos de cuencas resultado = basinhopping(objetivo, pt, Numero de pie=0,5, nitro=200) # resumir el resultado imprimir(‘Estado:% s’ % resultado[[‘mensaje’]) imprimir(‘Total de evaluaciones:% d’ % resultado[[‘nfev’]) # evaluar la solución solución = resultado[[‘X’] evaluación = objetivo(solución) imprimir(‘Solución: f (% s) =% .5f’ % (solución, evaluación)) |
La ejecución del ejemplo ejecuta la optimización y luego informa los resultados.
¿Quiere comenzar con el aprendizaje por conjuntos?
Realice ahora mi curso intensivo gratuito de 7 días por correo electrónico (con código de muestra).
Haga clic para registrarse y obtener también una versión gratuita en formato PDF del curso.
Descarga tu minicurso GRATIS
En este caso, podemos ver que el algoritmo ubicó un óptimo en aproximadamente [3.0, 2.0].
Podemos ver que 200 iteraciones del algoritmo dieron como resultado 7,660 evaluaciones de funciones.
|
Estado : [‘requested number of basinhopping iterations completed successfully’] Total de valoraciones: 7660 Solución: f ([3. 1.99999999]) = 0,00000 |
Si volvemos a ejecutar la búsqueda, podemos esperar que se localice un óptimo global diferente.
Por ejemplo, a continuación, podemos ver un óptimo ubicado en aproximadamente [-2.805118, 3.131312], diferente de la ejecución anterior.
|
Estado : [‘requested number of basinhopping iterations completed successfully’] Total de valoraciones: 7636 Solución: f ([-2.80511809 3.13131252]) = 0,00000 |
Otras lecturas
Esta sección proporciona más recursos sobre el tema si desea profundizar.
Documentos
Libros
API
Artículos
Resumen
En este tutorial, descubrió el algoritmo de optimización global de salto de cuenca.
Específicamente, aprendiste:
- La optimización del salto de cuencas es una optimización global que utiliza perturbaciones aleatorias para saltar cuencas y un algoritmo de búsqueda local para optimizar cada cuenca.
- Cómo utilizar la API del algoritmo de optimización de salto de cuenca en Python.
- Ejemplos de uso de basin hopping para resolver problemas de optimización global con múltiples óptimos.
¿Tiene usted alguna pregunta?
Haga sus preguntas en los comentarios a continuación y haré todo lo posible para responder.
