¿Cómo optimizar una función con una variable?
La optimización de funciones univariadas implica encontrar la entrada a una función que da como resultado la salida óptima de una función objetivo.
Este es un procedimiento común en el aprendizaje automático cuando se ajusta un modelo con un parámetro o se ajusta un modelo que tiene un solo hiperparámetro.
Se requiere un algoritmo eficiente para resolver problemas de optimización de este tipo que encontrará la mejor solución con el número mínimo de evaluaciones de la función objetivo, dado que cada evaluación de la función objetivo podría ser computacionalmente costosa, como ajustar y evaluar un modelo en un conjunto de datos.
Esto excluye la búsqueda de cuadrícula costosa y los algoritmos de búsqueda aleatoria y favorece algoritmos eficientes como el método de Brent.
En este tutorial, descubrirá cómo realizar la optimización de funciones univariadas en Python.
Después de completar este tutorial, sabrá:
- La optimización de funciones univariadas implica encontrar una entrada óptima para una función objetivo que toma un solo argumento continuo.
- Cómo realizar la optimización de una función univariante para una función convexa sin restricciones.
- Cómo realizar la optimización de una función univariante para una función no convexa sin restricciones.
Empecemos.

Optimización de funciones univariadas en Python
Foto de Robert Haandrikman, algunos derechos reservados.
Descripción general del tutorial
Este tutorial se divide en tres partes; son:
- Optimización de funciones univariadas
- Optimización de funciones univariadas convexas
- Optimización de funciones univariadas no convexas
Optimización de funciones univariadas
Es posible que necesitemos encontrar un valor óptimo de una función que tome un solo parámetro.
En el aprendizaje automático, esto puede ocurrir en muchas situaciones, como:
- Encontrar el coeficiente de un modelo para ajustarlo a un conjunto de datos de entrenamiento.
- Encontrar el valor de un solo hiperparámetro que da como resultado el mejor rendimiento del modelo.
Esto se llama optimización de función univariante.
Es posible que nos interese el resultado mínimo o el resultado máximo de la función, aunque esto se puede simplificar a la minimización, ya que una función maximizadora puede minimizarse agregando un signo negativo a todos los resultados de la función.
Puede haber o no límites en las entradas a la función, la llamada optimización no restringida o restringida, y asumimos que pequeños cambios en la entrada corresponden a pequeños cambios en la salida de la función, p. que es suave.
La función puede tener o no un solo optima, aunque preferimos que tenga un solo optima y que la forma de la función parezca un gran lavabo. Si este es el caso, sabemos que podemos muestrear la función en un punto y encontrar la ruta hasta los mínimos de la función. Técnicamente, esto se conoce como función convexa para minimizar (cóncava para maximizar), y las funciones que no tienen esta forma de cuenca se denominan no convexas.
- Función de objetivo convexo: Hay un único óptimo y la forma de la función objetivo conduce a este óptimo.
Sin embargo, la función objetivo es lo suficientemente compleja como para que no conozcamos la derivada, lo que significa que no podemos usar el cálculo para calcular analíticamente el mínimo o el máximo de la función donde el gradiente es cero. Esto se conoce como una función que no es diferenciable.
Aunque es posible que podamos muestrear la función con valores candidatos, no conocemos la entrada que dará como resultado el mejor resultado. Esto puede deberse a las muchas razones por las que resulta caro evaluar las soluciones candidatas.
Por lo tanto, necesitamos un algoritmo que muestree de manera eficiente los valores de entrada a la función.
Un enfoque para resolver problemas de optimización de funciones univariadas es utilizar el método de Brent.
El método de Brent es un algoritmo de optimización que combina un algoritmo de bisección (método de Dekker) y una interpolación cuadrática inversa. Se puede utilizar para la optimización de funciones univariadas restringidas y no restringidas.
El método Brent-Dekker es una extensión del método de bisección. Es un algoritmo de búsqueda de raíces que combina elementos del método secante y la interpolación cuadrática inversa. Tiene propiedades de convergencia confiables y rápidas, y es el algoritmo de optimización univariante de elección en muchos paquetes populares de optimización numérica.
– Páginas 49-51, Algoritmos de optimización, 2019.
Los algoritmos de bisección utilizan un paréntesis (inferior y superior) de valores de entrada y dividen el dominio de entrada, dividiéndolo en dos para localizar en qué parte del dominio se encuentra el óptimo, de forma muy similar a una búsqueda binaria. El método de Dekker es una de las formas en que esto se logra de manera eficiente para un dominio continuo.
El método de Dekker se atasca en problemas no convexos. El método de Brent modifica el método de Dekker para evitar quedarse atascado y también se aproxima a la segunda derivada de la función objetivo (llamado método secante) en un esfuerzo por acelerar la búsqueda.
Como tal, el método de Brent para la optimización de funciones univariadas generalmente se prefiere sobre la mayoría de los otros algoritmos de optimización de funciones univariantes dada su eficiencia.
El método de Brent está disponible en Python a través de la función de SciPy minimizar_scalar () que toma el nombre de la función a minimizar. Si su función de destino está restringida a un rango, se puede especificar mediante el «límites» argumento.
Devuelve un objeto OptimizeResult que es un diccionario que contiene la solución. Es importante destacar que el «X«Clave resume la entrada para el optima, el»divertidoLa tecla «resume la salida de la función para los óptimos, y la tecla»nfev‘Resume el número de evaluaciones de la función objetivo que se realizaron.
|
... # minimizar la función resultado = minimizar_escalar(objetivo, método=‘brent’) |
Ahora que sabemos cómo realizar la optimización de funciones univariadas en Python, veamos algunos ejemplos.
Optimización de funciones univariadas convexas
En esta sección, exploraremos cómo resolver un problema de optimización de función univariante convexa.
Primero, podemos definir una función que implemente nuestra función.
En este caso, usaremos una versión de compensación simple de la función x ^ 2, p. Ej. una función de parábola simple (forma de U). Es una función objetivo de minimización con un óptimo en -5.0.
|
# función objetiva def objetivo(X): regreso (5,0 + X)**2.0 |
Podemos trazar una cuadrícula aproximada de esta función con valores de entrada de -10 a 10 para tener una idea de la forma de la función objetivo.
El ejemplo completo se enumera a continuación.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 dieciséis 17 |
# trazar una función objetivo convexa desde numpy importar arange desde matplotlib importar pyplot # función objetiva def objetivo(X): regreso (5,0 + X)**2.0 # definir rango r_min, r_max = –10.0, 10.0 # preparar insumos entradas = arange(r_min, r_max, 0,1) # calcular objetivos objetivos = [[objetivo(X) para X en entradas] # trazar entradas vs objetivo pyplot.trama(entradas, objetivos, ‘-‘) pyplot.show() |
La ejecución del ejemplo evalúa los valores de entrada en nuestro rango especificado usando nuestra función objetivo y crea un gráfico de las entradas de la función a las salidas de la función.
Podemos ver la forma de U de la función y que el objetivo está en -5.0.
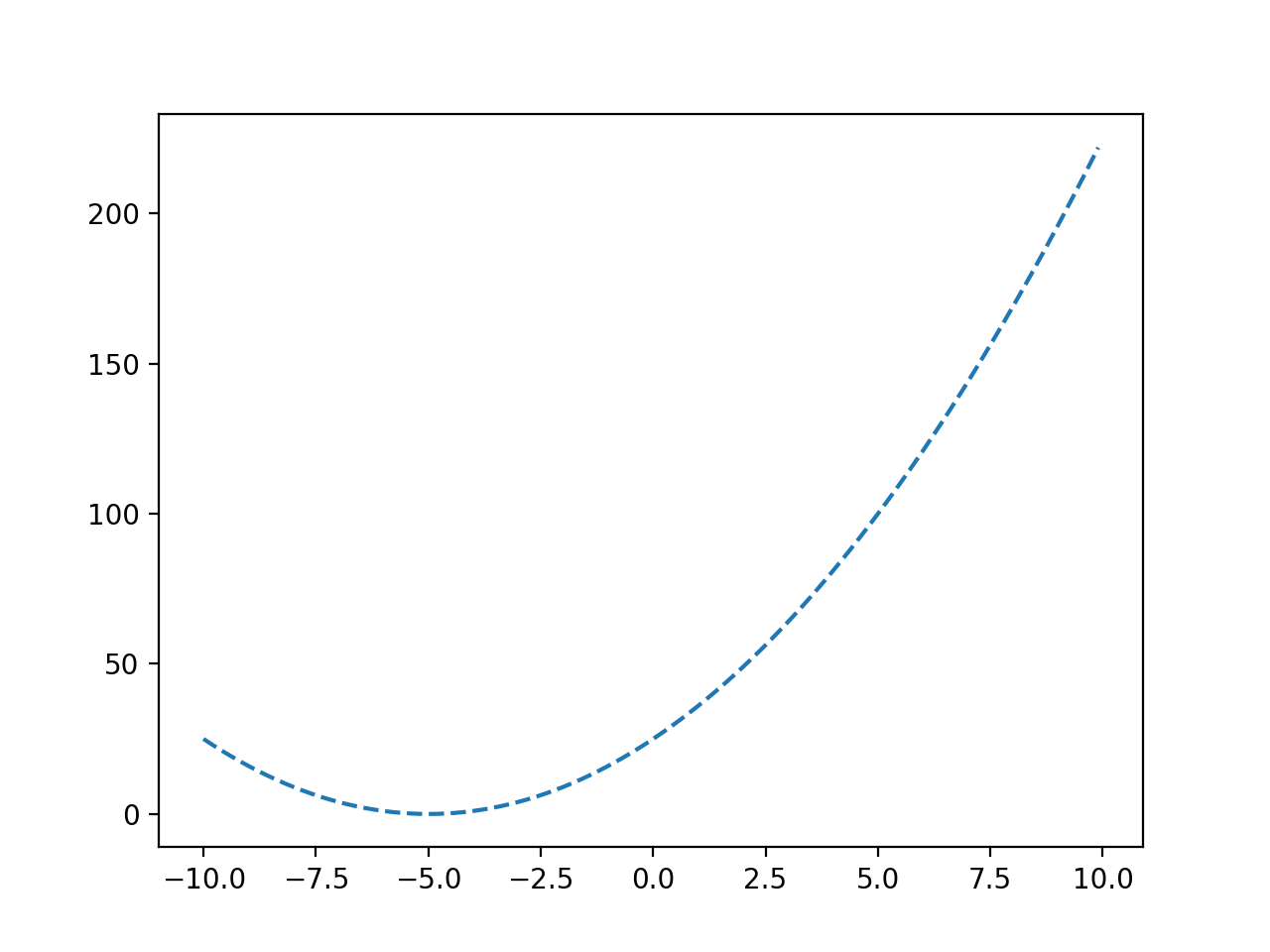
Gráfico de línea de una función objetiva convexa
Nota: en un problema de optimización real, no podríamos realizar tantas evaluaciones de la función objetivo con tanta facilidad. Esta sencilla función se utiliza con fines de demostración para que podamos aprender a utilizar el algoritmo de optimización.
A continuación, podemos utilizar el algoritmo de optimización para encontrar el óptimo.
|
... # minimizar la función resultado = minimizar_escalar(objetivo, método=‘brent’) |
Una vez optimizado, podemos resumir el resultado, incluyendo la entrada y evaluación de los óptimos y el número de evaluaciones de funciones necesarias para localizar los óptimos.
|
... # resumir el resultado opt_x, opt_y = resultado[[‘X’], resultado[[‘divertido’] impresión(‘Entrada óptima x:% .6f’ % opt_x) impresión(‘Salida óptima f (x):% .6f’ % opt_y) impresión(‘Evaluaciones totales n:% d’ % resultado[[‘nfev’]) |
Finalmente, podemos trazar la función nuevamente y marcar los óptimos para confirmar que estaba ubicada en el lugar que esperábamos para esta función.
|
... # definir el rango r_min, r_max = –10.0, 10.0 # preparar insumos entradas = arange(r_min, r_max, 0,1) # calcular objetivos objetivos = [[objetivo(X) para X en entradas] # trazar entradas vs objetivo pyplot.trama(entradas, objetivos, ‘-‘) # trazar el optima pyplot.trama([[opt_x], [[opt_y], ‘s’, color=‘r’) # mostrar la trama pyplot.show() |
El ejemplo completo de optimización de una función univariante convexa no restringida se muestra a continuación.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 dieciséis 17 18 19 20 21 22 23 24 25 26 27 28 |
# optimizar la función objetivo convexa desde numpy importar arange desde scipy.optimizar importar minimizar_escalar desde matplotlib importar pyplot # función objetiva def objetivo(X): regreso (5,0 + X)**2.0 # minimizar la función resultado = minimizar_escalar(objetivo, método=‘brent’) # resumir el resultado opt_x, opt_y = resultado[[‘X’], resultado[[‘divertido’] impresión(‘Entrada óptima x:% .6f’ % opt_x) impresión(‘Salida óptima f (x):% .6f’ % opt_y) impresión(‘Evaluaciones totales n:% d’ % resultado[[‘nfev’]) # definir el rango r_min, r_max = –10.0, 10.0 # preparar insumos entradas = arange(r_min, r_max, 0,1) # calcular objetivos objetivos = [[objetivo(X) para X en entradas] # trazar entradas vs objetivo pyplot.trama(entradas, objetivos, ‘-‘) # trazar el optima pyplot.trama([[opt_x], [[opt_y], ‘s’, color=‘r’) # mostrar la trama pyplot.show() |
Ejecutar el ejemplo primero resuelve el problema de optimización e informa el resultado.
Nota: Sus resultados pueden variar dada la naturaleza estocástica del algoritmo o procedimiento de evaluación, o las diferencias en la precisión numérica. Considere ejecutar el ejemplo varias veces y compare el resultado promedio.
En este caso, podemos ver que el óptimo se ubicó luego de 10 evaluaciones de la función objetivo con una entrada de -5.0, logrando un valor de función objetivo de 0.0.
|
Entrada óptima x: -5,000000 Salida óptima f (x): 0.000000 Total de evaluaciones n: 10 |
Se vuelve a crear un gráfico de la función y, esta vez, el óptimo se marca como un cuadrado rojo.
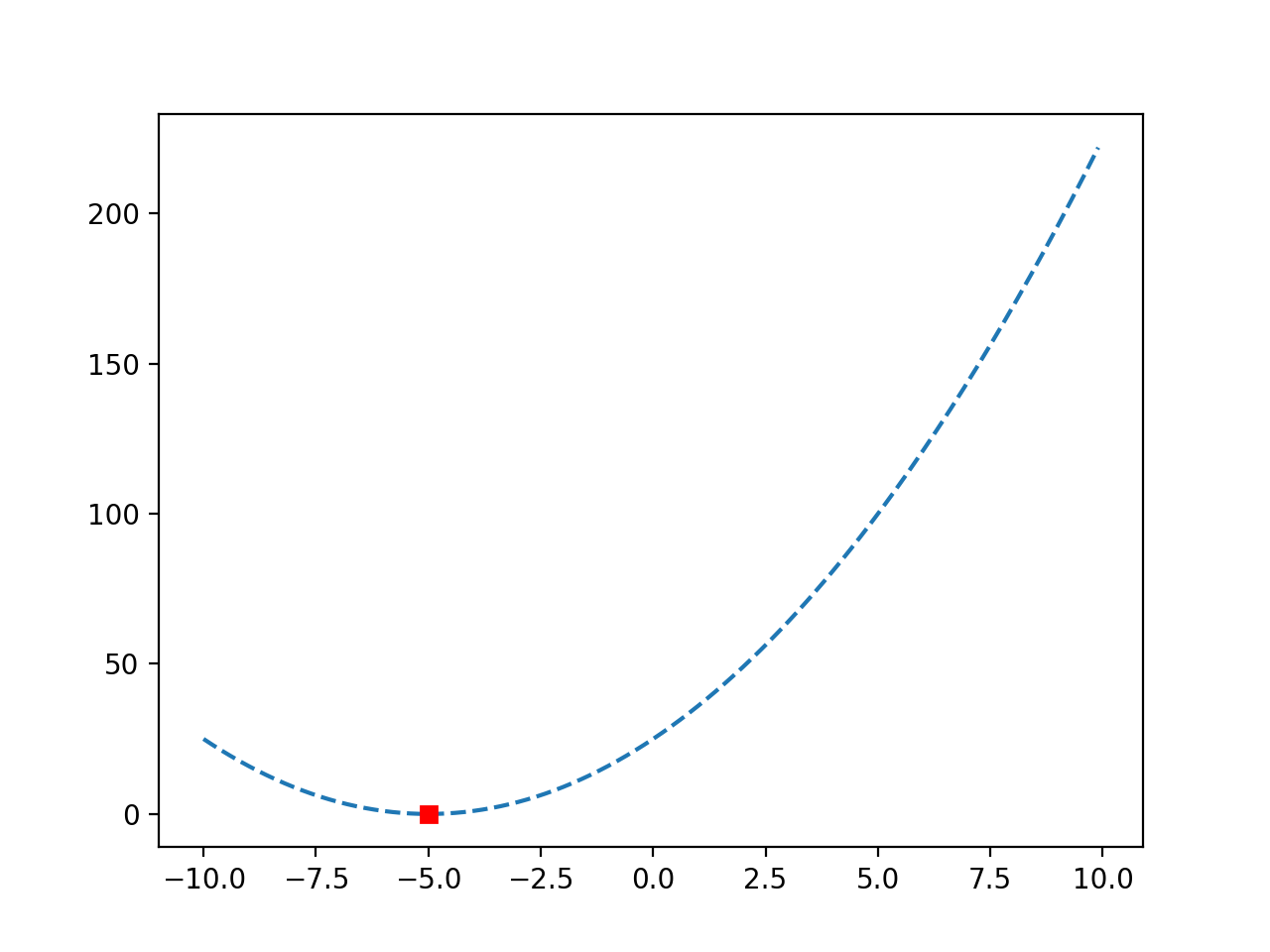
Gráfico de línea de una función objetiva convexa con Optima marcado
Optimización de funciones univariadas no convexas
Una función convexa es aquella que no se parece a una cuenca, lo que significa que puede tener más de una colina o valle.
Esto puede hacer que sea más difícil localizar los óptimos globales, ya que las múltiples colinas y valles pueden hacer que la búsqueda se atasque y, en su lugar, informe de un óptimo local o falso.
Podemos definir una función univariante no convexa de la siguiente manera.
|
# función objetiva def objetivo(X): regreso (X – 2.0) * X * (X + 2.0)**2.0 |
Podemos muestrear esta función y crear una gráfica lineal de valores de entrada a valores objetivos.
El ejemplo completo se enumera a continuación.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 dieciséis 17 |
# trazar una función univariante no convexa desde numpy importar arange desde matplotlib importar pyplot # función objetiva def objetivo(X): regreso (X – 2.0) * X * (X + 2.0)**2.0 # definir rango r_min, r_max = –3,0, 2.5 # preparar insumos entradas = arange(r_min, r_max, 0,1) # calcular objetivos objetivos = [[objetivo(X) para X en entradas] # trazar entradas vs objetivo pyplot.trama(entradas, objetivos, ‘-‘) pyplot.show() |
La ejecución del ejemplo evalúa los valores de entrada en nuestro rango especificado usando nuestra función objetivo y crea un gráfico de las entradas de la función a las salidas de la función.
Podemos ver una función con un falso óptimo alrededor de -2.0 y un óptimo global alrededor de 1.2.
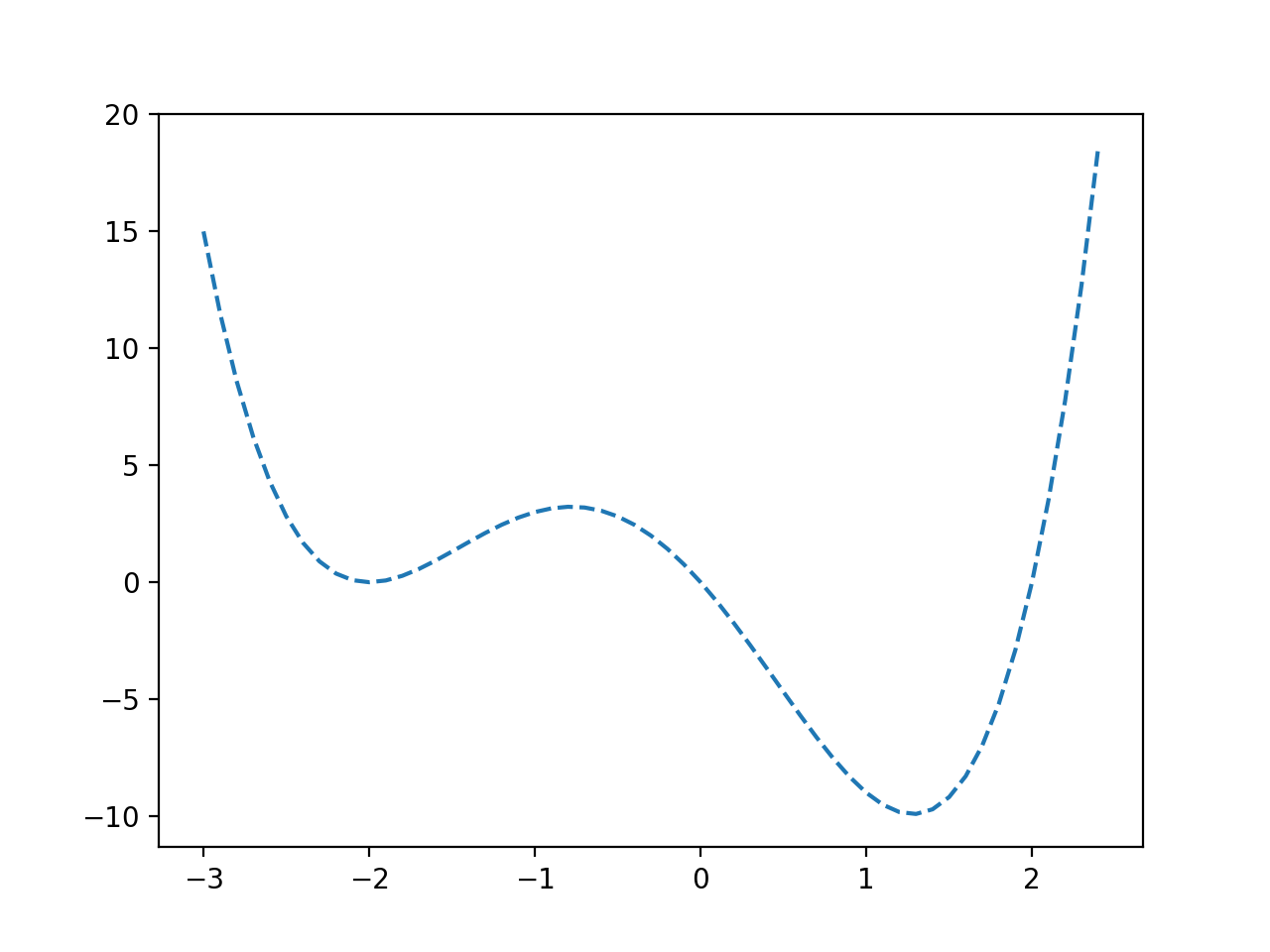
Gráfico de línea de una función objetivo no convexa
Nota: en un problema de optimización real, no podríamos realizar tantas evaluaciones de la función objetivo con tanta facilidad. Esta sencilla función se utiliza con fines de demostración para que podamos aprender a utilizar el algoritmo de optimización.
A continuación, podemos utilizar el algoritmo de optimización para encontrar el óptimo.
Como antes, podemos llamar a la función minim_scalar () para optimizar la función, luego resumir el resultado y graficar los óptimos en una gráfica lineal.
El ejemplo completo de optimización de una función univariante no convexa sin restricciones se enumera a continuación.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 dieciséis 17 18 19 20 21 22 23 24 25 26 27 28 |
# optimizar la función objetivo no convexa desde numpy importar arange desde scipy.optimizar importar minimizar_escalar desde matplotlib importar pyplot # función objetiva def objetivo(X): regreso (X – 2.0) * X * (X + 2.0)**2.0 # minimizar la función resultado = minimizar_escalar(objetivo, método=‘brent’) # resumir el resultado opt_x, opt_y = resultado[[‘X’], resultado[[‘divertido’] impresión(‘Entrada óptima x:% .6f’ % opt_x) impresión(‘Salida óptima f (x):% .6f’ % opt_y) impresión(‘Evaluaciones totales n:% d’ % resultado[[‘nfev’]) # definir el rango r_min, r_max = –3,0, 2.5 # preparar insumos entradas = arange(r_min, r_max, 0,1) # calcular objetivos objetivos = [[objetivo(X) para X en entradas] # trazar entradas vs objetivo pyplot.trama(entradas, objetivos, ‘-‘) # trazar el optima pyplot.trama([[opt_x], [[opt_y], ‘s’, color=‘r’) # mostrar la trama pyplot.show() |
Ejecutar el ejemplo primero resuelve el problema de optimización e informa el resultado.
¿Quiere empezar con Ensemble Learning?
Realice ahora mi curso intensivo de correo electrónico gratuito de 7 días (con código de muestra).
Haga clic para registrarse y obtener también una versión gratuita en formato PDF del curso.
Descarga tu minicurso GRATIS
En este caso, podemos ver que el óptimo se ubicó luego de 15 evaluaciones de la función objetivo con una entrada de alrededor de 1,28, logrando un valor de función objetivo de alrededor de -9,91.
|
Entrada óptima x: 1.280776 Salida óptima f (x): -9,914950 Total de evaluaciones n: 15 |
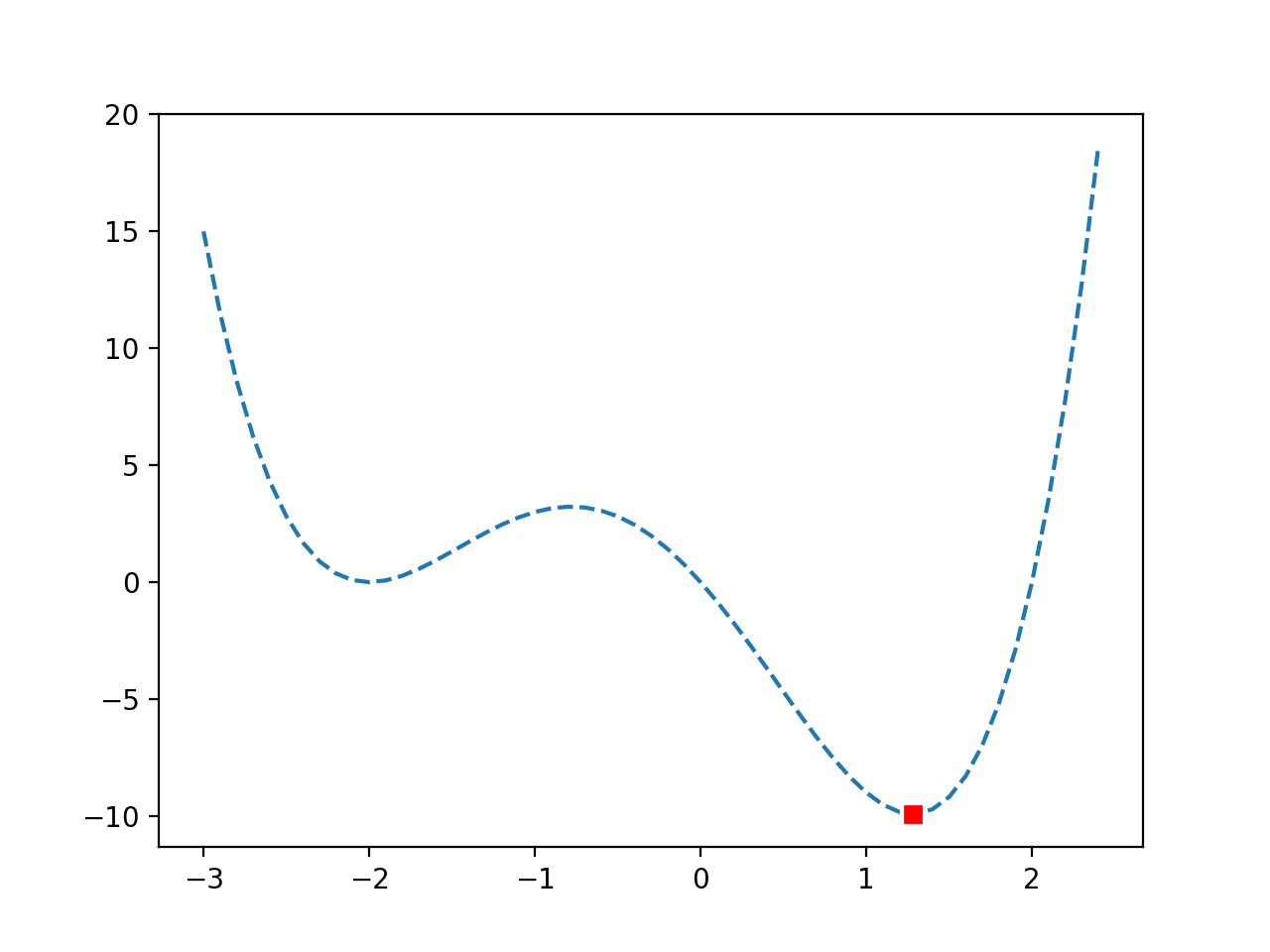
Se vuelve a crear un gráfico de la función y, esta vez, el óptimo se marca como un cuadrado rojo.
Podemos ver que la optimización no fue engañada por los falsos óptimos y ubicó exitosamente los óptimos globales.

Gráfico de línea de una función objetivo no convexa con Optima marcado
Otras lecturas
Esta sección proporciona más recursos sobre el tema si está buscando profundizar.
Libros
API
Artículos
Resumen
En este tutorial, descubrió cómo realizar la optimización de funciones univariadas en Python.
Específicamente, aprendiste:
- La optimización de funciones univariadas implica encontrar una entrada óptima para una función objetivo que toma un solo argumento continuo.
- Cómo realizar la optimización de una función univariante para una función convexa sin restricciones.
- Cómo realizar la optimización de una función univariante para una función no convexa sin restricciones.
¿Tiene usted alguna pregunta?
Haga sus preguntas en los comentarios a continuación y haré todo lo posible para responder.
