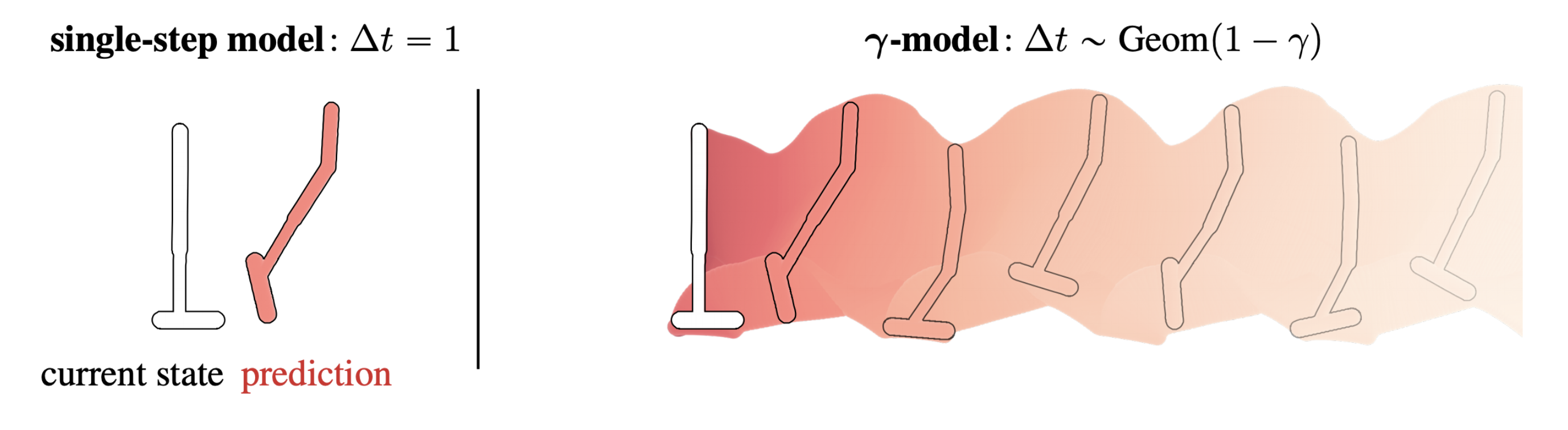
Los modelos estándar de un solo paso tienen un horizonte de uno. Esta publicación describe un método para entrenar modelos de dinámica predictiva en espacios de estados continuos con un horizonte probabilístico infinito.
Los algoritmos de aprendizaje por refuerzo se clasifican con frecuencia en función de si predicen estados futuros en cualquier punto de su proceso de toma de decisiones. Los que lo hacen se llaman basado en modelo, y los que no se apodan sin modelo. Esta clasificación es tan común que la mayoría de las veces la damos por sentada en estos días; Soy culpable de usarlo yo mismo. Sin embargo, esta distinción no es tan clara como parece inicialmente.
En esta publicación, hablaré sobre una visión alternativa que enfatiza el mecanismo de predicción en lugar del contenido de la predicción. Este cambio de enfoque pone de relieve un espacio entre los métodos basados en modelos y sin modelos que contiene direcciones interesantes para el aprendizaje por refuerzo. La primera mitad de esta publicación describe algunas de las herramientas clásicas en este espacio, incluyendo
funciones de valor generalizadas y la representación sucesora. La segunda mitad se basa en nuestro artículo reciente sobre modelos predictivos de horizonte infinito, cuyo código está disponible aquí.
los qué versus cómo de predicción
La dicotomía entre algoritmos basados en modelos y sin modelos se centra en lo que se predice directamente: estados o valores. En cambio, quiero centrarme en cómo se hacen estas predicciones y, específicamente, en cómo estos enfoques abordan las complejidades que surgen de los horizontes largos.
Los modelos dinámicos, por ejemplo, se aproximan a una distribución de transición de un solo paso, lo que significa que están entrenados en un problema de predicción con un horizonte de uno. Para que un modelo de horizonte corto sea útil para consultas de horizonte largo, sus predicciones de un solo paso se componen en forma de implementaciones secuenciales basadas en modelos. Podríamos decir que el horizonte de «prueba» de un método basado en modelos es el del despliegue.
Por el contrario, las funciones de valor en sí mismas son predictores a largo plazo; no es necesario que se utilicen en el contexto de los lanzamientos porque ya contienen información sobre el futuro ampliado. Para amortizar esta predicción a largo plazo, las funciones de valor se entrenan con estimaciones de Monte Carlo de la recompensa acumulada esperada o con programación dinámica. La distinción importante es ahora que la naturaleza a largo plazo de la tarea de predicción se aborda durante el entrenamiento en lugar de durante las pruebas.

Podemos organizar los algoritmos de aprendizaje por refuerzo en términos de cuándo se ocupan de la complejidad a largo plazo. Los modelos de dinámica se entrenan para una tarea de predicción de horizonte corto, pero se implementan mediante implementaciones de horizonte largo. En contraste, las funciones de valor amortizan el trabajo de predicción de horizonte largo en el entrenamiento, por lo que una predicción de un solo paso (e informalmente, un «horizonte» más corto) es suficiente durante la prueba.
Desde este punto de vista, el hecho de que los modelos predicen estados y las funciones de valor predicen recompensas acumulativas es casi un detalle. Lo que realmente importa es que los modelos predicen inmediato próximos estados y funciones de valor predicen sumas a largo plazo de recompensas. Esta idea está muy bien resumida en una línea de trabajo sobre funciones de valor generalizadas, que describe cómo se puede usar el aprendizaje de diferencias temporales para hacer predicciones a largo plazo sobre cualquier tipo de acumulativo, de las cuales una función de recompensa es simplemente un ejemplo.
Este encuadre también sugiere que algunos fenómenos que actualmente consideramos distintos, como los errores de predicción del modelo compuesto y la acumulación de errores de arranque, podrían ser en realidad lentes diferentes sobre el mismo problema. El primero describe el crecimiento del error en el transcurso de una implementación basada en modelos, y el segundo describe la propagación del error a través de la copia de seguridad de Bellman en el aprendizaje por refuerzo sin modelo. Si los modelos y las funciones de valor difieren principalmente en el momento en que se enfrentan a dificultades basadas en el horizonte, no debería sorprendernos que la combinación del error en el tiempo de prueba de los modelos tenga un análogo directo del tiempo de entrenamiento en las funciones de valor.
Una última razón para estar interesados en esta categorización alternativa es que nos permite pensar en híbridos que no tienen sentido bajo la dicotomía estándar. Por ejemplo, si un modelo hiciera predicciones de estado a largo plazo en virtud de la amortización del tiempo de entrenamiento, evitaría la necesidad de implementaciones secuenciales basadas en modelos y evitaría los errores de capitalización del tiempo de prueba. Las secciones restantes describen cómo podemos construir tal modelo, comenzando con la base de la representación sucesora y luego introduciendo un nuevo trabajo para hacer que esta forma de predicción sea compatible con espacios continuos y muestreadores neuronales.
La representación sucesora
La representación sucesora (SR), una idea influyente tanto en la ciencia cognitiva como en el aprendizaje automático, es un modelo de dinámica dependiente de políticas de largo horizonte. Aprovecha la idea de que el mismo tipo de relación de recurrencia utilizado para entrenar (Q ) – funciones:
[
Q(mathbf{s}_t, mathbf{a}_t) leftarrow
mathbb{E}_{mathbf{s}_{t+1}}
[r(mathbf{s}_{t}, mathbf{a}_t, mathbf{s}_{t+1}) + gamma V(mathbf{s}_{t+1})]
]también se puede usar para entrenar un modelo que predice estados en lugar de valores:
[
M(mathbf{s}_{t}, mathbf{a}_t) leftarrow
mathbb{E}_{mathbf{s}_{t+1}}
[mathbf{1}(mathbf{s}_{t+1}) + gamma M(mathbf{s}_{t+1})] etiqueta * {(1)}
]
La diferencia clave entre los dos es que el escalar recompensa (r ( mathbf {s} _t, mathbf {a} _t, mathbf {s} _ {t + 1}) ) del (Q ) -La recurrencia de funciones ahora se reemplaza con vectores indicadores de un solo uso ( mathbf {1} ( mathbf {s} _ {t + 1}) ) que denotan estados. Como tal, el entrenamiento de RS puede considerarse como aprendizaje (Q ) con valores vectoriales. El tamaño del vector de «recompensa», así como las predicciones sucesoras (M ( mathbf {s} _t, mathbf {a} _t) ) y (M ( mathbf {s} _t) ), es igual al número de estados del MDP.
A diferencia de los modelos de dinámica estándar, que se aproximan a una distribución de transición de un solo paso, SR se aproxima a lo que se conoce como ocupación con descuento:
[
mu(mathbf{s}_e mid mathbf{s}_t, mathbf{s}_t) = (1 – gamma)
sum_{Delta t=1}^{infty} gamma^{Delta t – 1}
p(
mathbf{s}_{t+Delta t} = mathbf{s}_e mid
mathbf{s}_t, mathbf{a}_t, pi
)
]
Esta ocupación es una mezcla ponderada sobre una serie infinita de modelos de varios pasos, con los pesos de la mezcla controlados por un factor de descuento ( gamma ). El establecimiento de ( gamma = 0 ) recupera un modelo estándar de un solo paso, y cualquier ( gamma in (0,1) ) induce un modelo con un horizonte probabilístico infinito. La anticipación predictiva del modelo aumenta cualitativamente con ( gamma ) más grande.
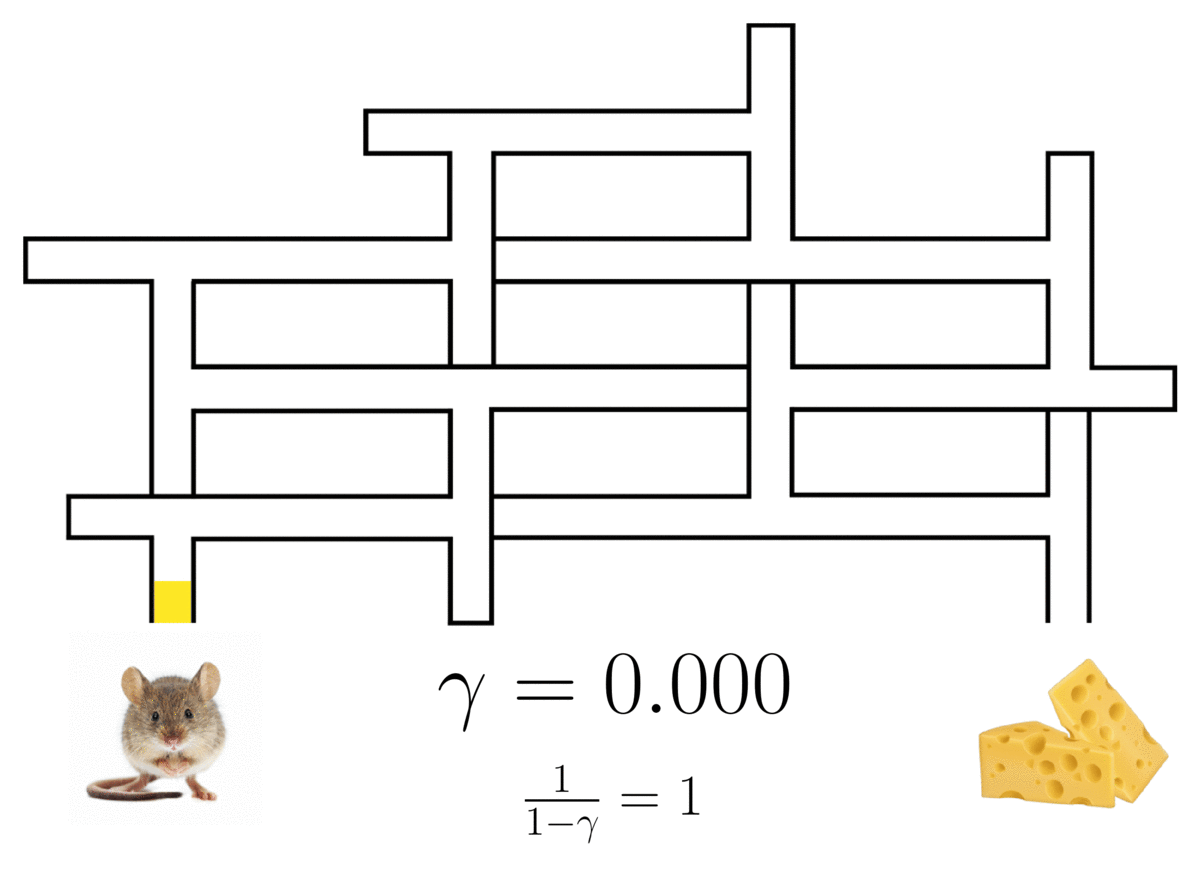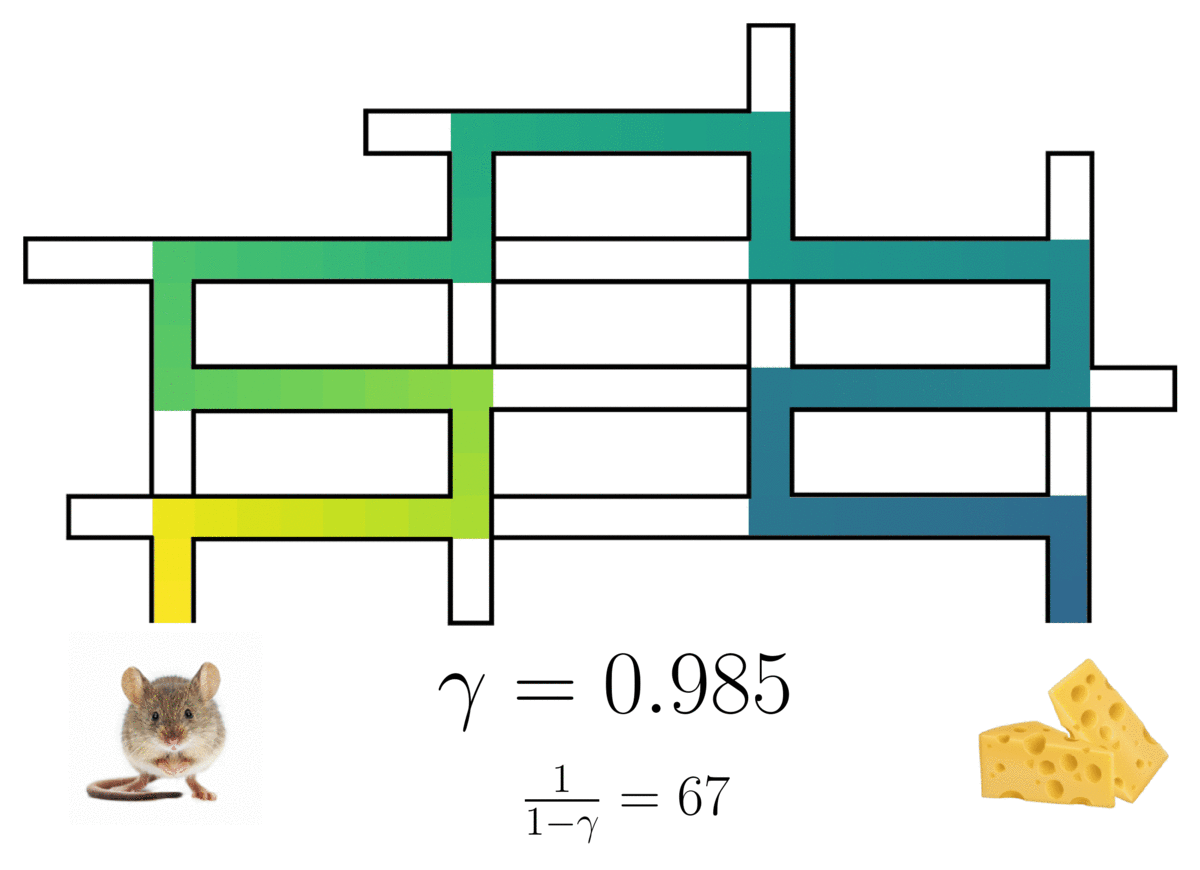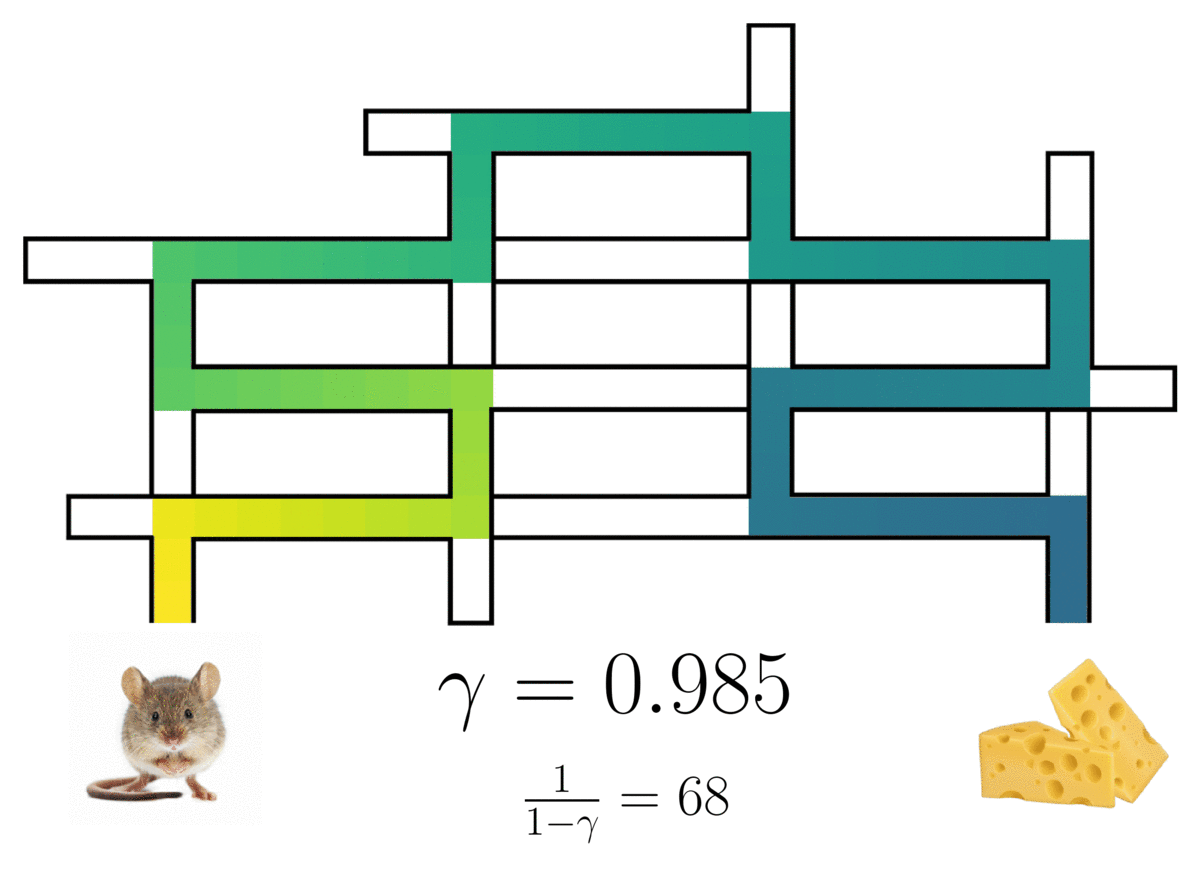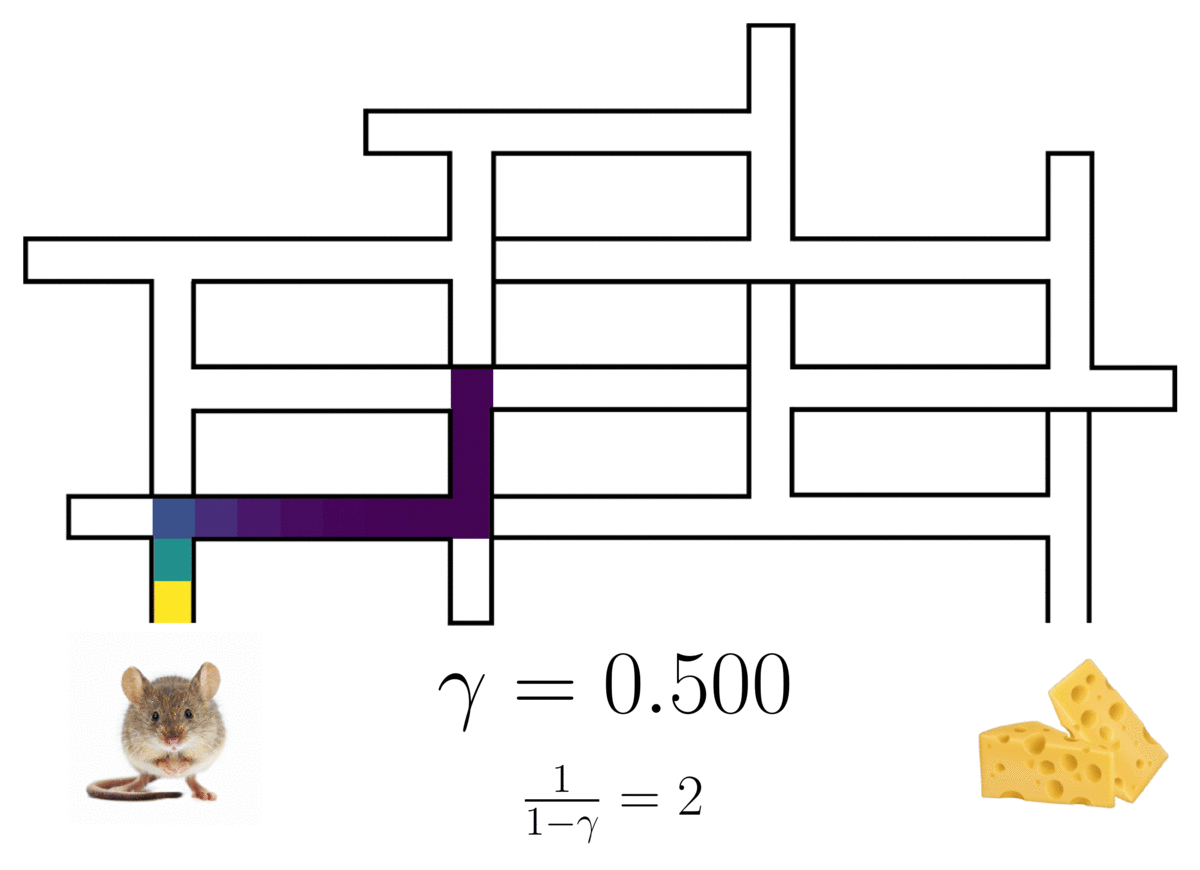
La representación sucesora de una rata (n óptima) en un laberinto, mostrando el camino de la rata con un horizonte probabilístico determinado por el factor de descuento ( gamma ).
Modelos generativos en espacios continuos: desde SR hasta ( boldsymbol { gamma} ) – modelos
Las adaptaciones continuas de SR reemplazan el indicador de estado único ( mathbf {1} ( mathbf {s} _t) ) en la Ecuación 1 con una característica de estado aprendido ( phi ( mathbf {s} _t, mathbf {a} _t) ), dando una recurrencia de la forma:
[
psi(mathbf{s}_t, mathbf{a}_t) leftarrow phi(mathbf{s}_t, mathbf{a}_t) + gamma
mathbb{E}_{mathbf{s}_{t+1}} [psi(mathbf{s}_{t+1})]
]
Este no es un modelo generativo en el sentido habitual, sino que se conoce como modelo de expectativa: ( psi ) denota el vector de características esperadas ( phi ). La ventaja de este enfoque es que un modelo de expectativas es más fácil de entrenar que un modelo generativo. Además, si las recompensas son lineales en las características, un modelo de expectativas es suficiente para la estimación del valor.
Sin embargo, la limitación de un modelo de expectativas es que no se puede emplear en algunos de los casos de uso más comunes de modelos de dinámica predictiva. Debido a que ( psi ( mathbf {s} _t, mathbf {a} _t) ) solo predice un primer momento, no podemos usarlo para muestrear estados futuros o realizar implementaciones basadas en modelos.
Para superar esta limitación, podemos convertir la actualización discriminativa utilizada en SR y sus variantes continuas en una adecuada para entrenar un modelo generativo ({ color {# D62728} mu} ):
[
max_{color{#D62728}mu} mathbb{E}_{mathbf{s}_t, mathbf{a}_t, mathbf{s}_{t+1} sim mathcal{D}} [ mathbb{E}_{
mathbf{s}_e sim (1-gamma) p(cdot mid mathbf{s}_t, mathbf{a}_t) + gamma
{color{#D62728}mu}(cdot mid mathbf{s}_{t+1})
}
[log {color{#D62728}mu}(mathbf{s}_e mid mathbf{s}_t, mathbf{a}_t)] ]]
A primera vista, esto parece un objetivo estándar de máxima probabilidad. La diferencia importante es que la distribución sobre la que se evalúa la expectativa interna depende del modelo ({ color {# D62728} mu} ) en sí. En lugar de un valor objetivo de arranque como los que se usan comúnmente en los algoritmos sin modelo, ahora tenemos una distribución de objetivo de arranque.
[
underset{
vphantom{HugeSigma}
Large text{target value}
}{
r + gamma V
}
~~~~~~~~ Longleftrightarrow ~~~~~~~~
underset{
vphantom{HugeSigma}
Large text{target }color{#D62728}{text{distribution}}
}{
(1-gamma) p + gamma {color{#D62728}mu}
}
]
Al variar el factor de descuento ( gamma ) en la distribución objetivo, se obtienen modelos que predicen cada vez más en el futuro.
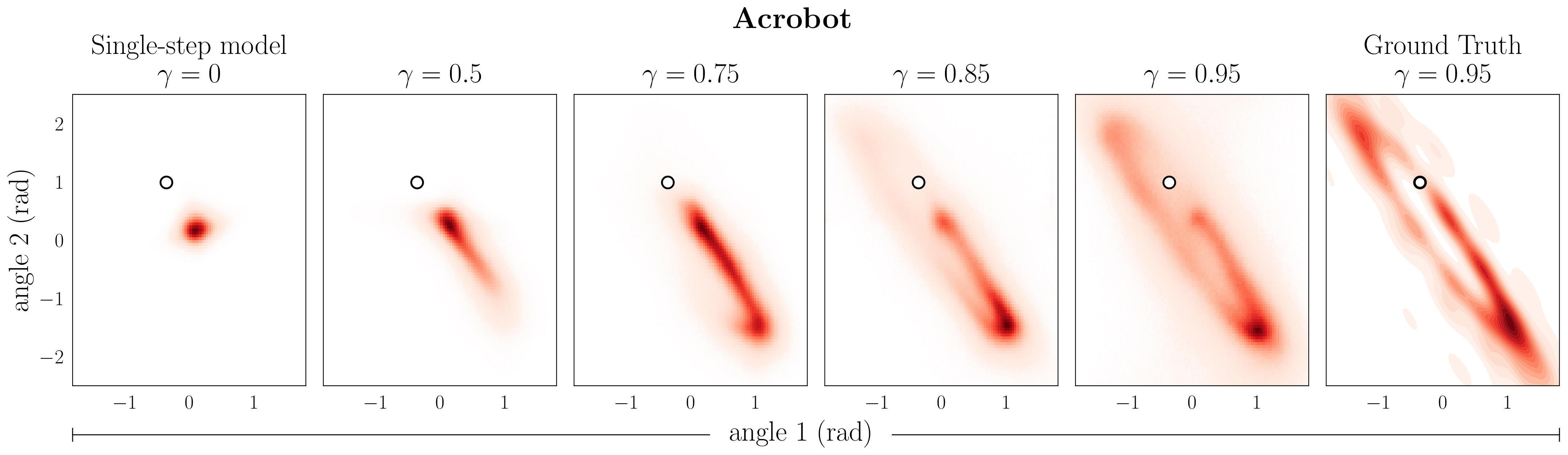
Predicciones de un modelo ( gamma ) – para descuentos variables ( gamma ). La columna de la derecha muestra las estimaciones de Monte Carlo de la ocupación con descuento correspondiente a ( gamma = 0,95 ) como referencia. El estado de condicionamiento se denota por ( circ ).
En el espíritu del control libre de modelos de horizonte infinito, nos referimos a esta formulación como predicción de horizonte infinito y al modelo correspondiente como modelo ( gamma ). Debido a que el objetivo de máxima verosimilitud de bootstrap evita la necesidad de vectores de recompensa del tamaño del espacio de estados, el entrenamiento del modelo ( gamma ) es adecuado para espacios continuos mientras se conserva una interpretación como modelo generativo. En nuestro artículo mostramos cómo instanciar ( gamma ) – modelos tanto como flujos normalizadores como redes generativas adversarias.
Generalización del control basado en modelos con ( boldsymbol { gamma} ) – modelos
Reemplazar los modelos de dinámica de un solo paso con ( gamma ) – modelos conduce a generalizaciones de algunos de los elementos básicos del control basado en modelos:
Implementaciones: ( gamma ): modela el paso de tiempo de divorcio del paso del modelo. A diferencia de incrementar un paso de tiempo en el futuro con cada predicción, ( gamma ) – los pasos de implementación del modelo tienen una distribución binomial negativa a lo largo del tiempo. Es posible volver a ponderar estos ( gamma ) – pasos del modelo para simular las predicciones de un modelo entrenado con un mayor descuento.
Mientras que los modelos de dinámica convencionales predicen un solo paso hacia el futuro, ( gamma ) – los pasos de implementación del modelo tienen una distribución binomial negativa a lo largo del tiempo. El primer paso de un modelo ( gamma ) – tiene una distribución geométrica del caso especial de (~ text {NegBinom} (1, p) = text {Geom} (1-p) ).
Estimación de valor: Los modelos de un solo paso estiman los valores utilizando implementaciones largas basadas en modelos, a menudo entre decenas y cientos de pasos. En contraste, los valores son expectativas sobre una sola pasada de retroalimentación de un modelo ( gamma ) -. Esto es similar a una descomposición del valor como producto interno, como se ve en las características sucesoras y la SR profunda. En los espacios tabulares con recompensas de indicadores, ¡el producto interno y la expectativa son los mismos!
Debido a que los valores son expectativas de recompensa en un solo paso de un modelo ( gamma ), podemos realizar una estimación de valor sin implementaciones secuenciales basadas en modelos.
Funciones de valor terminal: Para tener en cuenta el error de truncamiento en implementaciones basadas en modelos de un solo paso, es común aumentar la implementación con una función de valor terminal. Esta estrategia, a veces denominada expansión de valor basada en modelo (MVE), tiene un traspaso abrupto entre la implementación basada en modelo y la función de valor sin modelo. Podemos derivar una estrategia análoga con un modelo ( gamma ), llamado ( gamma ) – MVE, que presenta una transición gradual entre la estimación de valor basada en modelo y sin modelo. Esta estrategia de estimación de valor se puede incorporar en un algoritmo de aprendizaje por refuerzo basado en modelos para mejorar la eficiencia de la muestra.
( gamma ) – MVE presenta una transición gradual entre la estimación de valor basada en modelo y sin modelo.
Esta publicación se basa en el siguiente documento:
Referencias
- A Barreto, W Dabney, R Munos, JJ Hunt, T Schaul, HP van Hasselt y D Silver. Funciones sucesoras para la transferencia en el aprendizaje por refuerzo. NeurIPS 2017.
- P Dayan. Mejora de la generalización para el aprendizaje de diferencias temporales: la representación del sucesor. Computación neuronal 1993.
- Vladimir Feinberg, Alvin Wan, Ion Stoica, Michael I. Jordan, Joseph E. Gonzalez, Sergey Levine. Estimación de valor basada en modelos para un aprendizaje por refuerzo eficiente sin modelos. ICML 2018.
- SJ Gershman. La representación sucesora: Su lógica computacional y sustratos neuronales. Revista de neurociencia 2018.
- IJ Goodfellow, J Pouget-Abadie, M Mirza, B Xu, D Warde-Farley, S Ozair, A Courville, Y Bengio. Redes generativas antagónicas. NeurIPS 2014.
- M Janner, J Fu, M Zhang, S Levine. Cuándo confiar en su modelo: optimización de políticas basada en modelos. NeurIPS 2019.
- TD Kulkarni, A Saeedi, S Gautam y SJ Gershman. Aprendizaje profundo por refuerzo sucesor. 2016.
- A Kumar, J Fu, G Tucker, S Levine. Estabilización fuera de la política (Q ): aprendizaje mediante la reducción de errores de bootstrapping. NeurIPS 2019.
- HR Maei y RS Sutton. GQ ( ( lambda )): un algoritmo de gradiente general para el aprendizaje de la predicción de diferencias temporales con trazas de elegibilidad. AGI 2010.
- Yo Momennejad, EM Russek, JH Cheong, MM Botvinick, ND Daw y SJ Gershman. La representación sucesora en el aprendizaje por refuerzo humano. Comportamiento humano de la naturaleza 2017.
- DJ Rezende y S Mohamed. Inferencia variacional con normalización de flujos. ICML 2015.
- RS Sutton. Modelos TD: modelando el mundo en una mezcla de escalas de tiempo. ICML 1995.
- RS Sutton, J Modayil, M Delp, T Degris, PM Pilarski, A White y D Precup. Horde: una arquitectura escalable en tiempo real para aprender conocimientos a partir de la interacción sensoriomotora no supervisada. AAMAS 2011.
- RS Sutton, D Precup y S Singh. Entre MDP y semi-MDP: un marco para la abstracción temporal en el aprendizaje por refuerzo. Inteligencia artificial 1999.
- E Tolman. Mapas cognitivos en ratas y hombres. Revisión psicológica 1948.
- Un blanco. Desarrollar un enfoque predictivo del conocimiento. Tesis doctoral, 2015.
