Las redes neuronales profundas han permitido maravillas tecnológicas que van desde el reconocimiento de voz hasta la transición de máquinas a la ingeniería de proteínas, pero su diseño y aplicación, no obstante, carecen de principios. El desarrollo de herramientas y métodos para guiar este proceso es uno de los grandes desafíos de la teoría del aprendizaje profundo. En Reverse Engineering the Neural Tangent Kernel, proponemos un paradigma para llevar algún principio al arte del diseño de arquitectura utilizando avances teóricos recientes: primero diseñe una buena función de kernel, a menudo una tarea mucho más fácil, y luego «ingeniería inversa» una red. equivalencia del kernel para traducir el kernel elegido en una red neuronal. Nuestro principal resultado teórico permite el diseño de funciones de activación desde los primeros principios, y lo usamos para crear una función de activación que imita el rendimiento de la red profunda (textrm{ReLU}) con solo una capa oculta y otra que supera ampliamente el rendimiento de la ( textrm{ReLU}) redes en una tarea sintética.
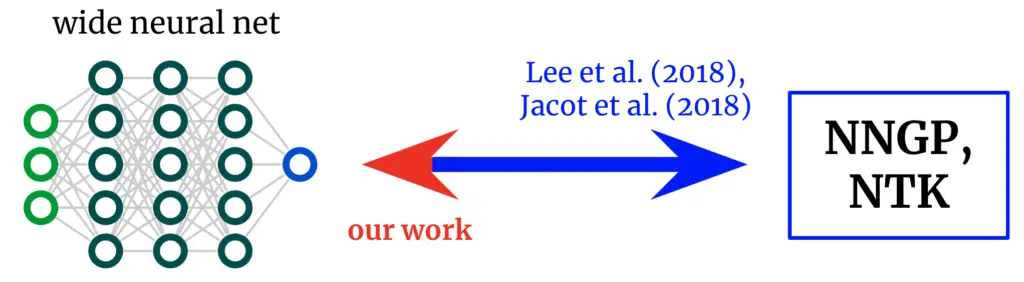
Kernels de vuelta a las redes. Los trabajos fundamentales derivaron fórmulas que mapean desde amplias redes neuronales hasta sus núcleos correspondientes. Obtenemos un mapeo inverso, que nos permite partir de un núcleo deseado y convertirlo nuevamente en una arquitectura de red.
Núcleos de redes neuronales
El campo de la teoría del aprendizaje profundo se ha transformado recientemente al darse cuenta de que las redes neuronales profundas a menudo se vuelven analíticamente tratables para estudiar en el ancho infinito límite. Tome el límite de cierta manera y, de hecho, la red converge a un método de núcleo normal utilizando el «núcleo tangente neuronal» (NTK) de la arquitectura o, si solo se entrena la última capa (al estilo de los modelos de características aleatorias), su «núcleo neuronal tangente». Núcleo del proceso gaussiano de red (NNGP). Al igual que el teorema del límite central, estos límites de red amplia a menudo son aproximaciones sorprendentemente buenas incluso lejos del ancho infinito (a menudo se cumplen en anchos de cientos o miles), lo que brinda un manejo analítico notable de los misterios del aprendizaje profundo.
De las redes a los núcleos y viceversa
Los trabajos originales que exploran esta correspondencia net-kernel dieron fórmulas para pasar de arquitectura a núcleo: dada una descripción de una arquitectura (por ejemplo, profundidad y función de activación), le brindan los dos núcleos de la red. Esto ha permitido grandes conocimientos sobre la optimización y generalización de varias arquitecturas de interés. Sin embargo, si nuestro objetivo no es meramente entender las arquitecturas existentes sino diseñar nuevo unos, entonces podríamos tener el mapeo en la dirección inversa: dada una núcleo queremos, podemos encontrar un arquitectura que nos da? En este trabajo, derivamos este mapeo inverso para redes totalmente conectadas (FCN), lo que nos permite diseñar redes simples de manera basada en principios al (a) postular un kernel deseado y (b) diseñar una función de activación que lo proporcione.
Para ver por qué esto tiene sentido, primero visualicemos un NTK. Considere un NTK de FCN ancho (K(x_1,x_2)) en dos vectores de entrada (x_1) y (x_2) (que, por simplicidad, supondremos que están normalizados a la misma longitud). Para un FCN, este núcleo es rotación-invariante en el sentido de que (K(x_1,x_2) = K(c)), donde (c) es el coseno del ángulo entre las entradas. Dado que (K(c)) es una función escalar de un argumento escalar, podemos simplemente trazarlo. La figura 2 muestra el NTK de un FCN de cuatro capas ocultas (4HL) (textrm{ReLU}).
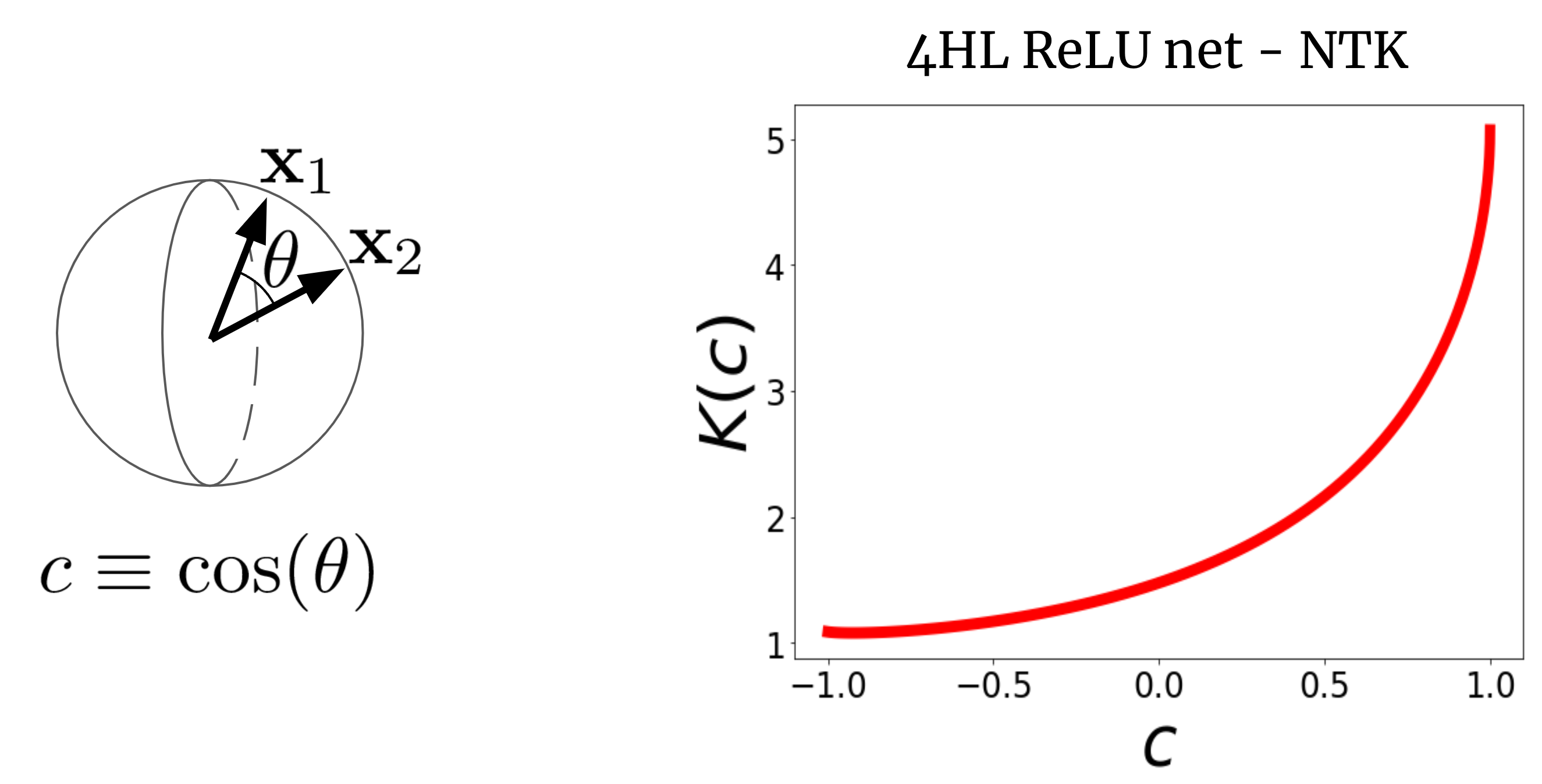
Figura 2. El NTK de un 4HL $textrm{ReLU}$ FCN en función del coseno entre dos vectores de entrada $x_1$ y $x_2$.
¡Esta gráfica en realidad contiene mucha información sobre el comportamiento de aprendizaje de la red amplia correspondiente! El aumento monótono significa que este kernel espera que los puntos más cercanos tengan valores de función más correlacionados. El fuerte aumento al final nos dice que la longitud de la correlación no es demasiado grande y que puede ajustarse a funciones complicadas. La derivada divergente en (c=1) nos informa sobre la suavidad de la función que esperamos obtener. En tono rimbombante, ninguno de estos hechos es evidente al observar un gráfico de (textrm{ReLU}(z))! Afirmamos que, si queremos comprender el efecto de elegir una función de activación (phi), entonces el NTK resultante es en realidad más informativo que (phi) en sí mismo. Por lo tanto, tal vez tenga sentido intentar diseñar arquitecturas en el «espacio del kernel» y luego traducirlas a los típicos hiperparámetros.
Una función de activación para cada núcleo
Nuestro resultado principal es un «teorema de ingeniería inversa» que establece lo siguiente:
Thm 1: Para cualquier kernel $K(c)$, podemos construir una función de activación $tilde{phi}$ tal que, cuando se inserta en un una sola capa oculta FCN, su kernel NTK o NNGP de ancho infinito es $K(c)$.
Damos una fórmula explícita para (tilde{phi}) en términos de polinomios de Hermite (aunque usamos una forma funcional diferente en la práctica por razones de entrenamiento). Nuestro uso propuesto de este resultado es que, en problemas con alguna estructura conocida, a veces será posible escribir un buen núcleo y aplicarle ingeniería inversa en una red entrenable con varias ventajas sobre la regresión pura del núcleo, como la eficiencia computacional y la capacidad de aprender características. Como prueba de concepto, probamos esta idea en el sintético problema de paridad (es decir, dada una cadena de bits, ¿la suma es par o impar?), generando inmediatamente una función de activación que supera dramáticamente a (text{ReLU}) en la tarea.
¿Una capa oculta es todo lo que necesitas?
Aquí hay otro uso sorprendente de nuestro resultado. La curva del kernel anterior es para un FCN 4HL (textrm{ReLU}), pero afirmé que podemos lograr cualquier kernel, incluido ese, con solo una capa oculta. Esto implica que podemos crear una nueva función de activación (tilde{phi}) que proporcione este NTK «profundo» en un red poco profunda! La Fig. 3 ilustra este experimento.
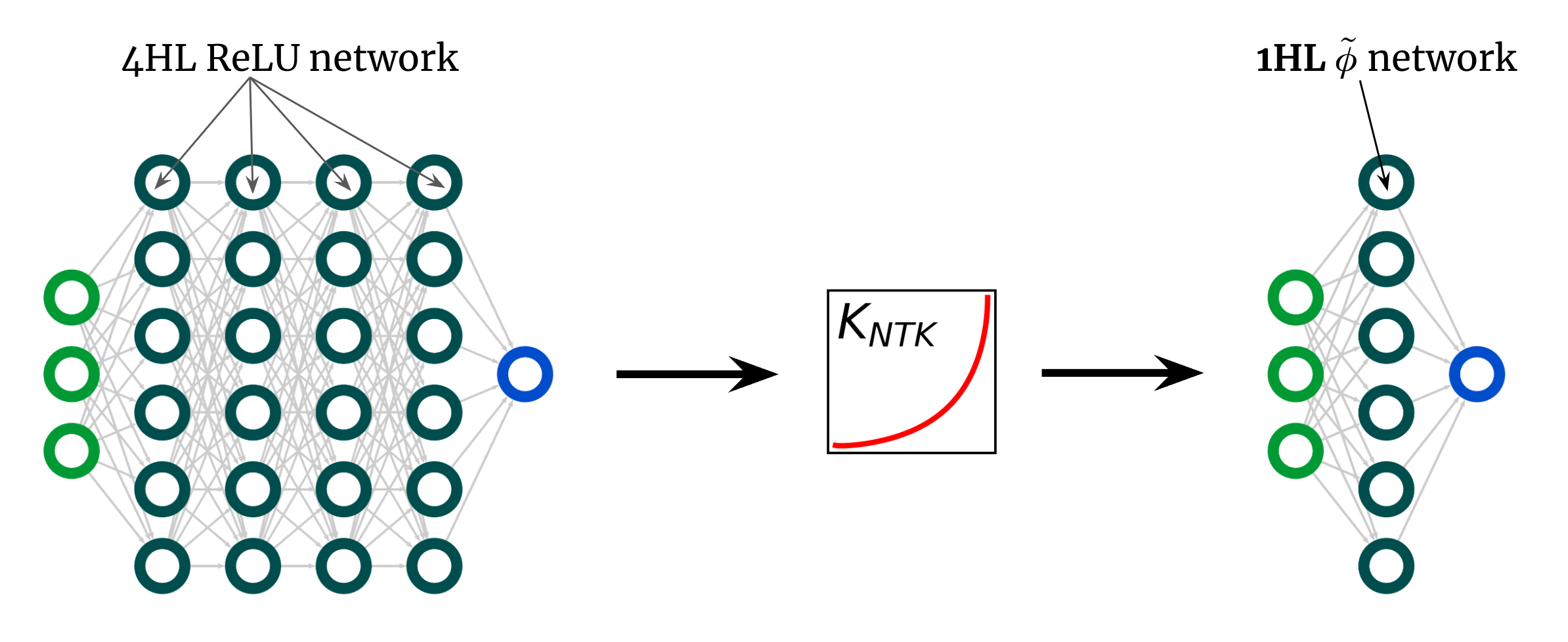
Fig. 3. Superficialización de un $textrm{ReLU}$ FCN profundo en un 1HL FCN con una función de activación diseñada $tilde{phi}$.
Sorprendentemente, esta «superficialización» realmente funciona. La subparcela izquierda de la Fig. 4 a continuación muestra una función de activación «mímica» (tilde{phi}) que proporciona prácticamente el mismo NTK que un (textrm{ReLU}) FCN profundo. Las gráficas de la derecha muestran el tren + pérdida de prueba + trazas de precisión para tres FCN en un problema tabular estándar del conjunto de datos de UCI. Tenga en cuenta que, si bien las redes ReLU superficiales y profundas tienen comportamientos muy diferentes, ¡nuestra red mímica superficial diseñada rastrea la red profunda casi exactamente!
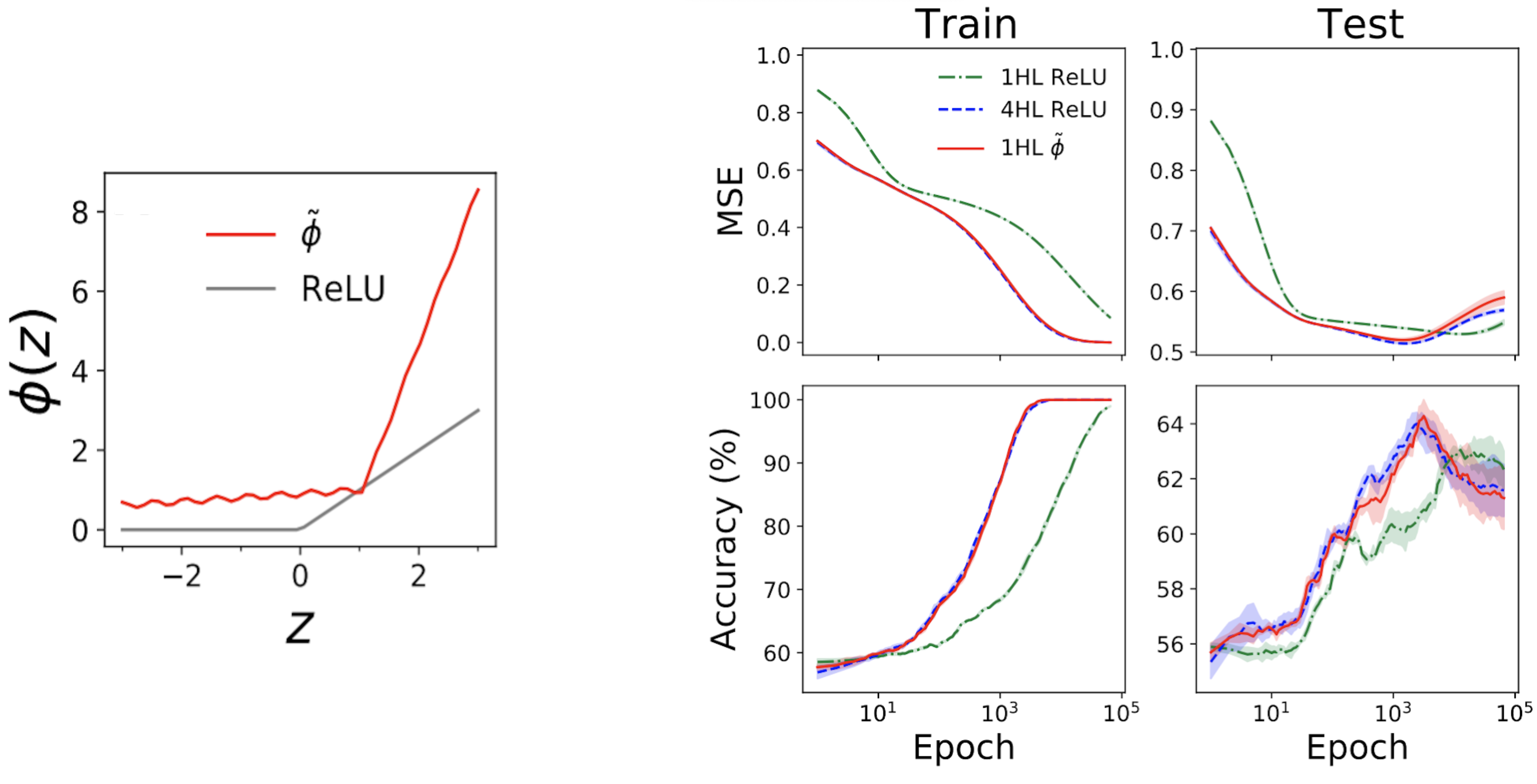
Figura 4. Panel izquierdo: nuestra función de activación «imitadora» diseñada, trazada con ReLU para comparar. Paneles de la derecha: seguimientos de rendimiento para 1HL ReLU, 4HL ReLU y 1HL imitan FCN entrenados en un conjunto de datos de UCI. Tenga en cuenta la estrecha coincidencia entre las redes mímicas 4HL ReLU y 1HL.
Esto es interesante desde una perspectiva de ingeniería porque la red superficial utiliza menos parámetros que la red profunda para lograr el mismo rendimiento. También es interesante desde una perspectiva teórica porque plantea preguntas fundamentales sobre el valor de la profundidad. Una creencia común en el aprendizaje profundo es que más profundo no solo es mejor sino cualitativamente diferente: que las redes profundas aprenderán eficientemente funciones que las redes superficiales simplemente no pueden. Nuestro resultado de superficialización sugiere que, al menos para las FCN, esto no es cierto: si sabemos lo que estamos haciendo, entonces la profundidad no nos compra nada.
Conclusión
Este trabajo viene con muchas advertencias. El mayor es que nuestro resultado solo se aplica a los FCN, que por sí solos rara vez son de última generación. Sin embargo, el trabajo en NTK convolucionales está progresando rápidamente, y creemos que este paradigma de diseño de redes mediante el diseño de núcleos está listo para extenderse de alguna forma a estas arquitecturas estructuradas.
Hasta ahora, el trabajo teórico ha proporcionado relativamente pocas herramientas para los teóricos prácticos del aprendizaje profundo. Nuestro objetivo es que este sea un paso modesto en esa dirección. Incluso sin una ciencia que guíe su diseño, las redes neuronales ya han permitido maravillas. Imagínese lo que podremos hacer con ellos una vez que finalmente tengamos uno.
Esta publicación se basa en el documento «Reverse Engineering the Neural Tangent Kernel», que es un trabajo conjunto con Sajant Anand y Mike DeWeese. Proporcionamos código para reproducir todos nuestros resultados. Estaremos encantados de responder a sus preguntas o comentarios.
