Autoencoder es un tipo de red neuronal que puede utilizarse para aprender una representación comprimida de los datos en bruto.
Un autoencoder está compuesto por un codificador y un decodificador sub-modelos. El codificador comprime la entrada y el decodificador intenta recrear la entrada a partir de la versión comprimida proporcionada por el codificador. Después de la formación, el modelo de codificador se guarda y el decodificador se descarta.
El codificador puede utilizarse entonces como técnica de preparación de datos para realizar la extracción de características en los datos en bruto que pueden utilizarse para entrenar un modelo diferente de aprendizaje de la máquina.
En este tutorial, descubrirá cómo desarrollar y evaluar un autoencoder para el modelado predictivo de clasificación.
Después de completar este tutorial, lo sabrás:
- Un autoencoder es un modelo de red neural que puede ser usado para aprender una representación comprimida de los datos en bruto.
- Cómo entrenar un modelo de autoencoder en un conjunto de datos de entrenamiento y guardar sólo la parte de codificador del modelo.
- Cómo usar el codificador como un paso de preparación de datos cuando se entrena un modelo de aprendizaje de una máquina.
Empecemos.

Cómo desarrollar un autoencoder para la clasificación
Foto de Bernd Thaller, algunos derechos reservados.
Resumen del Tutorial
Este tutorial está dividido en tres partes; son:
- Autocodificadores para la extracción de características
- Autoencoder para la clasificación
- El codificador como preparación de datos para el modelo de predicción
Autocodificadores para la extracción de características
Un autoencoder es un modelo de red neural que busca aprender una representación comprimida de una entrada.
Un autoencoder es una red neural que está entrenada para intentar copiar su entrada a su salida.
– Página 502, Aprendizaje profundo, 2016.
Se trata de un método de aprendizaje no supervisado, aunque técnicamente se les entrena utilizando métodos de aprendizaje supervisados, denominados auto-supervisados.
Los autocodificadores suelen ser entrenados como parte de un modelo más amplio que intenta recrear la entrada.
Por ejemplo:
El diseño del modelo de autoencoder lo hace difícil a propósito, restringiendo la arquitectura a un cuello de botella en el punto medio del modelo, a partir del cual se realiza la reconstrucción de los datos de entrada.
Hay muchos tipos de autocodificadores y su uso varía, pero quizás el uso más común es como modelo de extracción de características aprendidas o automáticas.
En este caso, una vez que el modelo se ajusta, el aspecto de la reconstrucción del modelo puede ser descartado y el modelo hasta el punto del cuello de botella puede ser utilizado. La salida del modelo en el cuello de botella es un vector de longitud fija que proporciona una representación comprimida de los datos de entrada.
Por lo general, están restringidos de manera que sólo pueden copiar aproximadamente, y copiar sólo la entrada que se asemeja a los datos de entrenamiento. Dado que el modelo se ve obligado a priorizar los aspectos de la entrada que deben ser copiados, a menudo aprende propiedades útiles de los datos.
– Página 502, Aprendizaje profundo, 2016.
Los datos de entrada del dominio pueden entonces proporcionarse al modelo y la salida del modelo en el cuello de botella puede utilizarse como un vector de características en un modelo de aprendizaje supervisado, para la visualización o, más en general, para la reducción de la dimensionalidad.
A continuación, exploremos cómo podríamos desarrollar un autoencoder para la extracción de características en un problema de modelado predictivo de clasificación.
Autoencoder para la clasificación
En esta sección, desarrollaremos un autoencoder para aprender una representación comprimida de las características de entrada para un problema de modelado predictivo de clasificación.
Primero, definamos un problema de modelado predictivo de clasificación.
Utilizaremos la función make_classification() scikit-learn para definir una tarea de clasificación binaria sintética (de 2 clases) con 100 características de entrada (columnas) y 1.000 ejemplos (filas). Es importante que definamos el problema de tal manera que la mayoría de las variables de entrada sean redundantes (90 del 100 o 90 por ciento), permitiendo que el autoencoder aprenda más tarde una representación comprimida útil.
El ejemplo que figura a continuación define el conjunto de datos y resume su forma.
|
# Conjunto de datos de clasificación sintética de sklearn.conjuntos de datos importación hacer_clasificación # Definir el conjunto de datos X, y = make_classification(n_muestras=1000, n_funciones=100, n_informativo=10, n_redundante=90, estado_aleatorio=1) # resumir el conjunto de datos imprimir(X.forma, y.forma) |
Ejecutando el ejemplo se define el conjunto de datos y se imprime la forma de los conjuntos, confirmando el número de filas y columnas.
A continuación, desarrollaremos un modelo de autoencoder de Percepción Multicapa (MLP).
El modelo tomará todas las columnas de entrada, y luego producirá los mismos valores. Aprenderá a recrear el patrón de entrada exactamente.
El autoencoder consta de dos partes: el codificador y el decodificador. El codificador aprende a interpretar la entrada y a comprimirla en una representación interna definida por la capa del cuello de botella. El decodificador toma la salida del codificador (la capa de cuello de botella) e intenta recrear la entrada.
Una vez que el autoencoder es entrenado, el decodificador es descartado y sólo guardamos el codificador y lo usamos para comprimir los ejemplos de entrada a los vectores de salida por la capa de cuello de botella.
En este primer autocoder, no comprimiremos la entrada en absoluto y usaremos una capa de cuello de botella del mismo tamaño que la entrada. Esto debería ser un problema fácil que el modelo aprenderá casi a la perfección y tiene como objetivo confirmar que nuestro modelo se implementa correctamente.
Definiremos el modelo usando el API funcional; si esto es nuevo para usted, le recomiendo este tutorial:
Antes de definir y ajustar el modelo, dividiremos los datos en trenes y conjuntos de pruebas y escalaremos los datos de entrada normalizando los valores en el rango 0-1, una buena práctica con los MLP.
|
... # Dividido en conjuntos de prueba de trenes X_tren, X_test, y_tren, y_test = prueba_de_trenes_split(X, y, tamaño_de_prueba=0.33, estado_aleatorio=1) # datos de la escala t = MinMaxScaler() t.encajar(X_tren) X_tren = t.Transformar(X_tren) X_test = t.Transformar(X_test) |
Definiremos que el codificador tiene dos capas ocultas, la primera con dos veces el número de entradas (por ejemplo, 200) y la segunda con el mismo número de entradas (100), seguida de la capa de cuello de botella con el mismo número de entradas que el conjunto de datos (100).
Para asegurarnos de que el modelo aprende bien, usaremos la normalización de lotes y la activación de ReLU con fugas.
|
... # definir codificador visible = Entrada(forma=(n_inputs,)) # Nivel de codificador 1 e = Densa(n_inputs*2)(visible) e = BatchNormalization()(e) e = LeakyReLU()(e) # Nivel de codificador 2 e = Densa(n_inputs)(e) e = BatchNormalization()(e) e = LeakyReLU()(e) # cuello de botella n_bottleneck = n_inputs cuello de botella = Densa(n_bottleneck)(e) |
El decodificador se definirá con una estructura similar, aunque a la inversa.
Tendrá dos capas ocultas, la primera con el número de entradas en el conjunto de datos (por ejemplo, 100) y la segunda con el doble de entradas (por ejemplo, 200). La capa de salida tendrá el mismo número de nodos que hay columnas en los datos de entrada y utilizará una función de activación lineal para dar salida a los valores numéricos.
|
... # Definir el decodificador, nivel 1 d = Densa(n_inputs)(cuello de botella) d = BatchNormalization()(d) d = LeakyReLU()(d) # Nivel de decodificador 2 d = Densa(n_inputs*2)(d) d = BatchNormalization()(d) d = LeakyReLU()(d) # Capa de salida salida = Densa(n_inputs, activación=«lineal)(d) # Definir el modelo de autoencoder modelo = Modelo(aportaciones=visible, salidas=salida) |
El modelo se ajustará utilizando la versión eficiente de Adam de descenso de gradiente estocástico y minimiza el error cuadrático medio, dado que la reconstrucción es un tipo de problema de regresión multi-salida.
|
... # compilar el modelo de autoencoder modelo.compilar(optimizador=«adam, pérdida=«mse) |
Podemos trazar las capas en el modelo de auto-codificación para tener una idea de cómo los datos fluyen a través del modelo.
|
... # Trazar el autoencoder modelo_de_trama(modelo, ‘autoencoder_no_compress.png’, mostrar_formas=Verdadero) |
La imagen de abajo muestra un gráfico del autoencoder.
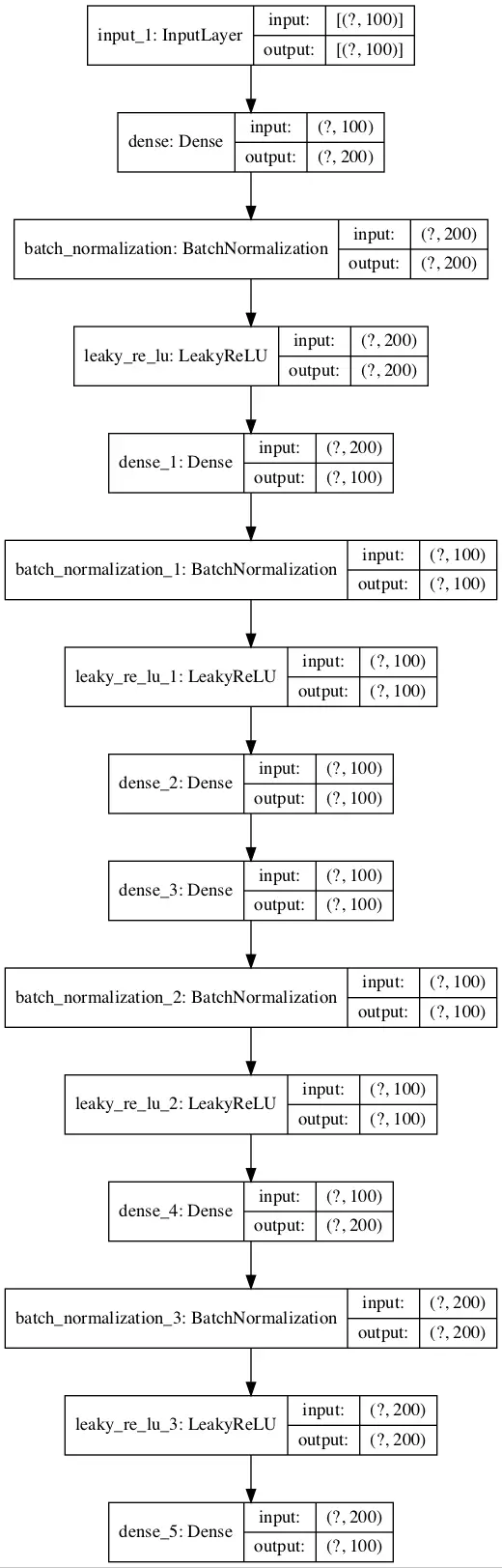
Esquema del modelo de autocodificador para la clasificación sin compresión
A continuación, podemos entrenar al modelo para reproducir la entrada y hacer un seguimiento del rendimiento del modelo en el conjunto de pruebas de retención.
|
... # Encajar el modelo de autoencoder para reconstruir la entrada historia = modelo.encajar(X_tren, X_tren, épocas=200, tamaño_de_lote=16, verboso=2, datos_de_validación=(X_test,X_test)) |
Después del entrenamiento, podemos trazar las curvas de aprendizaje del tren y los juegos de prueba para confirmar que el modelo aprendió bien el problema de la reconstrucción.
|
... # Pérdida de la trama pyplot.parcela(historia.historia[[«pérdida], etiqueta=«tren) pyplot.parcela(historia.historia[[‘val_loss’], etiqueta=«prueba) pyplot.leyenda() pyplot.mostrar() |
Por último, podemos guardar el modelo de codificador para usarlo más tarde, si se desea.
|
... # Definir un modelo de codificador (sin el decodificador) codificador = Modelo(aportaciones=visible, salidas=cuello de botella) modelo_de_trama(codificador, ‘encoder_no_comprimir.png’, mostrar_formas=Verdadero) # Guarda el codificador en un archivo codificador.guardar(«codificador.h5) |
Como parte de guardar el codificador, también trazaremos el modelo del codificador para tener una idea de la forma de la salida de la capa de cuello de botella, por ejemplo, un vector de 100 elementos.
A continuación se presenta un ejemplo de esta trama.
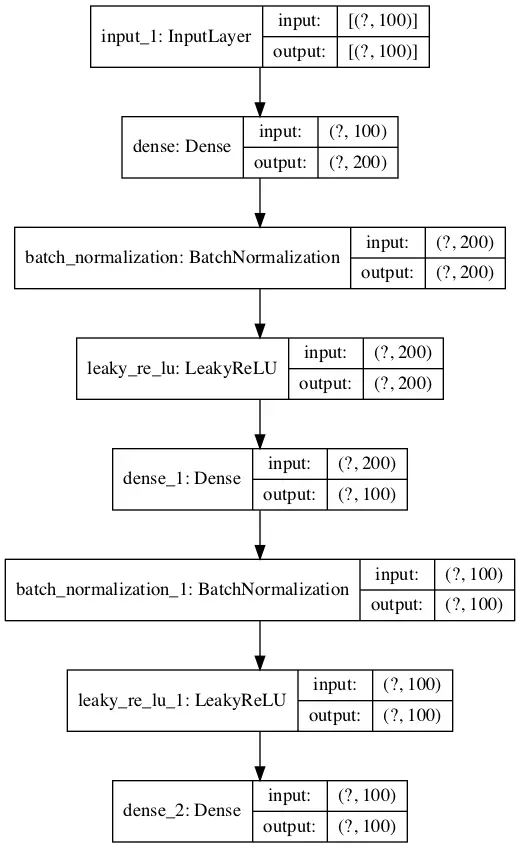
Esquema del modelo de codificador para la clasificación sin compresión
Enlazando todo esto, el ejemplo completo de un autoencoder para reconstruir los datos de entrada para un conjunto de datos de clasificación sin ninguna compresión en la capa de cuello de botella se enumera a continuación.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 |
# Tren de autoencoder para la clasificación sin compresión en la capa del cuello de botella de sklearn.conjuntos de datos importación make_classification de sklearn.preprocesamiento importación MinMaxScaler de sklearn.model_selection importación prueba_de_trenes_split de tensorflow.keras.modelos importación Modelo de tensorflow.keras.capas importación Entrada de tensorflow.keras.capas importación Densa de tensorflow.keras.capas importación LeakyReLU de tensorflow.keras.capas importación BatchNormalization de tensorflow.keras.utils importación modelo_de_trama de matplotlib importación pyplot # Definir el conjunto de datos X, y = make_classification(n_muestras=1000, n_funciones=100, n_informativo=10, n_redundante=90, estado_aleatorio=1) # Número de columnas de entrada n_inputs = X.forma[[1] # Dividido en conjuntos de prueba de trenes X_tren, X_test, y_tren, y_test = prueba_de_trenes_split(X, y, tamaño_de_prueba=0.33, estado_aleatorio=1) # datos de la escala t = MinMaxScaler() t.encajar(X_tren) X_tren = t.Transformar(X_tren) X_test = t.Transformar(X_test) # definir codificador visible = Entrada(forma=(n_inputs,)) # Nivel de codificador 1 e = Densa(n_inputs*2)(visible) e = BatchNormalization()(e) e = LeakyReLU()(e) # Nivel de codificador 2 e = Densa(n_inputs)(e) e = BatchNormalization()(e) e = LeakyReLU()(e) # cuello de botella n_bottleneck = n_inputs cuello de botella = Densa(n_bottleneck)(e) # Definir el decodificador, nivel 1 d = Densa(n_inputs)(cuello de botella) d = BatchNormalization()(d) d = LeakyReLU()(d) # Nivel de decodificador 2 d = Densa(n_inputs*2)(d) d = BatchNormalization()(d) d = LeakyReLU()(d) # Capa de salida salida = Densa(n_inputs, activación=«lineal)(d) # Definir el modelo de autoencoder modelo = Modelo(aportaciones=visible, salidas=salida) # compilar el modelo de autoencoder modelo.compilar(optimizador=«adam, pérdida=«mse) # Trazar el autoencoder modelo_de_trama(modelo, ‘autoencoder_no_compress.png’, mostrar_formas=Verdadero) # Encajar el modelo de autoencoder para reconstruir la entrada historia = modelo.encajar(X_tren, X_tren, épocas=200, tamaño_de_lote=16, verboso=2, datos_de_validación=(X_test,X_test)) # Pérdida de la trama pyplot.parcela(historia.historia[[«pérdida], etiqueta=«tren) pyplot.parcela(historia.historia[[‘val_loss’], etiqueta=«prueba) pyplot.leyenda() pyplot.mostrar() # Definir un modelo de codificador (sin el decodificador) codificador = Modelo(aportaciones=visible, salidas=cuello de botella) modelo_de_trama(codificador, ‘encoder_no_comprimir.png’, mostrar_formas=Verdadero) # Guarda el codificador en un archivo codificador.guardar(«codificador.h5) |
Ejecutando el ejemplo se ajusta al modelo e informa de la pérdida en el tren y los juegos de prueba a lo largo del camino.
Notasi tienes problemas para crear las tramas del modelo, puedes comentar la importación y llamar al plot_model() función.
Nota: Sus resultados pueden variar dada la naturaleza estocástica del algoritmo o el procedimiento de evaluación, o las diferencias en la precisión numérica. Considere ejecutar el ejemplo unas cuantas veces y compare el resultado promedio.
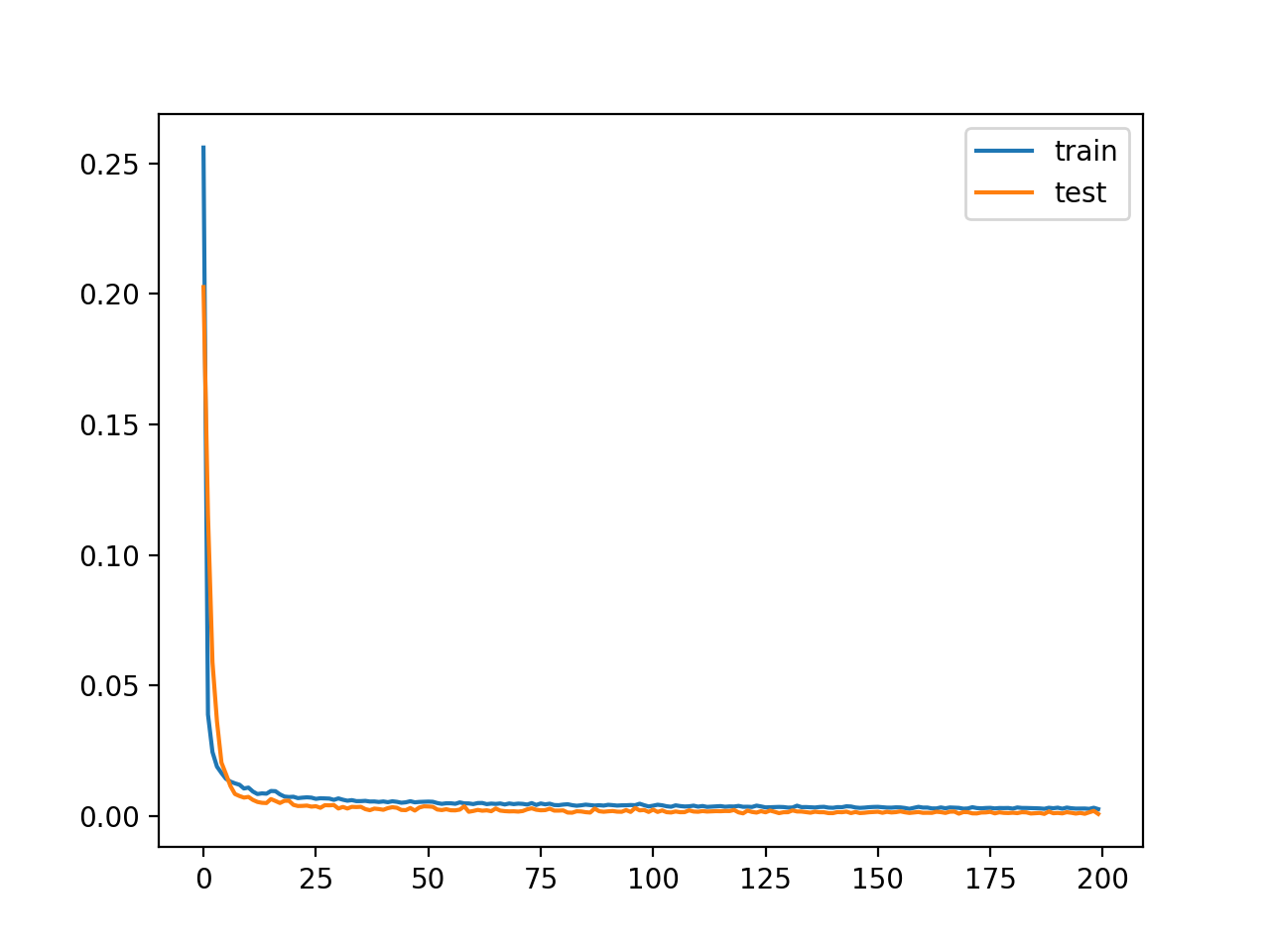
En este caso, vemos que la pérdida es baja, pero no llega a cero (como podíamos haber esperado) sin compresión en la capa del cuello de botella. Tal vez se requiera un mayor ajuste de la arquitectura del modelo o el aprendizaje de hiperparámetros.
|
… 42/42 – 0s – pérdida: 0.0032 – val_loss: 0.0016 Época 196/200 42/42 – 0s – pérdida: 0.0031 – val_loss: 0.0024 Época 197/200 42/42 – 0s – pérdida: 0.0032 – val_loss: 0.0015 Época 198/200 42/42 – 0s – pérdida: 0.0032 – val_loss: 0.0014 Época 199/200 42/42 – 0s – pérdida: 0.0031 – val_loss: 0.0020 Época 200/200 42/42 – 0s – pérdida: 0.0029 – val_loss: 0.0017 |
Se crea un gráfico de las curvas de aprendizaje que muestra que el modelo logra un buen ajuste en la reconstrucción de la entrada, que se mantiene constante a lo largo del entrenamiento, no en exceso.
Curvas de aprendizaje del modelo de autoencoder sin compresión
Hasta ahora, todo bien. Sabemos cómo desarrollar un autoencoder sin compresión.
A continuación, cambiemos la configuración del modelo para que la capa de cuello de botella tenga la mitad del número de nodos (por ejemplo, 50).
|
... # cuello de botella n_bottleneck = ronda(flotación(n_inputs) / 2.0) cuello de botella = Densa(n_bottleneck)(e) |
A continuación se muestra el ejemplo completo.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 |
# Tren autocodificador para la clasificación con compresión en la capa del cuello de botella de sklearn.conjuntos de datos importación make_classification de sklearn.preprocesamiento importación MinMaxScaler de sklearn.model_selection importación prueba_de_trenes_split de tensorflow.keras.modelos importación Modelo de tensorflow.keras.capas importación Entrada de tensorflow.keras.capas importación Densa de tensorflow.keras.capas importación LeakyReLU de tensorflow.keras.capas importación BatchNormalization de tensorflow.keras.utils importación modelo_de_trama de matplotlib importación pyplot # Definir el conjunto de datos X, y = make_classification(n_muestras=1000, n_funciones=100, n_informativo=10, n_redundante=90, estado_aleatorio=1) # Número de columnas de entrada n_inputs = X.forma[[1] # Dividido en conjuntos de prueba de trenes X_tren, X_test, y_tren, y_test = prueba_de_trenes_split(X, y, tamaño_de_prueba=0.33, estado_aleatorio=1) # datos de la escala t = MinMaxScaler() t.encajar(X_tren) X_tren = t.Transformar(X_tren) X_test = t.Transformar(X_test) # definir codificador visible = Entrada(forma=(n_inputs,)) # Nivel de codificador 1 e = Densa(n_inputs*2)(visible) e = BatchNormalization()(e) e = LeakyReLU()(e) # Nivel de codificador 2 e = Densa(n_inputs)(e) e = BatchNormalization()(e) e = LeakyReLU()(e) # cuello de botella n_bottleneck = ronda(flotación(n_inputs) / 2.0) cuello de botella = Densa(n_bottleneck)(e) # Definir el decodificador, nivel 1 d = Densa(n_inputs)(cuello de botella) d = BatchNormalization()(d) d = LeakyReLU()(d) # Nivel de decodificador 2 d = Densa(n_inputs*2)(d) d = BatchNormalization()(d) d = LeakyReLU()(d) # Capa de salida salida = Densa(n_inputs, activación=«lineal)(d) # Definir el modelo de autoencoder modelo = Modelo(aportaciones=visible, salidas=salida) # compilar el modelo de autoencoder modelo.compilar(optimizador=«adam, pérdida=«mse) # Trazar el autoencoder modelo_de_trama(modelo, ‘autoencoder_compress.png’, mostrar_formas=Verdadero) # Encajar el modelo de autoencoder para reconstruir la entrada historia = modelo.encajar(X_tren, X_tren, épocas=200, tamaño_de_lote=16, verboso=2, datos_de_validación=(X_test,X_test)) # Pérdida de la trama pyplot.parcela(historia.historia[[«pérdida], etiqueta=«tren) pyplot.parcela(historia.historia[[‘val_loss’], etiqueta=«prueba) pyplot.leyenda() pyplot.mostrar() # Definir un modelo de codificador (sin el decodificador) codificador = Modelo(aportaciones=visible, salidas=cuello de botella) modelo_de_trama(codificador, ‘encoder_compress.png’, mostrar_formas=Verdadero) # Guarda el codificador en un archivo codificador.guardar(«codificador.h5) |
Ejecutando el ejemplo se ajusta al modelo e informa de la pérdida en el tren y los juegos de prueba a lo largo del camino.
Nota: Sus resultados pueden variar dada la naturaleza estocástica del algoritmo o el procedimiento de evaluación, o las diferencias en la precisión numérica. Considere ejecutar el ejemplo unas cuantas veces y compare el resultado promedio.
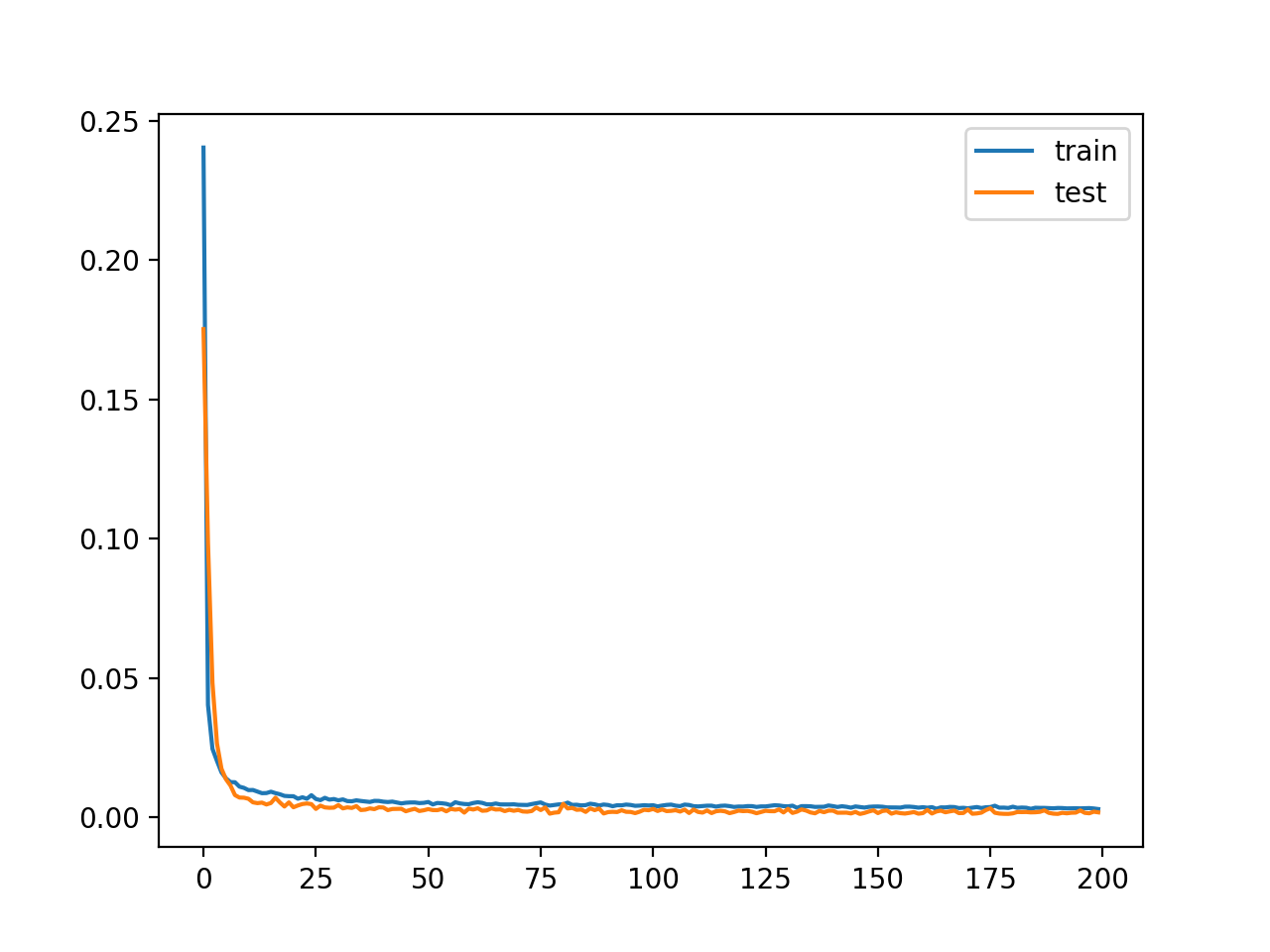
En este caso, vemos que la pérdida se reduce de manera similar a la del ejemplo anterior sin compresión, lo que sugiere que tal vez el modelo funciona igual de bien con un cuello de botella de la mitad del tamaño.
|
… 42/42 – 0s – pérdida: 0.0029 – val_loss: 0.0010 Época 196/200 42/42 – 0s – pérdida: 0.0029 – val_loss: 0.0013 Época 197/200 42/42 – 0s – pérdida: 0.0030 – val_loss: 9.4472e-04 Época 198/200 42/42 – 0s – pérdida: 0.0028 – val_loss: 0.0015 Época 199/200 42/42 – 0s – pérdida: 0.0033 – val_loss: 0.0021 Época 200/200 42/42 – 0s – pérdida: 0.0027 – val_loss: 8.7731e-04 |
Se crea un gráfico de las curvas de aprendizaje, mostrando de nuevo que el modelo logra un buen ajuste en la reconstrucción de la entrada, que se mantiene constante a lo largo del entrenamiento, no en exceso.

Curvas de aprendizaje del modelo de autocodificador con compresión
El codificador entrenado se guarda en el archivo «codificador.h5«que podemos cargar y usar más tarde.
A continuación, exploremos cómo podríamos usar el modelo de codificador entrenado.
El codificador como preparación de datos para el modelo de predicción
En esta sección, usaremos el codificador entrenado del autoencoder para comprimir los datos de entrada y entrenar un modelo predictivo diferente.
Primero, establezcamos una línea de base en el desempeño de este problema. Esto es importante, ya que si el rendimiento de un modelo no mejora con la codificación comprimida, entonces la codificación comprimida no añade valor al proyecto y no debe utilizarse.
Podemos entrenar un modelo de regresión logística en el conjunto de datos de entrenamiento directamente y evaluar el rendimiento del modelo en el conjunto de pruebas de retención.
El ejemplo completo figura a continuación.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 |
# línea de base en el desempeño con el modelo de regresión logística de sklearn.conjuntos de datos importación make_classification de sklearn.preprocesamiento importación MinMaxScaler de sklearn.preprocesamiento importación LabelEncoder de sklearn.model_selection importación prueba_de_trenes_split de sklearn.modelo_lineal importación LogisticRegression de sklearn.métrica importación exactitud_puntuación # Definir el conjunto de datos X, y = make_classification(n_muestras=1000, n_funciones=100, n_informativo=10, n_redundante=90, estado_aleatorio=1) # Dividido en conjuntos de prueba de trenes X_tren, X_test, y_tren, y_test = prueba_de_trenes_split(X, y, tamaño_de_prueba=0.33, estado_aleatorio=1) # datos de la escala t = MinMaxScaler() t.encajar(X_tren) X_tren = t.Transformar(X_tren) X_test = t.Transformar(X_test) # Definir el modelo modelo = LogisticRegression() # Modelo de ajuste en el set de entrenamiento modelo.encajar(X_tren, y_tren) # Hacer la predicción en el equipo de pruebas yhat = modelo.predecir(X_test) # calcular la precisión acc = accuracy_score(y_test, yhat) imprimir(acc) |
La ejecución del ejemplo se ajusta a un modelo de regresión logística en el conjunto de datos de entrenamiento y lo evalúa en el conjunto de pruebas.
Nota: Sus resultados pueden variar dada la naturaleza estocástica del algoritmo o el procedimiento de evaluación, o las diferencias en la precisión numérica. Considere ejecutar el ejemplo unas cuantas veces y compare el resultado promedio.
En este caso, podemos ver que el modelo logra una precisión de clasificación de alrededor del 89,3 por ciento.
Esperamos y deseamos que un modelo de regresión logística se ajuste a una versión codificada de la entrada para lograr una mayor precisión para que la codificación se considere útil.
Podemos actualizar el ejemplo para codificar primero los datos utilizando el modelo de codificador entrenado en la sección anterior.
Primero, podemos cargar el modelo de codificador entrenado desde el archivo.
|
... # Cargar el modelo desde el archivo codificador = load_model(«codificador.h5) |
Podemos entonces utilizar el codificador para transformar los datos de entrada en bruto (por ejemplo, 100 columnas) en vectores de cuello de botella (por ejemplo, 50 vectores de elementos).
Este proceso puede aplicarse al tren y a los conjuntos de datos de prueba.
|
... # codificar los datos del tren X_código_de_trenes = codificador.predecir(X_tren) # codificar los datos de la prueba X_test_encode = codificador.predecir(X_test) |
Podemos entonces usar estos datos codificados para entrenar y evaluar el modelo de regresión logística, como antes.
|
... # Definir el modelo modelo = LogisticRegression() # Encajar el modelo en el set de entrenamiento modelo.encajar(X_código_de_trenes, y_tren) # hacer predicciones en el conjunto de pruebas yhat = modelo.predecir(X_test_encode) |
A continuación se muestra el ejemplo completo.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 |
# Evaluar la regresión logística en la entrada codificada de sklearn.conjuntos de datos importación make_classification de sklearn.preprocesamiento importación MinMaxScaler de sklearn.preprocesamiento importación LabelEncoder de sklearn.model_selection importación prueba_de_trenes_split de sklearn.modelo_lineal importación LogisticRegression de sklearn.métrica importación accuracy_score de tensorflow.keras.modelos importación carga_modelo # Definir el conjunto de datos X, y = make_classification(n_muestras=1000, n_funciones=100, n_informativo=10, n_redundante=90, estado_aleatorio=1) # Dividido en conjuntos de prueba de trenes X_tren, X_test, y_tren, y_test = prueba_de_trenes_split(X, y, tamaño_de_prueba=0.33, estado_aleatorio=1) # datos de la escala t = MinMaxScaler() t.encajar(X_tren) X_tren = t.Transformar(X_tren) X_test = t.Transformar(X_test) # Cargar el modelo desde el archivo codificador = load_model(«codificador.h5) # codificar los datos del tren X_código_de_trenes = codificador.predecir(X_tren) # codificar los datos de la prueba X_test_encode = codificador.predecir(X_test) # Definir el modelo modelo = LogisticRegression() # Encajar el modelo en el set de entrenamiento modelo.encajar(X_código_de_trenes, y_tren) # hacer predicciones en el conjunto de pruebas yhat = modelo.predecir(X_test_encode) # Calcular la precisión de la clasificación acc = accuracy_score(y_test, yhat) imprimir(acc) |
La ejecución del ejemplo primero codifica el conjunto de datos utilizando el codificador, luego ajusta un modelo de regresión logística en el conjunto de datos de entrenamiento y lo evalúa en el conjunto de pruebas.
Nota: Sus resultados pueden variar dada la naturaleza estocástica del algoritmo o el procedimiento de evaluación, o las diferencias en la precisión numérica. Considere ejecutar el ejemplo unas cuantas veces y compare el resultado promedio.
En este caso, podemos ver que el modelo logra una precisión de clasificación de alrededor del 93,9 por ciento.
Esta es una mejor precisión de clasificación que el mismo modelo evaluado en el conjunto de datos en bruto, lo que sugiere que la codificación es útil para nuestro modelo elegido y el arnés de prueba.
Más lecturas
Esta sección proporciona más recursos sobre el tema si desea profundizar en él.
Tutoriales
Libros
APIs
Artículos
Resumen
En este tutorial, descubriste cómo desarrollar y evaluar un autoencoder para el modelado predictivo de clasificación.
Específicamente, aprendiste:
- Un autoencoder es un modelo de red neuronal que puede ser usado para aprender una representación comprimida de los datos en bruto.
- Cómo entrenar un modelo de autoencoder en un conjunto de datos de entrenamiento y guardar sólo la parte de codificador del modelo.
- Cómo usar el codificador como un paso de preparación de datos cuando se entrena un modelo de aprendizaje de una máquina.
¿Tiene alguna pregunta?
Haga sus preguntas en los comentarios de abajo y haré lo posible por responder.

