La tasa de letalidad cuantifica lo peligroso que es COVID-19, y cómo el riesgo de muerte varía con los estratos
como la geografía, la edad y la raza. Las estimaciones actuales de la tasa de mortalidad de los casos de COVID-19 (CFR) están sesgadas
por docenas de razones, desde la falta de pruebas en casos asintomáticos hasta la información errónea del gobierno. Nosotros proveemos
una cuidadosa y completa visión general de estos sesgos y mostrar cómo el pensamiento estadístico y el modelado pueden
combatir esos problemas. Lo más importante es que la calidad de los datos es clave para la estimación imparcial de la CFR. Mostramos que un
El conjunto de datos relativamente pequeño recogido mediante un cuidadoso rastreo de contactos permitiría una simple y potencialmente más
una estimación precisa de la CFR.
La tasa de letalidad (CFR) es la proporción de casos fatales de COVID-19. El término es ambiguo,
ya que su valor depende de la definición de un «caso». No hay una definición perfecta del caso
la tasa de mortalidad existe, pero en este artículo, la defino vagamente como la proporción de muertes entre todos los
Individuos infectados con COVID-19.
El CFR es una medida de la gravedad de la enfermedad. Además, el CFR relativo (la proporción de CFR
entre dos subpoblaciones) permite la asignación de recursos basada en datos
mediante la cuantificación del riesgo relativo. En otras palabras, el CFR nos dice lo drástica que es nuestra respuesta
necesita ser; el relativo CFR nos ayuda a asignar los escasos recursos a las poblaciones que tienen un
un mayor riesgo de muerte.
Aunque el CFR se define como el número de infecciones mortales, no podemos
esperar que dividiendo el número de muertes por el número de casos nos dé una
una buena estimación de la CFR. El problema es que tanto el numerador (#muertos) como
el denominador (#infecciones) de esta fracción son inciertas para la sistemática
por la forma en que se recogen los datos. Por esta razón, llamamos a eso
estimador «el ingenuo estimador«, o simplemente muertes/casos…y denotarlo como $E_{N- Ingenuo}$.
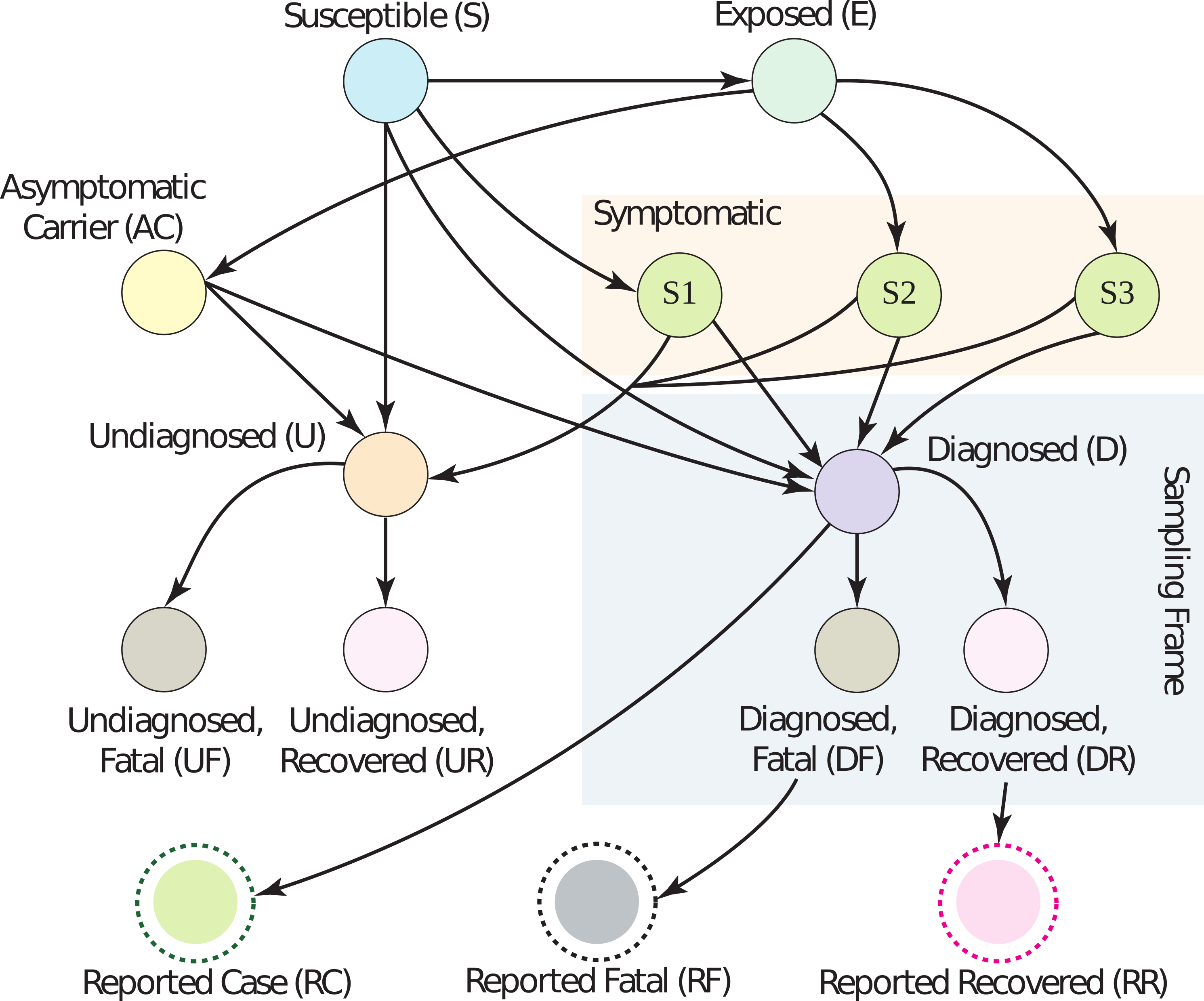
Docenas de sesgos pueden corromper la estimación del CFR. Los datos de vigilancia
da información parcial dentro del «marco de muestreo» (rectángulo azul claro). Los bordes de
el gráfico corresponde aproximadamente a las probabilidades condicionales; por ejemplo, el borde de D a DF
es la probabilidad de que una persona muera si se le diagnostica COVID-19.
En resumen, todas las estimaciones de CFR están sesgadas porque los datos disponibles públicamente están sesgados.
Tenemos razones para creer que estamos perdiendo al menos el 99,8% de nuestra eficiencia de la muestra debido a este sesgo.
Hay un «efecto mariposa» causado por el muestreo no aleatorio: una pequeña correlación entre el
de muestreo y la cantidad de interés puede tener enormes efectos destructivos en una
estimador. Incluso asumiendo una diminuta correlación de 0,005 entre la población que probamos y el
población infectada, la prueba de 10.000 personas para el SARS-CoV-2 es equivalente a la prueba del 20
individuos al azar. Para estimar la tasa de mortalidad, la situación es aún peor,
ya que tenemos amplias pruebas de que los casos graves se diagnostican preferentemente y
reportado. En palabras de Xiao-Li Meng, «compensar por [data] la calidad con la cantidad es
un juego condenado». En nuestro artículo de HDSR, mostramos que para que el estimador ingenuo $E_{\N- ingenuo}$ converja
a la correcta CFR, no debe haber ninguna correlación entre la fatalidad y ser probado – pero
Los casos graves tienen muchas más probabilidades de ser examinados. El gobierno y las organizaciones de salud han
reservando explícitamente las pruebas para los casos graves debido a la escasez, y es probable que los casos graves vayan
…al hospital y hacerse las pruebas, mientras que los asintomáticos no lo son.
La fuente principal de los datos de COVID-19 es la vigilancia de la población: agregado a nivel de condado
estadísticas reportadas por los proveedores médicos que diagnostican a los pacientes en el lugar. Normalmente, alguien
se sienten enfermos y van a un hospital, donde se les hacen pruebas y se les diagnostica. El hospital informa que el
número de casos, muertes y a veces recuperaciones a las autoridades locales, que publican los datos
sobre una base semanal. En realidad, hay muchas diferencias
en la recopilación de datos entre las naciones, los gobiernos locales e incluso los hospitales.
Este método de vigilancia induce docenas de sesgos, que se pueden clasificar en cinco categorías:
insuficiencia de casos leves, desfases temporales, intervenciones, características del grupo (por ejemplo
edad, sexo, raza), y notificación y atribución imperfectas. Una discusión extensa (pero no exhaustiva)
de la magnitud y dirección de estos sesgos está en la Sección 2 de nuestro artículo. Sin rodeos, los datos actuales
es de muy baja calidad. La gran mayoría de las personas que contraen COVID-19 no son diagnosticadas, hay
atribuciones erróneas de los síntomas y las muertes, los datos comunicados por los gobiernos son a menudo (y tal vez a propósito)
incorrecta, los casos se definen de manera inconsistente en los distintos países, y hay muchos desfases temporales. (Por ejemplo,
los casos se cuentan como «diagnosticados» antes de que sean «fatales», lo que lleva a un sesgo descendente en el CFR si el
el número de casos está creciendo con el tiempo). Figura 1 tiene un modelo gráfico que describe estas muchas relaciones;
mira el papel para una explicación detallada de los sesgos que ocurren a través de cada borde.
A veces es posible corregir los sesgos utilizando fuentes de datos externas, pero puede dar lugar a una peor
estimador en general debido a la cancelación parcial del sesgo. Esto es más fácil de ver a través del ejemplo que de explicar.
Supongamos que el verdadero CFR es algún valor $p$ en el rango de 0 a 1 (es decir, las muertes/infecciones es igual a $p$). Entonces,
asumen que debido a la escasez de casos leves, hay demasiados casos fatales reportados, los cuales
significa que $E_{rm ingenuo}$ converge en $bp > p$ (en otras palabras, es más alto de lo que debería ser por un factor de $b$).
También se supone que el lapso de tiempo entre el diagnóstico y la muerte causa la proporción de
las muertes a los diagnósticos para disminuir por el mismo factor $b$. Entonces, $E_{\N- Ingenuo}$ converge en $b(p/b)=p$,
el valor correcto. Así que, aunque podría parecer una buena idea objetiva corregir el desfase temporal entre
diagnóstico y muerte, en realidad resultaría en un peor estimador en este caso, ya que el desfase temporal nos está ayudando
anulando la falta de seguridad.
La forma matemática del estimador ingenuo $E_{rm ingenuo}$ nos permite ver fácilmente lo que tenemos que hacer para que sea imparcial.
Con $p$ siendo el verdadero CFR, $q$ siendo la tasa de reporte, y $r$ siendo la covarianza entre la muerte y el diagnóstico,
la media de $E_{\N- Ingenuo}$ es:
Esta ecuación es bastante fácil de entender. Queríamos que $mu$ fuera igual a $p$. En lugar de eso, conseguimos una expresión
que depende de $r$, $q$, y $N$. El término $r/q$ es el precio que pagamos si las personas que son diagnosticadas son más propensas
para eventualmente morir. Queremos $r/q=0$, pero en la práctica, $r/q$ es probablemente mucho más grande que $p$. (En realidad, si
asumiendo que el CFR es de alrededor de 0,5% y el CFR medido es de 5,2% el 22 de junio de 2020, entonces $r/q ge 0,047 gg 0,005$.) En
En otras palabras, $r/q$ es el sesgo, y puede ser grande. El término $p$ es el verdadero CFR, el cual queremos.
Y el factor $(1-(1-q)^N)$ es lo que pagamos por la falta de respuesta; sin embargo, no es gran cosa, porque
desaparece bastante rápido a medida que el número de muestras $N$ crece. Así que realmente, nuestra principal preocupación debería ser
logrando $r=0$, porque – y no puedo enfatizar esto lo suficiente – $r/q$ no disminuye con más muestras;
sólo disminuye con muestras de mayor calidad.
En nuestro artículo, esbozamos un procedimiento de prueba que ayuda a arreglar algunos de los sesgos del conjunto de datos anteriores. Si nosotros
recoger los datos adecuadamente, incluso el estimador ingenuo $E_{\N- ingenuo}$ tiene un buen rendimiento.
En particular, los datos deben recopilarse mediante un procedimiento como el siguiente:
- Diagnosticar a la persona $P$ con COVID-19 por cualquier medio, como en un hospital.
- Alcanza a los contactos de $P$. Si un contacto no tiene síntomas, pídales que se comprometan a hacerse una prueba de COVID-19.
- Pruebe los contactos comprometidos después de que el virus se haya incubado.
- Mantener los datos con la máxima granularidad respetando la ética y la ley.
- Seguimiento después de unas semanas para determinar la gravedad de los síntomas.
- Para los contactos comprometidos que no se hayan hecho la prueba, llamen y anoten si son asintomáticos.
Este protocolo tiene como objetivo disminuir la covarianza entre la fatalidad y el diagnóstico. Si los pacientes se comprometen a
antes de que desarrollen los síntomas, esta covarianza simplemente no puede existir.
Sin embargo, todavía puede haber problemas con las personas que abandonan el estudio; si esto es un problema en la práctica,
puede mitigarse mediante una combinación de incentivos (pagos) y seguimientos constantes.
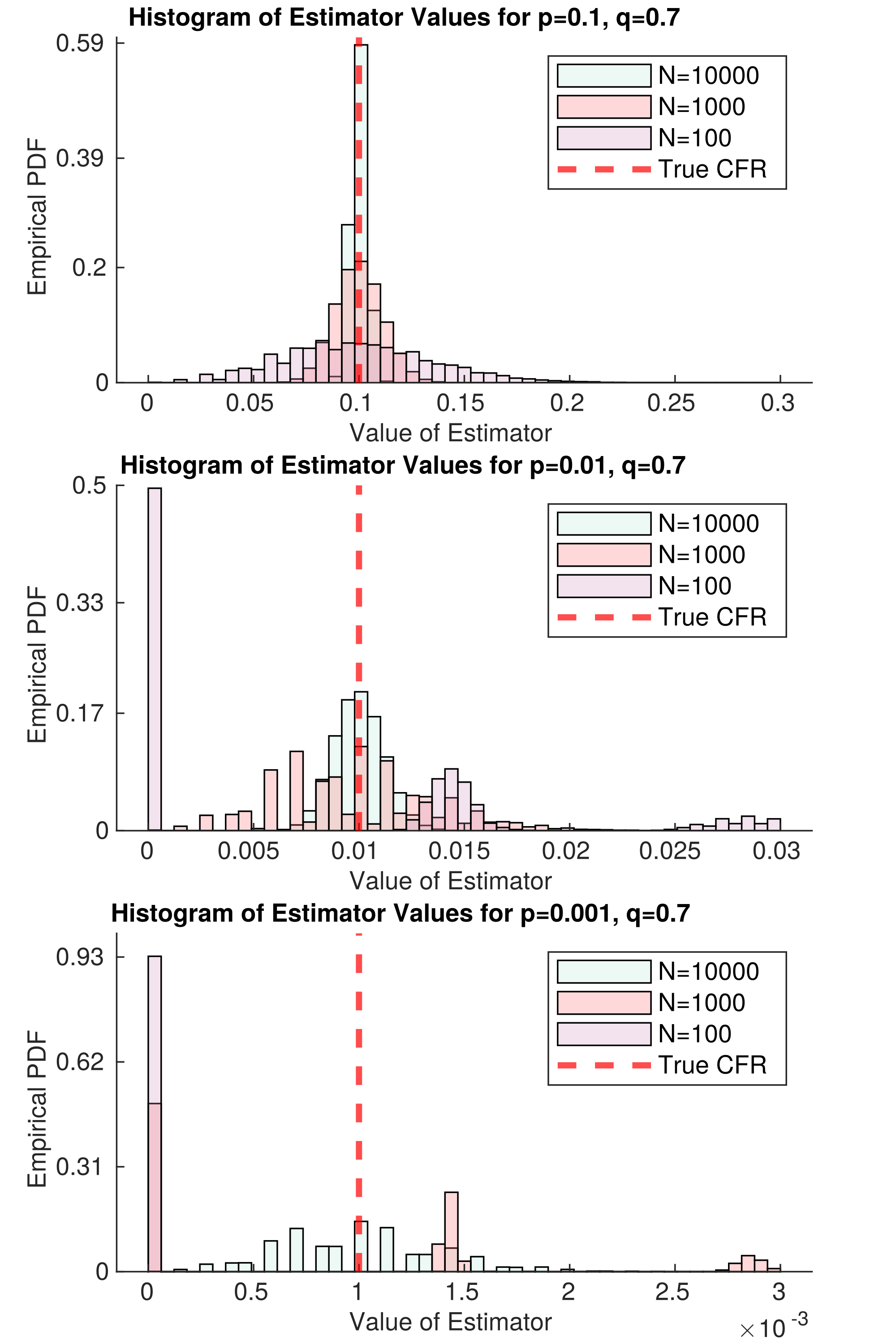Fig. 2 Asumiendo que la recolección de datos no induce a una correlación entre la gravedad de la enfermedad y el diagnóstico, ya que la verdadera CFR disminuye,requiere más muestras para estimar. La variable p es el verdadero CFR, y q es la tasa de respuesta. Cada histograma representa
la probabilidad de que el estimador ingenuo tome un cierto valor, dada N muestras de datos (diferentes colores corresponden a diferentes
valores de N). Las tres parcelas apiladas corresponden a diferentes valores de p…el más pequeño… p es, más difícil de estimar,
ya que la muerte se convierte en un evento extremadamente raro.
Figura 2 representa una versión idealizada de este estudio. En el mejor de los casos, no hay
covarianza entre la muerte y el diagnóstico. Entonces, sólo necesitamos muestras de $N=66$ para nuestra
estimador del CFR sea aproximadamente imparcial, incluso si $p=0.001$ ($1/1000$ los casos mueren). Problemas
permanecen en el caso de que $p$ sea pequeño; es decir, la muerte es tan rara que necesitamos toneladas de muestras para
disminuir la varianza de nuestro estimador. Esto requerirá muchas muestras. Pero incluso si no hay muertes
se observan, obtenemos mucha información sobre $p$; por ejemplo, si $N=1000$ y nosotros
no han observado ni una sola muerte, entonces podemos decir con confianza que $p<0.01$ dentro de la
población que estamos muestreando. Esto es simplemente porque en el segundo panel de Figura 2,
hay casi cero masa en el histograma de $N=1000$ a $E_{rm ingenuo} = 0$. Con esto en mente, podríamos
encontrar la mayor p posible que sea consistente con nuestros datos – esto sería un conservador superior
…pero estaría mucho más cerca del valor real de lo que podemos obtener con los datos actuales.
Esta estrategia resuelve lo que creemos que es el mayor conjunto de sesgos en la estimación de la CFR…
…de casos leves y retrasos. Sin embargo, todavía habrá mucho espacio para
como entender la dependencia de la CFR de la edad, el sexo y la raza. (En otras palabras,
la CFR es una cantidad aleatoria en sí misma, dependiendo de la población que se muestreeó). Distinciones
entre los CFR de estos estratos puede ser bastante pequeño, requiriendo una gran cantidad de datos de alta calidad para
Analizar. Si $p$ es extremadamente bajo, como 0.001,
esto puede requerir la recolección de muestras de $N=100.000$ o $N=1.000.000$ por grupo. Tal vez
hay formas de reducir ese número reuniendo muestras. Aunque hacer
las inferencias correctas requerirán un pensamiento cuidadoso (como siempre), esta estrategia de recolección de datos
lo hará mucho más simple.
Me gustaría volver a subrayar un punto aquí: la recogida de datos como arriba hará que el estimador ingenuo $E_{rm ingenuo}$
imparcial para la población de la muestra. Pero la población muestreada puede no ser la población
que nos importa. Sin embargo, hay un conjunto de técnicas estadísticas llamadas colectivamente
«post estratificación» que puede ayudar a tratar este problema de manera efectiva – véase el Sr. P.
Si lee nuestro artículo académico, le proporcionamos algunas ideas sobre cómo utilizar los datos de las series temporales
e información externa para corregir los desfases temporales y las tasas relativas de presentación de informes. Nuestro trabajo fue muy
basado en gran medida en uno de los documentos de Nick Reich. Sin embargo, como he dicho antes, incluso la fantasía
los estimadores no pueden superar los problemas fundamentales de la recopilación de datos. Aplazaré la discusión de
ese estimador, y los resultados que obtuvimos de él, al artículo. Me encantaría escuchar
tus pensamientos sobre ello.
La estimación de la CFR es claramente un problema difícil, pero con una adecuada recopilación de datos y
estimación guiada por los científicos de datos, todavía creo que podemos obtener una útil estimación de CFR.
Esto ayudará a orientar las decisiones de política pública sobre esta urgente y continua pandemia.
Esta entrada en el blog se basa en el siguiente documento: