Entrenamiento en pruebas de entrada con probabilidad máxima condicional normalizada amortizada – El blog de investigación de inteligencia artificial de Berkeley

Los actuales métodos de aprendizaje de la máquina proporcionan una precisión sin precedentes en toda una gama
de dominios, desde la visión de la computadora hasta el procesamiento del lenguaje natural. Sin embargo, en
muchas aplicaciones importantes de alto riesgo, como el diagnóstico médico o
conducción autónoma, los errores raros pueden ser extremadamente costosos, y por lo tanto efectivos
El despliegue de los modelos aprendidos requiere no sólo una gran precisión, sino también una forma de
medir la certeza en las predicciones de un modelo. La incertidumbre fiable
La cuantificación es especialmente importante cuando se enfrenta a la falta de distribución
ya que la precisión del modelo tiende a degradarse mucho en las entradas que difieren
significativamente de los que se vieron durante el entrenamiento. En esta entrada del blog, vamos a
discutir cómo podemos obtener una estimación fiable de la incertidumbre con una estrategia que
no se basa simplemente en un modelo aprendido para extrapolar a la distribución exterior
de entrada, pero en vez de eso pregunta: «Dados los datos de mi formación, ¿qué etiquetas harían
sentido para esta entrada?».

Para ilustrar cómo esto puede permitir predicciones más razonables sobre
datos fuera de distribución, considere el siguiente ejemplo en el que intentamos
clasificar los automóviles, donde todos los ejemplos de entrenamiento de clase 1 son sedanes y
Los ejemplos de la clase 2 son los autobuses grandes.

Figura 1: Dados los ejemplos vistos anteriormente, es incierto cuál es la etiqueta para
el nuevo punto de consulta debería ser. Diferentes clasificadores que funcionan bien en el
El conjunto de entrenamiento puede dar diferentes predicciones sobre el punto de consulta.

Un clasificador podría potencialmente encajar las etiquetas de entrenamiento correctamente basado en
varias explicaciones diferentes; por ejemplo, podría notar que los autobuses son todos
más largo que los sedanes y clasificar en consecuencia, o tal vez podría prestar atención
a la altura del vehículo en su lugar. Sin embargo, si intentamos simplemente extrapolar
a una imagen de una limusina fuera de distribución, la salida del clasificador podría
ser impredecible y arbitrario. Un clasificador basado en la longitud podría observar que
la limusina es similar a los autobuses en su longitud y predecir con confianza
clase 2, mientras que un clasificador que utiliza la altura podría predecir con confianza
clase 1. Basándonos sólo en el conjunto de entrenamiento, no hay suficiente información para
decidir con precisión en qué clase de limusina debería caber, por lo que lo ideal sería
quieren que nuestro clasificador indique la incertidumbre en lugar de proporcionar una arbitraria
predicciones confiables para cualquiera de las dos clases. Por otro lado, si intentamos explícitamente
para encontrar modelos que expliquen cada etiqueta potencial, encontraríamos razonable
explicaciones para cualquiera de las dos etiquetas, lo que sugiere que deberíamos tener dudas sobre
prediciendo a qué clase pertenece la limusina.

Podemos instanciar este razonamiento con un algoritmo que, por cada posible
etiqueta, explícitamente actualiza el modelo para tratar de explicar esa etiqueta para la consulta
y combina los diferentes modelos para obtener predicciones bien calibradas
para los insumos fuera de distribución. En esta entrada del blog, motivaremos y
presentar
amortizada condicional normalizada máxima probabilidad
(ACNML), una instanciación práctica de esta idea que permite una fiable
estimación de la incertidumbre con redes neuronales profundas.

Nuestro método extiende una estrategia de predicción desde la mínima longitud de descripción
(MDL) literatura conocida como probabilidad máxima condicional normalizada (CNML),
^{que ha sido estudiado por sus propiedades teóricas, pero es computacional
intratable para todos, excepto para los problemas más simples. Primero revisaremos la CNML y
discutir cómo sus predicciones pueden llevar a estimaciones conservadoras de incertidumbre. Nosotros
describirá nuestro método, que permite una aplicación práctica del CNML
para obtener estimaciones de incertidumbre para las redes neuronales profundas.}

La distribución CNML se deriva de la consecución de una noción de optimización mínima,
donde definimos una noción de arrepentimiento para cada etiqueta y elegimos la distribución
que minimiza el peor caso de arrepentimiento sobre las etiquetas. Dado un conjunto de entrenamiento
$D_{{\N- tren}$, una entrada de consulta $x$, y un conjunto de modelos potenciales $N- Theta$, nosotros
definir el arrepentimiento de cada etiqueta como la diferencia entre el negativo
la pérdida de probabilidad de registro para nuestra distribución y la pérdida según el modelo que mejor
encaja el conjunto de datos de entrenamiento junto con el punto de consulta y la etiqueta.

Intuitivamente, minimizar el peor caso de arrepentimiento sobre las etiquetas, entonces asegura nuestra
La distribución predictiva es conservadora, ya que no puede asignar probabilidades bajas
a cualquier etiqueta que parezca consistente con nuestros datos de entrenamiento, donde la consistencia
está determinado por la clase de modelo.

La distribución mínima óptima dada una entrada particular $x$ y un conjunto de entrenamiento
D$ matemático puede ser calculado explícitamente de la siguiente manera:

1. Por cada etiqueta $y$, añadimos $(x,y)$ a nuestro set de entrenamiento y calculamos el
   nuevos parámetros óptimos para este conjunto de entrenamiento modificado.

2. Usa $Nque N-que N-la iota para asignar la probabilidad de esa etiqueta.

3. Dado que estas probabilidades ahora se sumarán a un número mayor que 1, nosotros
   normalizar para obtener una distribución válida sobre las etiquetas.

El CNML tiene la interesante propiedad de que optimiza explícitamente el modelo para
hacer predicciones sobre la entrada de la consulta, lo que puede conducir a una más razonable
predicciones que simplemente extrapolar usando un modelo obtenido sólo de la
set de entrenamiento. También puede llevar a predicciones más conservadoras sobre
de los insumos fuera de la distribución, ya que sería más fácil ajustar diferentes etiquetas
para los puntos fuera de distribución sin afectar el rendimiento en el entrenamiento
…y el juego.

Ilustramos el CNML con un ejemplo de regresión logística bidimensional. Comparamos
mapas de calor de las probabilidades del CNML con el clasificador de máxima probabilidad para
ilustran cómo el CNML proporciona estimaciones conservadoras de incertidumbre en puntos alejados
de los datos. Con esta clase de modelo, el CNML expresa la incertidumbre y asigna una
distribución uniforme a cualquier punto de consulta donde el conjunto de datos permanezca linealmente
separable (lo que significa que existe un límite de decisión lineal que podría correctamente
clasificar todos los puntos de datos) independientemente de la etiqueta asignada para la consulta
punto.

Ilustramos cómo el CNML calcula estas probabilidades ilustrando la base
las predicciones del clasificador bajo los parámetros que el texto de la
…y también que el set de entrenamiento MLE), así como…
los parámetros calculados por el CNML después de asignar el
etiqueta 0 y 1, respectivamente, a un punto de consulta.

Primero consideramos un punto de consulta fuera de la distribución, lejos de cualquiera de los
de entrenamiento (se muestra en rosa en la parte inferior de la imagen de la izquierda). En el
En la imagen de la izquierda, vemos el límite de la decisión original por $Nque
El texto clasifica con confianza el punto de consulta como clase 0. En
En el medio, vemos el límite de decisión de lo que es similar…
clasifica el punto de consulta como clase 0. Sin embargo, vemos en la imagen de la derecha
…que es capaz de clasificar con confianza el punto de consulta como clase 1.
Ya que eso predice con confianza la clase 0 para el punto de consulta y…
que predice con confianza la clase 1, la CNML normaliza las dos
predicciones para asignar una probabilidad aproximadamente igual a cualquiera de las dos etiquetas.

Figura 3: El punto de consulta se muestra en rosa. Tanto el texto como el
que clasifican el punto de consulta como clase 0, pero que es
capaz de clasificarlo como clase 1.

Por otra parte, para un punto de consulta de distribución (de nuevo en rosa) en
en medio de las entradas de entrenamiento de clase 0, ningún clasificador lineal puede caber en una etiqueta
de 1 al punto de consulta, mientras que todavía se ajusta con precisión el resto de la formación
por lo que la distribución CNML todavía predice con confianza la clase 0 en esta consulta
punto.

Figura 4: Punto de consulta mostrado en rosa. Todos los parámetros están obligados a clasificar el
punto de consulta como clase 0 ya que está en medio del entrenamiento de la clase 0
puntos.

Control del conservadurismo mediante la regularización

Vemos en la figura 2 que las probabilidades del CNML son uniformes en la mayoría de las entradas
el espacio, que podría decirse que es demasiado conservador. En este caso, la clase modelo está en
algún sentido demasiado expresivo, como predictores lineales con grandes coeficientes que
puede asignar probabilidades arbitrariamente altas a cada etiqueta siempre y cuando los datos
permanece linealmente separable. Este problema se agrava con aún más
clases de modelos expresivos como las redes neuronales profundas, que potencialmente pueden encajar
etiquetas arbitrarias. Con el fin de que el CNML proporcione predicciones más útiles, podríamos
necesidad de restringir el conjunto de modelos permitidos para reflejar mejor nuestra noción de
modelos razonables.

Para lograr esto, generalizamos el CNML para incorporar la regularización a través de un
plazo previo, lo que da lugar a una
máximo normalizado a posteriori
(CNMAP) en su lugar. En lugar de computar la máxima probabilidad
parámetros para el conjunto de datos de entrenamiento y la nueva entrada y etiqueta, calculamos
soluciones máximas a posteriori (MAP) en su lugar, con el término anterior $p(theta)$
sirviendo como un regularizador para limitar la complejidad del modelo seleccionado.

Volviendo al ejemplo de la regresión logística, añadimos diferentes niveles de L2
regularización a los parámetros (correspondientes a los antecedentes gausianos) y trazar
Probabilidades de CNMAP en la figura 3 abajo. A medida que aumenta la regularización, la CNML
se vuelve menos conservador, con las probabilidades asignadas en transición mucho
más suavemente a medida que uno se aleja de los puntos de entrenamiento.

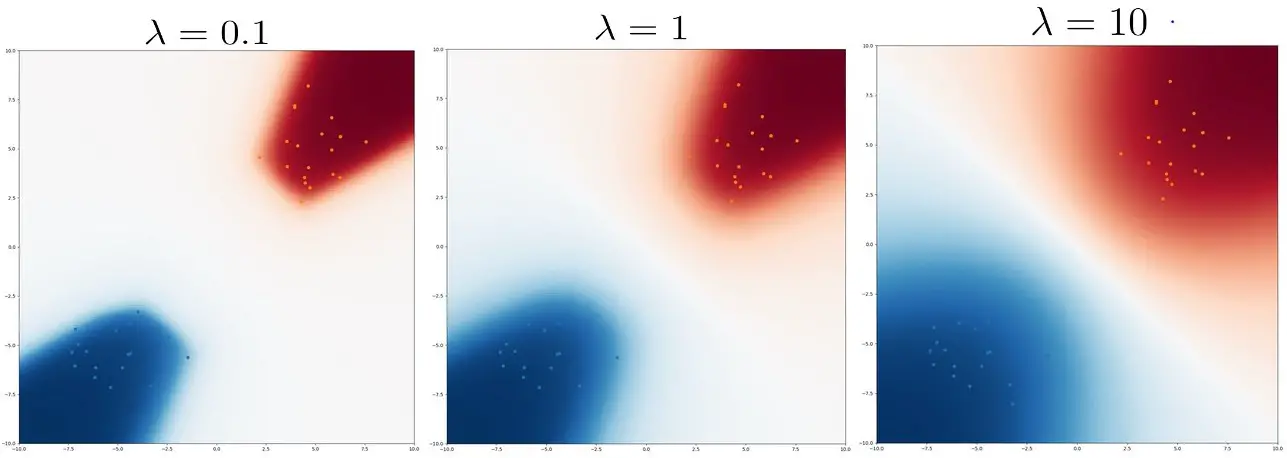
Figura 5: Mapas de calor de las probabilidades de la CNMAP bajo cantidades variables de
regularización $lambda ~ – w ~ – 2^2$. El aumento de la regularización lleva a menos
predicciones conservadoras.

Intratabilidad computacional

Aunque vemos que el CNML es capaz de proporcionar predicciones conservadoras para la OOD
de entrada, el cálculo de las predicciones CNML requiere el reentrenamiento del modelo usando la
todo el conjunto de entrenamiento varias veces para cada entrada de pruebaque puede ser muy
…y es muy costoso. Mientras que computar explícitamente las distribuciones CNML fue
factible en nuestro ejemplo de regresión logística con pequeños conjuntos de datos, sería
computacionalmente intratable para computar el CNML ingenuamente con conjuntos de datos que consisten en
miles de imágenes y usando redes neuronales convolucionales profundas, como reentrenamiento
el modelo sólo una vez ya podría llevar muchas horas. Incluso inicializar desde el
solución al conjunto de entrenamiento y la puesta a punto para varias épocas después de añadir el
la entrada de la consulta y la etiqueta todavía podría tomar varios minutos por entrada, haciendo que
no es práctico para usar con redes neuronales profundas y grandes conjuntos de datos.

Ya que computar exactamente las distribuciones CNML o CNMAP es computacional
no es factible en entornos de aprendizaje profundo debido a la necesidad de optimizar a gran escala
de datos para cada nueva entrada y etiqueta, necesitamos una aproximación trazable. En
nuestro método, amortizada condicional normalizada máxima probabilidad (ACNML), nosotros
utilizan aproximadamente los posteriores bayesianos para capturar la información necesaria sobre
los datos de entrenamiento para computar eficientemente las soluciones MAP/MLE para
cada punto de datos. ACNML amortiza los costos de la optimización repetida sobre la
entrenamiento establecido por el primer cálculo de un posterior bayesiano aproximado, que sirve
como una aproximación compacta a las pérdidas de entrenamiento.

CNMAP y Posteriores Bayesianos

Observamos que el principal cuello de botella computacional es la necesidad de optimizar sobre la
todo el conjunto de entrenamiento para cada punto de consulta. Para evitar este problema, nosotros
muestran primero una relación entre los parámetros MAP necesarios en la CNMAP y
Densidades posteriores bayesianas:

En lugar de calcular los parámetros óptimos para el nuevo punto de consulta y el
podemos reformular la CNMAP para optimizar el punto de consulta…
y una densidad posterior. Con un anterior uniforme (equivalente a no tener
regularizador), podemos recuperar los parámetros de máxima probabilidad para realizar el CNML
si lo desea.

El ACNML ahora utiliza una inferencia bayesiana aproximada para reemplazar la exacta
densidad posterior con una densidad manejable $q(theta)$. Como muchos métodos han
se ha propuesto para aproximarse a la inferencia bayesiana en el aprendizaje profundo, podemos
simplemente utilizar cualquier posterior aproximado que proporcione densidades trazables para
ACNML, aunque nos centramos en los posteriores aproximados de Gauss por simplicidad y
eficiencia computacional. Después de calcular el posterior aproximado una vez durante
el procedimiento de optimización de tiempo de prueba se hace mucho más simple, ya que sólo
necesidad de optimizar sobre nuestro posterior aproximado en lugar del conjunto de entrenamiento.
Cuando instanciamos el ACNML e iniciamos desde la solución MAP, encontramos que
típicamente toma sólo un puñado de actualizaciones de gradientes para calcular nuevos (aproximados)
parámetros óptimos para cada etiqueta, lo que resulta en una inferencia de tiempo de prueba mucho más rápida
que una ingenua instanciación de CNML que afina las melodías usando todo el conjunto de entrenamiento.

En nuestro documento, analizamos la
error de aproximación incurrido al utilizar un posterior Gaussiano particular en el lugar
de las probabilidades exactas de los datos de entrenamiento, y muestran que bajo ciertas
supuestos, la aproximación es precisa cuando el conjunto de entrenamiento es grande.

Experimentos

Instanciamos el ACNML con dos aproximaciones posteriores gaussianas diferentes,
SWAG-Diagonal y
KFAC-Laplace
y los modelos de trenes en el conjunto de datos de clasificación de imágenes CIFAR-10. Para evaluar
rendimiento fuera de la distribución, luego evaluamos en el CIFAR-10 Corrupto
que aplican un rango diverso de corrupciones de imágenes comunes en diferentes
intensidades, lo que nos permite ver lo bien que funcionan los métodos bajo diferentes niveles
del cambio de distribución. Comparamos con los métodos que utilizan el método bayesiano
marginación, que promedia las predicciones de diferentes modelos muestreados de
la parte posterior aproximada. Observamos que todos los métodos proveen muy similares
precisión tanto en la distribución como en la no distribución, así que nos centramos en la comparación
estimaciones de incertidumbre.

Primero examinamos las predicciones del ACNML usando diagramas de fiabilidad, que
agregar los puntos de datos de la prueba en cubos basados en la confianza que el modelo
las predicciones son, entonces trazar la confianza media en un cubo contra la
la exactitud real de las predicciones. Estos diagramas muestran la distribución de
predicen las confidencias y pueden captar la eficacia de la confianza de un modelo
refleja la incertidumbre real sobre la predicción.

Como esperábamos de nuestra discusión anterior sobre el CNML, encontramos que el ACNML
da de forma fiable predicciones más conservadoras (menos confiables) que otras
hasta el punto de que sus predicciones son en realidad poco confiado en
el conjunto de pruebas CIFAR10 de distribución interna donde todos los métodos proporcionan una gran precisión
predicciones. Sin embargo, en las tareas del CIFAR10-C fuera de distribución, donde
la precisión del clasificador se degrada, la conservadurismo del ACNML proporciona mucho más
estimaciones de confianza fiables, mientras que otros métodos tienden a ser severos
demasiado confiado.

Figura 8: Comparaciones ECE: Comparamos instantes de ACNML con dos
diferentes aproximaciones posteriores contra sus homólogos bayesianos.

Medimos cuantitativamente la calibración usando el
Error de calibración esperado,
que utiliza los mismos cubos que los diagramas de fiabilidad y
calcula el error de calibración promedio (diferencia absoluta entre el promedio
confianza y precisión dentro del cubo) sobre todos los cubos. Vemos que el ACNML
Las instancias proporcionan una calibración mucho mejor que sus homólogos bayesianos
y la línea de base determinante a medida que las intensidades de la corrupción aumentan y la
Los datos se vuelven más difíciles de distribuir.

En este post, discutimos cómo podemos obtener estimaciones de incertidumbre fiables sobre
fuera de la distribución de datos mediante la optimización explícita de los datos que deseamos hacer
en lugar de confiar en modelos entrenados para extrapolar de la
datos de entrenamiento. Luego demostramos que esto puede hacerse concretamente con el CNML
estrategia de predicción, un esquema que ha sido estudiado teóricamente pero que es
computacionalmente intratable de aplicar en la práctica. Finalmente presentamos nuestro
método, ACNML, una aproximación práctica al CNML que permite una fiable
estimación de la incertidumbre con redes neuronales profundas. Esperamos que esta línea de
ayudará a permitir una mayor aplicación del aprendizaje de la máquina a gran escala
sistemas, especialmente en ámbitos críticos para la seguridad, donde la estimación de la incertidumbre es
una necesidad.

Agradecemos a Sergey Levine y Dibya Ghosh por proporcionarnos valiosos comentarios en este post.

Este post está basado en el siguiente documento: