
Última actualización el 29 de noviembre de 2022
La regresión lineal es una técnica simple pero poderosa para predecir los valores de las variables en función de otras variables. A menudo se utiliza para modelar relaciones entre dos o más variables continuas, como la relación entre ingresos y edad, o la relación entre peso y altura. Del mismo modo, la regresión lineal se puede utilizar para predecir resultados continuos, como el precio o la demanda de cantidad, en función de otras variables que se sabe que influyen en estos resultados.
Para entrenar un modelo de regresión lineal, necesitamos definir una función de costo y un optimizador. La función de costo se usa para medir qué tan bien se ajusta nuestro modelo a los datos, mientras que el optimizador decide en qué dirección moverse para mejorar este ajuste.
Mientras que en el tutorial anterior aprendió cómo podemos hacer predicciones simples con solo un paso hacia adelante de regresión lineal, aquí entrenará un modelo de regresión lineal y actualizará sus parámetros de aprendizaje usando PyTorch. En particular, aprenderás:
- Cómo puede construir un modelo de regresión lineal simple desde cero en PyTorch.
- Cómo puede aplicar un modelo de regresión lineal simple en un conjunto de datos.
- Cómo se puede entrenar un modelo de regresión lineal simple en un solo parámetro aprendible.
- Cómo se puede entrenar un modelo de regresión lineal simple en dos parámetros que se pueden aprender.
Entonces empecemos.
Entrenamiento de un modelo de regresión lineal en PyTorch.
Imagen de Ryan Tasto. Algunos derechos reservados.
Visión general
Este tutorial consta de cuatro partes; están
- Preparación de datos
- Construcción del modelo y función de pérdida
- Entrenamiento del modelo para un solo parámetro
- Entrenamiento del modelo para dos parámetros
Preparación de datos
Importemos algunas bibliotecas que usaremos en este tutorial y hagamos algunos datos para nuestros experimentos.
import torch
import numpy as np
import matplotlib.pyplot as plt
Usaremos datos sintéticos para entrenar el modelo de regresión lineal. Inicializaremos una variable X con valores de $-5$ a $5$ y cree una función lineal que tenga una pendiente de $-5$. Tenga en cuenta que esta función será estimada por nuestro modelo entrenado más adelante.
…
# Creating a function f(X) with a slope of -5
X = torch.arange(-5, 5, 0.1).view(-1, 1)
func = -5 * X
Además, veremos cómo se ven nuestros datos en un diagrama de líneas, usando matplotlib.
…
# Plot the line in red with grids
plt.plot(X.numpy(), func.numpy(), ‘r’, label=»func»)
plt.xlabel(‘x’)
plt.ylabel(‘y’)
plt.legend()
plt.grid(‘True’, color=»y»)
plt.show()
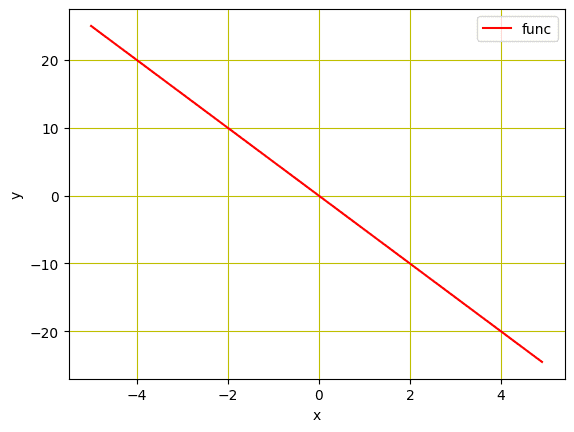
Gráfico de la función lineal
Como necesitamos simular los datos reales que acabamos de crear, agreguemos algo de ruido gaussiano para crear datos con ruido del mismo tamaño que $X$, manteniendo el valor de la desviación estándar en 0,4. Esto se hará usando torch.randn(X.size()).
…
# Adding Gaussian noise to the function f(X) and saving it in Y
Y = func + 0.4 * torch.randn(X.size())
Ahora, visualicemos estos puntos de datos usando las siguientes líneas de código.
# Plot and visualizing the data points in blue
plt.plot(X.numpy(), Y.numpy(), ‘b+’, label=»Y»)
plt.plot(X.numpy(), func.numpy(), ‘r’, label=»func»)
plt.xlabel(‘x’)
plt.ylabel(‘y’)
plt.legend()
plt.grid(‘True’, color=»y»)
plt.show()
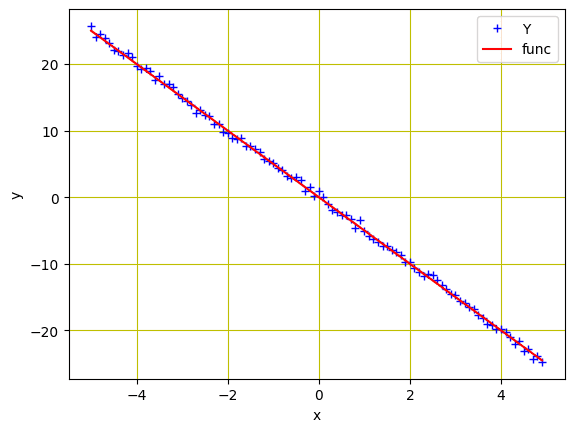
Puntos de datos y la función lineal
Poniendo todo junto, el siguiente es el código completo.
import torch
import numpy as np
import matplotlib.pyplot as plt
# Creating a function f(X) with a slope of -5
X = torch.arange(-5, 5, 0.1).view(-1, 1)
func = -5 * X
# Adding Gaussian noise to the function f(X) and saving it in Y
Y = func + 0.4 * torch.randn(X.size())
# Plot and visualizing the data points in blue
plt.plot(X.numpy(), Y.numpy(), ‘b+’, label=»Y»)
plt.plot(X.numpy(), func.numpy(), ‘r’, label=»func»)
plt.xlabel(‘x’)
plt.ylabel(‘y’)
plt.legend()
plt.grid(‘True’, color=»y»)
plt.show()
Construcción del modelo y función de pérdida
Creamos los datos para alimentar el modelo, luego construiremos una función directa basada en una ecuación de regresión lineal simple. Tenga en cuenta que construiremos el modelo para entrenar solo un único parámetro ($w$) aquí. Más adelante, en la sección Sext del tutorial, agregaremos el sesgo y entrenaremos el modelo para dos parámetros ($w$ y $b$). La función para el pase hacia adelante del modelo se define de la siguiente manera:
# defining the function for forward pass for prediction
def forward(x):
return w * x
En los pasos de entrenamiento, necesitaremos un criterio para medir la pérdida entre los puntos de datos originales y predichos. Esta información es crucial para las operaciones de optimización del descenso de gradiente del modelo y se actualiza después de cada iteración para calcular los gradientes y minimizar la pérdida. Por lo general, la regresión lineal se usa para datos continuos donde el error cuadrático medio (MSE) calcula efectivamente la pérdida del modelo. Por lo tanto, la métrica MSE es la función de criterio que usamos aquí.
# evaluating data points with Mean Square Error.
def criterion(y_pred, y):
return torch.mean((y_pred – y) ** 2)
Entrenamiento del modelo para un solo parámetro
Con todos estos preparativos, estamos listos para el entrenamiento de modelos. Primero, el parámetro $w$ debe inicializarse aleatoriamente, por ejemplo, al valor $-10$.
w = torch.tensor(-10.0, requires_grad=True)
A continuación, definiremos la tasa de aprendizaje o el tamaño del paso, una lista vacía para almacenar la pérdida después de cada iteración y la cantidad de iteraciones para las que queremos que se entrene nuestro modelo. Si bien el tamaño del paso se establece en 0,1, entrenamos el modelo para 20 iteraciones por épocas.
step_size = 0.1
loss_list = []
iter = 20
Cuando se ejecutan las siguientes líneas de código, el forward() La función toma una entrada y genera una predicción. los criterian() función calcula la pérdida y la almacena en loss variable. Con base en la pérdida del modelo, la backward() método calcula los gradientes y w.data almacena los parámetros actualizados.
for i in range (iter):
# making predictions with forward pass
Y_pred = forward(X)
# calculating the loss between original and predicted data points
loss = criterion(Y_pred, Y)
# storing the calculated loss in a list
loss_list.append(loss.item())
# backward pass for computing the gradients of the loss w.r.t to learnable parameters
loss.backward()
# updateing the parameters after each iteration
w.data = w.data – step_size * w.grad.data
# zeroing gradients after each iteration
w.grad.data.zero_()
# priting the values for understanding
print(‘{},t{},t{}’.format(i, loss.item(), w.item()))
El resultado del entrenamiento del modelo se imprime como se muestra a continuación. Como puede ver, la pérdida del modelo se reduce después de cada iteración y el parámetro entrenable (que en este caso es $w$) se actualiza.
0, 207.40255737304688, -1.6875505447387695
1, 92.3563003540039, -7.231954097747803
2, 41.173553466796875, -3.5338361263275146
3, 18.402894973754883, -6.000481128692627
4, 8.272472381591797, -4.355228900909424
5, 3.7655599117279053, -5.452612400054932
6, 1.7604843378067017, -4.7206573486328125
7, 0.8684477210044861, -5.208871364593506
8, 0.471589595079422, -4.883232593536377
9, 0.2950323224067688, -5.100433826446533
10, 0.21648380160331726, -4.955560684204102
11, 0.1815381944179535, -5.052190780639648
12, 0.16599132120609283, -4.987738609313965
13, 0.15907476842403412, -5.030728340148926
14, 0.15599775314331055, -5.002054214477539
15, 0.15462875366210938, -5.021179676055908
16, 0.15401971340179443, -5.008423328399658
17, 0.15374873578548431, -5.016931533813477
18, 0.15362821519374847, -5.011256694793701
19, 0.15357455611228943, -5.015041828155518
También visualicemos a través de la gráfica para ver cómo se reduce la pérdida.
# Plotting the loss after each iteration
plt.plot(loss_list, ‘r’)
plt.tight_layout()
plt.grid(‘True’, color=»y»)
plt.xlabel(«Epochs/Iterations»)
plt.ylabel(«Loss»)
plt.show()
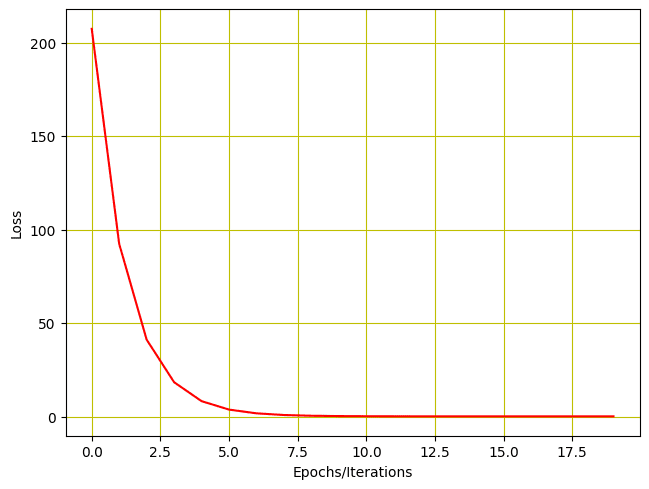
Pérdida de entrenamiento vs épocas
Poniendo todo junto, el siguiente es el código completo:
import torch
import numpy as np
import matplotlib.pyplot as plt
X = torch.arange(-5, 5, 0.1).view(-1, 1)
func = -5 * X
Y = func + 0.4 * torch.randn(X.size())
# defining the function for forward pass for prediction
def forward(x):
return w * x
# evaluating data points with Mean Square Error
def criterion(y_pred, y):
return torch.mean((y_pred – y) ** 2)
w = torch.tensor(-10.0, requires_grad=True)
step_size = 0.1
loss_list = []
iter = 20
for i in range (iter):
# making predictions with forward pass
Y_pred = forward(X)
# calculating the loss between original and predicted data points
loss = criterion(Y_pred, Y)
# storing the calculated loss in a list
loss_list.append(loss.item())
# backward pass for computing the gradients of the loss w.r.t to learnable parameters
loss.backward()
# updateing the parameters after each iteration
w.data = w.data – step_size * w.grad.data
# zeroing gradients after each iteration
w.grad.data.zero_()
# priting the values for understanding
print(‘{},t{},t{}’.format(i, loss.item(), w.item()))
# Plotting the loss after each iteration
plt.plot(loss_list, ‘r’)
plt.tight_layout()
plt.grid(‘True’, color=»y»)
plt.xlabel(«Epochs/Iterations»)
plt.ylabel(«Loss»)
plt.show()
Entrenamiento del modelo para dos parámetros
Agreguemos también bias $b$ a nuestro modelo y entrenémoslo para dos parámetros. Primero necesitamos cambiar la función de reenvío de la siguiente manera.
# defining the function for forward pass for prediction
def forward(x):
return w * x + b
Como tenemos dos parámetros $w$ y $b$, necesitamos inicializar ambos con algunos valores aleatorios, como se muestra a continuación.
w = torch.tensor(-10.0, requires_grad = True)
b = torch.tensor(-20.0, requires_grad = True)
Si bien el resto del código para el entrenamiento seguirá siendo el mismo que antes, solo tendremos que hacer algunos cambios para dos parámetros que se pueden aprender.
Manteniendo la tasa de aprendizaje en 0.1, entrenemos nuestro modelo para dos parámetros durante 20 iteraciones/épocas.
step_size = 0.1
loss_list = []
iter = 20
for i in range (iter):
# making predictions with forward pass
Y_pred = forward(X)
# calculating the loss between original and predicted data points
loss = criterion(Y_pred, Y)
# storing the calculated loss in a list
loss_list.append(loss.item())
# backward pass for computing the gradients of the loss w.r.t to learnable parameters
loss.backward()
# updateing the parameters after each iteration
w.data = w.data – step_size * w.grad.data
b.data = b.data – step_size * b.grad.data
# zeroing gradients after each iteration
w.grad.data.zero_()
b.grad.data.zero_()
# priting the values for understanding
print(‘{}, t{}, t{}, t{}’.format(i, loss.item(), w.item(), b.item()))
Esto es lo que obtenemos para la salida.
0, 598.0744018554688, -1.8875503540039062, -16.046640396118164
1, 344.6290283203125, -7.2590203285217285, -12.802828788757324
2, 203.6309051513672, -3.6438119411468506, -10.261493682861328
3, 122.82559204101562, -6.029742240905762, -8.19227409362793
4, 75.30597686767578, -4.4176344871521, -6.560757637023926
5, 46.759193420410156, -5.476595401763916, -5.2394232749938965
6, 29.318675994873047, -4.757054805755615, -4.19294548034668
7, 18.525297164916992, -5.2265238761901855, -3.3485677242279053
8, 11.781207084655762, -4.90494441986084, -2.677760124206543
9, 7.537606239318848, -5.112729549407959, -2.1378984451293945
10, 4.853880405426025, -4.968738555908203, -1.7080869674682617
11, 3.1505300998687744, -5.060482025146484, -1.3627978563308716
12, 2.0666630268096924, -4.99583625793457, -1.0874838829040527
13, 1.3757448196411133, -5.0362019538879395, -0.8665863275527954
14, 0.9347621202468872, -5.007069110870361, -0.6902718544006348
15, 0.6530535817146301, -5.024737358093262, -0.5489290356636047
16, 0.4729837477207184, -5.011539459228516, -0.43603143095970154
17, 0.3578317165374756, -5.0192131996154785, -0.34558138251304626
18, 0.28417202830314636, -5.013190746307373, -0.27329811453819275
19, 0.23704445362091064, -5.01648473739624, -0.2154112160205841
Del mismo modo, podemos trazar el historial de pérdidas.
# Plotting the loss after each iteration
plt.plot(loss_list, ‘r’)
plt.tight_layout()
plt.grid(‘True’, color=»y»)
plt.xlabel(«Epochs/Iterations»)
plt.ylabel(«Loss»)
plt.show()
Y así es como se ve la trama de la pérdida.
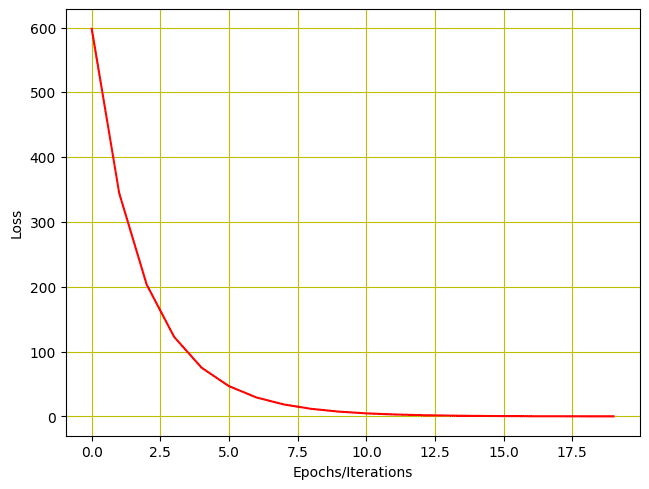
Historial de baja por entrenamiento con dos parámetros
Poniendo todo junto, este es el código completo.
import torch
import numpy as np
import matplotlib.pyplot as plt
X = torch.arange(-5, 5, 0.1).view(-1, 1)
func = -5 * X
Y = func + 0.4 * torch.randn(X.size())
# defining the function for forward pass for prediction
def forward(x):
return w * x + b
# evaluating data points with Mean Square Error.
def criterion(y_pred, y):
return torch.mean((y_pred – y) ** 2)
w = torch.tensor(-10.0, requires_grad=True)
b = torch.tensor(-20.0, requires_grad=True)
step_size = 0.1
loss_list = []
iter = 20
for i in range (iter):
# making predictions with forward pass
Y_pred = forward(X)
# calculating the loss between original and predicted data points
loss = criterion(Y_pred, Y)
# storing the calculated loss in a list
loss_list.append(loss.item())
# backward pass for computing the gradients of the loss w.r.t to learnable parameters
loss.backward()
# updateing the parameters after each iteration
w.data = w.data – step_size * w.grad.data
b.data = b.data – step_size * b.grad.data
# zeroing gradients after each iteration
w.grad.data.zero_()
b.grad.data.zero_()
# priting the values for understanding
print(‘{}, t{}, t{}, t{}’.format(i, loss.item(), w.item(), b.item()))
# Plotting the loss after each iteration
plt.plot(loss_list, ‘r’)
plt.tight_layout()
plt.grid(‘True’, color=»y»)
plt.xlabel(«Epochs/Iterations»)
plt.ylabel(«Loss»)
plt.show()
Resumen
En este tutorial aprendió cómo puede construir y entrenar un modelo de regresión lineal simple en PyTorch. Particularmente, aprendiste.
- Cómo puede construir un modelo de regresión lineal simple desde cero en PyTorch.
- Cómo puede aplicar un modelo de regresión lineal simple en un conjunto de datos.
- Cómo se puede entrenar un modelo de regresión lineal simple en un solo parámetro aprendible.
- Cómo se puede entrenar un modelo de regresión lineal simple en dos parámetros que se pueden aprender.
La publicación Entrenamiento de un modelo de regresión lineal en PyTorch apareció primero en MachineLearningMastery.com.
