Las dos perspectivas más comunes sobre el aprendizaje de refuerzo (RL) son optimización y programación dinámica. Los métodos que calculan los gradientes del objetivo de recompensa esperada no diferenciable, como el truco REINFORCE, suelen agruparse en la perspectiva de la optimización, mientras que los métodos que emplean el TD-learning o el Q-learning son métodos de programación dinámica. Si bien estos métodos han tenido un éxito considerable en los últimos años, su aplicación a nuevos problemas sigue siendo bastante difícil. Por el contrario, el aprendizaje supervisado en profundidad ha tenido mucho éxito y, por lo tanto, podemos preguntarnos: ¿Podemos usar el aprendizaje supervisado para realizar RL?
En esta entrada del blog discutimos un modelo mental para RL, basado en la idea de que RL puede ser visto como un aprendizaje supervisado sobre los «buenos datos». Lo que hace que RL sea un reto es que, a menos que estés haciendo un aprendizaje de imitación, adquirir realmente esos «buenos datos» es bastante difícil. Por lo tanto, RL podría ser vista como una optimización conjunta problema sobre la política y los datos. Visto desde este punto de vista aprendizaje supervisado En perspectiva, muchos algoritmos de RL pueden ser vistos como alternando entre encontrar buenos datos y hacer un aprendizaje supervisado sobre esos datos. Resulta que encontrar «buenos datos» es mucho más fácil en el entorno de tareas múltiples, o en entornos que pueden convertirse en un problema diferente para el que es fácil obtener «buenos datos». De hecho, discutiremos cómo técnicas como el re-etiquetado retrospectivo y la RL inversa pueden ser vistas como una optimización de los datos.
Empezaremos revisando las dos perspectivas comunes de RL, la optimización y la programación dinámica. Luego profundizaremos en una definición formal de la perspectiva de aprendizaje supervisado en RL.
Perspectivas comunes sobre RL
En esta sección, describiremos las dos perspectivas predominantes sobre RL.
Perspectiva de optimización
La perspectiva de optimización considera a RL como un caso especial de optimización de funciones no diferenciables. Recuerda que la recompensa esperada es una función de los parámetros de una póliza:
Esta función es compleja y por lo general indiferenciable y desconocida, ya que depende tanto de las acciones elegidas por la política como de la dinámica del medio ambiente. Aunque podemos estimar el gradiente utilizando el truco del REFUERZO, este gradiente depende de los parámetros de la política y de los datos de la política, que se generan desde el simulador ejecutando la política actual.
Perspectiva de programación dinámica
La perspectiva de la programación dinámica dice que el control óptimo es un problema de elegir la acción correcta en cada paso. En escenarios discretos con dinámicas conocidas, podemos resolver este problema de programación dinámica con exactitud. Por ejemplo, Q-learning estima los valores de acción del estado, $Q(s, a)$ iterando las siguientes actualizaciones:
En espacios continuos o en escenarios con grandes espacios de estado y acción, podemos aproximado programación dinámica mediante la representación de la función Q utilizando un aproximador de funciones (por ejemplo, una red neuronal) y minimizando la diferencia el error TD, que es la diferencia al cuadrado entre el LHS y el RHS en la ecuación anterior:
donde el Objetivo TD $y(s, a) = r(s, a) + gamma N – maximo Q_theta(s’, a’)$. Tenga en cuenta que se trata de una función de pérdida para la función Q, en lugar de la póliza.
Este enfoque permite utilizar cualquier tipo de datos para optimizar la función Q, evitando así la necesidad de disponer de «buenos» datos, pero adolece de importantes problemas de optimización y puede divergir o converger en soluciones deficientes y puede ser difícil de aplicar a nuevos problemas.
Perspectiva de aprendizaje supervisado
Ahora discutimos otro modelo mental para RL. La idea principal es ver a RL como un conjunta problema de optimización sobre la política y la experiencia: queremos encontrar simultáneamente tanto «buenos datos» como una «buena política». Intuitivamente, esperamos que los «buenos» datos (1) obtengan una alta recompensa, (2) exploren suficientemente el medio ambiente, y (3) sean al menos algo representativos de nuestra política. Definimos una buena política como simplemente una política que probablemente produzca buenos datos.
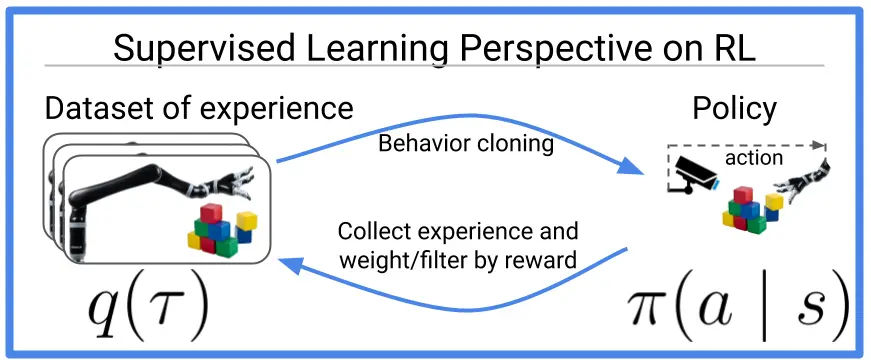
Figura 1: Muchos viejos y nuevos algoritmos de aprendizaje de refuerzo pueden ser vistos como haciendo
clonación de comportamiento (también conocido como aprendizaje supervisado) en datos optimizados. Esta entrada del blog
discute los trabajos recientes que extienden esta idea a la perspectiva multitarea,
donde en realidad se vuelve más fácil optimizar los datos.
Convertir «buenos datos» en una «buena política» es fácil: ¡sólo hay que hacer un aprendizaje supervisado! La dirección inversa, convertir una «buena política» en «buenos datos» es un poco más difícil, y discutiremos algunos enfoques en la siguiente sección. Resulta que en el entorno multitarea o modificando artificialmente la definición del problema ligeramente, convertir una «buena política» en «buenos datos» es sustancialmente más fácil. En la penúltima sección se discutirá cómo el re-etiquetado de objetivos, una definición del problema modificada y la RL inversa extraen «buenos datos» en el entorno multitarea.
Un objetivo de RL que desvincula la política de los datos
Ahora formalizamos la perspectiva de aprendizaje supervisado usando el lente de maximización de expectativas, un lente usado en muchos trabajos anteriores [Dayan 1997, Williams 2007, Peters 2010, Neumann 2011, Levine 2013]. Para simplificar la notación, usaremos $pi_theta(tau)$ como la probabilidad de que la política $pi_theta$ produzca una trayectoria $tau$, y usaremos $q(tau)$ para denotar la distribución de datos que optimizaremos. Considere el registro del objetivo de la recompensa esperada, $log J(theta)$. Dado que la función del log es monótona en aumento, maximizar esto equivale a maximizar la recompensa esperada. Luego aplicamos la desigualdad de Jensen para mover el logaritmo dentro de la expectativa:
Lo útil de este límite inferior es que nos permite optimizar una política utilizando datos muestreados de una política diferente. Este límite inferior hace explícito el hecho de que RL es un problema de optimización conjunta sobre la política y la experiencia. La tabla siguiente compara la perspectiva de aprendizaje supervisado con las perspectivas de optimización y programación dinámica:
| Perspectiva de optimización | Perspectiva de programación dinámica | Perspectiva de aprendizaje supervisado | |
|---|---|---|---|
| ¿Qué estamos optimizando? | política ($pi_theta$) | Q-función ($Q_theta$) | política ($pi_theta$) y datos ($q(tau)$) |
| Pérdida | Pérdida de la madre de alquiler hasta que se haga realidad, que es lo que se hace. |
Error de TD | Límite inferior F(|theta, q)$ |
| Los datos utilizados en la pérdida | recogidas de la política actual | arbitraria | datos optimizados |
Encontrar buenos datos y una buena política corresponde a la optimización del límite inferior, $F(theta, q)$, con respecto a los parámetros de la política y la experiencia. Un enfoque común para maximizar el límite inferior es realizar un ascenso coordinado de sus argumentos, alternando entre la optimización de la distribución de los datos y la política.
Optimizar la política
Cuando se optimiza el límite inferior con respecto a la política, el objetivo es (hasta una constante) exactamente equivalente al aprendizaje supervisado (a.k.a. clonación de comportamiento)!
Esta observación es emocionante porque el aprendizaje supervisado es generalmente mucho más estable que los algoritmos RL. Además, esta observación sugiere que los métodos de RL anteriores que utilizan el aprendizaje supervisado como subrutina[Oh20 18, Ding 2019] podría estar optimizando un límite inferior en la recompensa esperada.
Optimización de la distribución de datos
El objetivo de la distribución de los datos es maximizar la recompensa sin desviarse demasiado de la política actual.
La restricción KL anterior hace que la optimización de la distribución de datos sea conservadora, prefiriendo mantenerse cerca de la política actual a costa de una recompensa ligeramente menor. La optimización de la esperada log recompensa, en lugar de la recompensa esperada, hace que este problema de optimización sea averso al riesgo (la función $log(cdot)$ es una función de utilidad cóncava[^Ingersoll19]).
Hay varias maneras de optimizar la distribución de los datos. Una estrategia sencilla (aunque ineficiente) es recoger la experiencia con una versión ruidosa de la política actual, y mantener el 10% de la experiencia que recibe la mayor recompensa.[^Oh18] Una alternativa es hacer la optimización de la trayectoria, optimizando los estados a lo largo de una sola trayectoria.[Neumann 2011, Levine 2013] Un tercer enfoque es no recoger más datos, sino más bien re ponderar las trayectorias recogidas anteriormente por su recompensa. [Dayan1997] Además, la distribución de los datos $q(tau)$ puede representarse de múltiples maneras – como una distribución discreta no paramétrica sobre trayectorias previamente observadas[Oh 2018]o una distribución factorizada sobre pares de acción de estado individuales [Neumann 2011, Levine 2013] o como un modelo semiparamétrico que amplía la experiencia observada con la experiencia alucinada adicional generada por un modelo paramétrico.[Kumar 2019]
Ver el trabajo previo a través de la lente del aprendizaje supervisado
Un número de algoritmos realizan estos pasos de forma encubierta. Por ejemplo, la regresión ponderada por la recompensa [Williams 2007] y la regresión ponderada por ventajas [Neumann 2009, Peng 2019] combinar los dos pasos haciendo la clonación de comportamiento en datos ponderados por la recompensa. Aprendizaje de autoimitación [Oh 2018] forma la distribución de los datos clasificando las trayectorias observadas según su recompensa y eligiendo una distribución uniforme en la parte superior de la tabla. MPO [Abdolmaleki 2018] construye un conjunto de datos mediante el muestreo de acciones de la política, vuelve a ponderar aquellas acciones que se espera que conduzcan a una alta recompensa (es decir, que tengan una alta recompensa más valor), y luego realiza la clonación de comportamiento en esas acciones re-ponderadas.
Versiones multitarea de la Perspectiva de Aprendizaje Supervisado
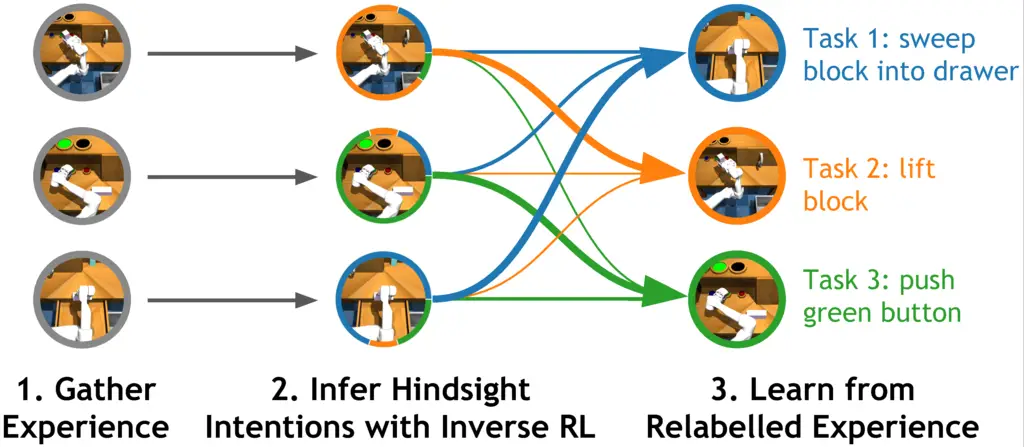
Figura 2: Varios algoritmos recientes de RL multitarea organizan la experiencia
basado en la tarea que cada pieza de experiencia resolvió. Este proceso de post-hoc
está estrechamente relacionada con el re-etiquetado retrospectivo y la RL inversa, y miente
en el núcleo de los recientes algoritmos de RL multitarea que se basan en la supervisión
…aprender.
Varios algoritmos recientes pueden ser vistos como reencarnaciones de esta idea, con un giro. El giro es que encontrar buenos datos se hace mucho más fácil en el entorno multitarea. Estos trabajos típicamente operan directamente en un entorno multitarea o modifican el entorno de una sola tarea para que parezca uno. A medida que aumentamos el número de tareas, toda la experiencia se vuelve óptima para alguna tarea. Ahora vemos tres trabajos recientes a través de esta lente:
Aprendizaje de imitación condicionado a un objetivo:[Savinov 2018, Ghosh 2019, Ding 2019, Lynch 2020] En una tarea de alcance de objetivos, nuestra distribución de datos consiste tanto en los estados y acciones, como en el objetivo intentado. Como el fracaso de un robot para alcanzar un objetivo comandado es, sin embargo, un éxito para alcanzar el objetivo que realmente alcanzó, podemos optimizar la distribución de datos reemplazando los objetivos originalmente comandados por los objetivos realmente alcanzados. Así, el re-etiquetado retrospectivo realizado por el aprendizaje de imitación condicionado por el objetivo [Savinov 2018, Ghosh 2019, Ding 2019, Lynch 2020] y la experiencia retrospectiva se repite [Andrychowicz 2017] puede considerarse como la optimización de una distribución de datos no paramétricos. Además, la imitación condicionada a un objetivo puede verse como una simple realización de aprendizaje supervisado (también conocido como clonación de comportamiento) sobre datos optimizados. Curiosamente, cuando este procedimiento de imitación condicionada por objetivos con re-etiquetado se repite de forma iterativa, se puede demostrar que se trata de un procedimiento convergente para el aprendizaje de políticas desde cero, ¡incluso si no se proporcionan datos expertos en absoluto! [Ghosh 2018] Esto es particularmente prometedor porque nos proporciona esencialmente una técnica para la RL fuera de la política sin requerir explícitamente ningún bootstrapping o aprendizaje de la función de valor, simplificando significativamente el algoritmo y el proceso de ajuste.
Políticas de recompensa condicionadas:[Kumar 2019, Srivastava 2019] Curiosamente, podemos ampliar la comprensión que se ha expuesto anteriormente a la RL de una sola tarea, si podemos ver las trayectorias no expertas recogidas de las políticas no óptimas como una supervisión óptima para alguna familia de tareas. Por supuesto, estas trayectorias sub-óptimas pueden no maximizar la recompensa, pero son óptimas para igualar la recompensa de la trayectoria dada. Así pues, podemos modificar la política para que esté condicionada a un valor deseado de recompensa a largo plazo (es decir, el rendimiento) y seguir una estrategia similar a la del aprendizaje de imitación condicionado por objetivos: ejecutar los despliegues utilizando esta política condicionada por la recompensa ordenando un valor de rendimiento deseado, reetiquetar los valores de rendimiento ordenados a los rendimientos observados, lo que nos proporciona datos optimizados de forma no paramétrica, y por último, ejecutar el aprendizaje supervisado sobre estos datos optimizados. Mostramos [Kumar 2019] que simplemente optimizando los datos de forma no paramétrica mediante sencillos esquemas de reponderación, podemos obtener un método RL que garantiza la convergencia con la política óptima y que es más sencillo que la mayoría de los métodos RL, ya que no requiere estimadores de retorno paramétricos que podrían ser difíciles de ajustar.
Inferencia retrospectiva para la mejora de las políticas:[Eysenbach 2020] Si bien las conexiones entre los algoritmos de alcance de objetivos y la optimización de los conjuntos de datos son claras, hasta hace poco no estaba claro cómo aplicar ideas similares a entornos multitarea más generales, como un conjunto discreto de funciones de recompensa o conjuntos de recompensas definidos por diversas combinaciones (lineales) de términos de bonificación y penalización. Para resolver esta pregunta abierta, comenzamos con la intuición de que la optimización de la distribución de datos corresponde a la respuesta a la siguiente pregunta: «si asumes que tu experiencia fue óptima, ¿qué tareas estabas tratando de resolver?» Intrigantemente, esta es precisamente la pregunta que RL inverso respuestas. Esto sugiere que podemos simplemente usar la RL inversa para reetiquetar los datos en arbitraria Configuración multitarea: La RL inversa proporciona un mecanismo teóricamente conectado a tierra para compartir la experiencia a través de las tareas. Este resultado es emocionante por dos razones:
- Este resultado nos dice cómo aplicar ideas similares de re-etiquetado a entornos multitarea más generales. Nuestros experimentos mostraron que la experiencia de re-etiquetado usando RL inversa acelera el aprendizaje a través de una amplia gama de configuraciones de multitarea, e incluso superó los métodos anteriores de re-etiquetado de objetivos en tareas de alcance de objetivos.
- Resulta que re-etiquetar con el objetivo realmente alcanzado es exactamente equivalente a hacer RL inversa con una cierta función de recompensa escasa. Este resultado nos permite interpretar las técnicas anteriores de re-etiquetado con el objetivo como RL inversa, proporcionando así una base teórica más sólida para estos métodos. En términos más generales, este resultado es emocionante
Direcciones futuras
En este artículo, discutimos cómo RL puede ser visto como la solución de una secuencia de problemas de aprendizaje supervisado estándar pero usando datos optimizados (relaccionados). Este éxito del aprendizaje supervisado profundo durante la última década podría indicar que tales enfoques de RL pueden ser más fáciles de usar en la práctica. Si bien los progresos realizados hasta ahora son prometedores, hay varias cuestiones abiertas. En primer lugar, ¿cuáles podrían ser las otras (mejores) formas de obtener datos optimizados? ¿La reponderación o la recombinación de la experiencia existente induce a un sesgo en el proceso de aprendizaje? ¿Cómo debería explorar el algoritmo RL para obtener mejores datos? Es probable que los métodos y análisis que avanzan en este frente también proporcionen conocimientos para los algoritmos derivados de perspectivas alternativas sobre RL. En segundo lugar, estos métodos podrían proporcionar una forma fácil de trasladar las técnicas prácticas y los análisis teóricos del aprendizaje profundo a RL, que de otro modo son difíciles debido a los objetivos no convexos (por ejemplo, gradientes de política) o al desajuste en la optimización y el objetivo del tiempo de prueba (por ejemplo, el error de Bellman y la devolución de la política). Estamos entusiasmados con varias perspectivas que ofrecen estos métodos: mejores algoritmos prácticos de RL, mejor comprensión de los métodos de RL, etc.
Agradecemos a Allen Zhu, Shreyas Chaudhari, Sergey Levine, y Daniel Seita por sus comentarios sobre este
poste.
Este puesto se basa en los siguientes documentos:
- Ghosh, D., Gupta, A., Fu, J., Reddy, A., Devin, C., Eysenbach, B., y Levine,
S. (2019). Aprendiendo a alcanzar metas a través de un aprendizaje supervisado e iterado
arXiv:1912.06088. - Eysenbach, B., Geng, X., Levine, S., y Salakhutdinov, R. (2020). Reescritura
Historia con RL inverso: Inferencia retrospectiva para la mejora de la política. NeurIPS 2020 (oral). - Kumar, A., Peng, X. B., & Levine, S. (2019). Políticas de recompensa condicionadas.
arXiv:1912.13465.
