Descenso de gradiente es un algoritmo de optimización que sigue el gradiente negativo de una función objetivo para localizar el mínimo de la función.
Un problema con el descenso de gradiente es que puede rebotar alrededor del espacio de búsqueda en problemas de optimización que tienen grandes cantidades de curvatura o gradientes ruidosos, y puede atascarse en puntos planos en el espacio de búsqueda que no tienen gradiente.
Impulso es una extensión del algoritmo de optimización del descenso de gradientes que permite que la búsqueda genere inercia en una dirección en el espacio de búsqueda y supere las oscilaciones de gradientes ruidosos y la costa a través de puntos planos del espacio de búsqueda.
En este tutorial, descubrirá el descenso de gradiente con el algoritmo de impulso.
Después de completar este tutorial, sabrá:
- El descenso de gradiente es un algoritmo de optimización que utiliza el gradiente de la función objetivo para navegar por el espacio de búsqueda.
- El descenso de gradiente se puede acelerar utilizando el impulso de actualizaciones pasadas a la posición de búsqueda.
- Cómo implementar la optimización del descenso de gradientes con impulso y desarrollar una intuición para su comportamiento.
Empecemos.

Descenso de gradiente con impulso desde cero
Foto de Chris Barnes, algunos derechos reservados.
Descripción general del tutorial
Este tutorial se divide en tres partes; son:
- Descenso de gradiente
- Impulso
- Descenso de gradiente con impulso
- Problema de prueba unidimensional
- Optimización del descenso de gradientes
- Visualización de la optimización del descenso de gradientes
- Optimización del descenso de gradientes con impulso
- Visualización de la optimización del descenso de gradientes con Momentum
Descenso de gradiente
El descenso de gradientes es un algoritmo de optimización.
Técnicamente se le conoce como un algoritmo de optimización de primer orden, ya que hace uso explícito de la derivada de primer orden de la función objetivo objetivo.
Los métodos de primer orden se basan en la información del gradiente para ayudar a dirigir la búsqueda de un mínimo …
– Página 69, Algoritmos de optimización, 2019.
La derivada de primer orden, o simplemente la «derivado, ”Es la tasa de cambio o pendiente de la función objetivo en un punto específico, p. para una entrada específica.
Si la función de destino toma múltiples variables de entrada, se la denomina función multivariante y las variables de entrada se pueden considerar como un vector. A su vez, la derivada de una función objetivo multivariante también puede tomarse como un vector y se denomina generalmente «gradiente».
- Degradado: Derivada de primer orden para una función objetivo multivariante.
La derivada o el gradiente apunta en la dirección del ascenso más pronunciado de la función objetivo para una entrada específica.
El descenso de gradiente se refiere a un algoritmo de optimización de minimización que sigue el negativo del gradiente cuesta abajo de la función objetivo para localizar el mínimo de la función.
El algoritmo de descenso de gradiente requiere una función objetivo que se está optimizando y la función derivada para la función objetivo. La función objetivo F() devuelve una puntuación para un conjunto dado de entradas y la función derivada F'() da la derivada de la función objetivo para un conjunto dado de entradas.
El algoritmo de descenso de gradiente requiere un punto de partida (X) en el problema, como un punto seleccionado al azar en el espacio de entrada.
Luego se calcula la derivada y se da un paso en el espacio de entrada que se espera que resulte en un movimiento cuesta abajo en la función objetivo, asumiendo que estamos minimizando la función objetivo.
Un movimiento cuesta abajo se realiza calculando primero qué tan lejos moverse en el espacio de entrada, calculado como el tamaño del paso (llamado alfa o el tasa de aprendizaje) multiplicado por el gradiente. Esto luego se resta del punto actual, asegurando que nos movemos contra el gradiente o hacia abajo de la función de destino.
- x = x – tamaño_paso * f ‘(x)
Cuanto más pronunciada sea la función objetivo en un punto dado, mayor será la magnitud del gradiente y, a su vez, mayor será el paso dado en el espacio de búsqueda. El tamaño del paso realizado se escala mediante un hiperparámetro de tamaño de paso.
- Numero de pie (alfa): Hiperparámetro que controla qué tan lejos moverse en el espacio de búsqueda contra el gradiente en cada iteración del algoritmo, también llamado tasa de aprendizaje.
Si el tamaño del paso es demasiado pequeño, el movimiento en el espacio de búsqueda será pequeño y la búsqueda llevará mucho tiempo. Si el tamaño del paso es demasiado grande, la búsqueda puede rebotar en el espacio de búsqueda y omitir los óptimos.
Ahora que estamos familiarizados con el algoritmo de optimización del descenso de gradientes, echemos un vistazo al impulso.
Impulso
Momentum es una extensión del algoritmo de optimización del descenso de gradientes, a menudo denominado descenso de gradiente con impulso.
Está diseñado para acelerar el proceso de optimización, p. Ej. disminuir el número de evaluaciones de funciones requeridas para alcanzar los óptimos, o para mejorar la capacidad del algoritmo de optimización, p. resultar en un mejor resultado final.
Un problema con el algoritmo de descenso de gradiente es que la progresión de la búsqueda puede rebotar alrededor del espacio de búsqueda según el gradiente. Por ejemplo, la búsqueda puede progresar cuesta abajo hacia los mínimos, pero durante esta progresión, puede moverse en otra dirección, incluso cuesta arriba, dependiendo de la pendiente de puntos específicos (conjuntos de parámetros) encontrados durante la búsqueda.
Esto puede ralentizar el progreso de la búsqueda, especialmente para aquellos problemas de optimización en los que la tendencia o forma más amplia del espacio de búsqueda es más útil que los gradientes específicos en el camino.
Un enfoque para este problema es agregar el historial a la ecuación de actualización de parámetros en función del gradiente encontrado en las actualizaciones anteriores.
Este cambio se basa en la metáfora del impulso de la física donde la aceleración en una dirección se puede acumular a partir de actualizaciones pasadas.
El nombre de momento se deriva de una analogía física, en la que el gradiente negativo es una fuerza que mueve una partícula a través del espacio de parámetros, de acuerdo con las leyes del movimiento de Newton.
– Página 296, Deep Learning, 2016.
Momentum implica agregar un hiperparámetro adicional que controla la cantidad de historial (momentum) para incluir en la ecuación de actualización, es decir, el paso a un nuevo punto en el espacio de búsqueda. El valor del hiperparámetro se define en el rango de 0,0 a 1,0 y, a menudo, tiene un valor cercano a 1,0, como 0,8, 0,9 o 0,99. Un impulso de 0.0 es lo mismo que un descenso de gradiente sin impulso.
Primero, dividamos la ecuación de actualización del descenso del gradiente en dos partes: el cálculo del cambio a la posición y la actualización de la posición anterior a la nueva.
El cambio en los parámetros se calcula como el gradiente para el punto escalado por el tamaño del paso.
- change_x = step_size * f ‘(x)
La nueva posición se calcula simplemente restando el cambio del punto actual
El impulso implica mantener el cambio de posición y utilizarlo en el cálculo posterior del cambio de posición.
Si pensamos en actualizaciones a lo largo del tiempo, entonces la actualización en la iteración actual o en el momento
- change_x
La actualización de la posición se realiza como antes.
- x
El cambio en la posición acumula magnitud y dirección de cambios sobre las iteraciones de la búsqueda, proporcional al tamaño del hiperparámetro de impulso.
Por ejemplo, un gran impulso (por ejemplo, 0,9) significará que la actualización está fuertemente influenciada por la actualización anterior, mientras que un impulso modesto (0,2) significará muy poca influencia.
El algoritmo de impulso acumula un promedio móvil de gradientes pasados que decae exponencialmente y continúa moviéndose en su dirección.
– Página 296, Deep Learning, 2016.
Momentum tiene el efecto de amortiguar el cambio en el gradiente y, a su vez, el tamaño del paso con cada nuevo punto en el espacio de búsqueda.
El impulso puede aumentar la velocidad cuando la superficie de costo es muy no esférica porque amortigua el tamaño de los pasos a lo largo de las direcciones de alta curvatura, lo que produce una mayor tasa de aprendizaje efectivo a lo largo de las direcciones de baja curvatura.
– Página 21, Redes neuronales: trucos del oficio, 2012.
Momentum es más útil en problemas de optimización donde la función objetivo tiene una gran cantidad de curvatura (por ejemplo, cambia mucho), lo que significa que el gradiente puede cambiar mucho en regiones relativamente pequeñas del espacio de búsqueda.
El método de impulso está diseñado para acelerar el aprendizaje, especialmente frente a altas curvaturas, gradientes pequeños pero consistentes o gradientes ruidosos.
– Página 296, Deep Learning, 2016.
También es útil cuando se estima el gradiente, como a partir de una simulación, y puede ser ruidoso, p. Ej. cuando el gradiente tiene una gran varianza.
Por último, el impulso es útil cuando el espacio de búsqueda es plano o casi plano, p. Ej. gradiente cero. El impulso permite que la búsqueda progrese en la misma dirección que antes del punto plano y cruzar la región plana.
Ahora que estamos familiarizados con lo que es el impulso, veamos un ejemplo trabajado.
Descenso de gradiente con impulso
En esta sección, primero implementaremos el algoritmo de optimización del descenso de gradientes, luego lo actualizaremos para usar el impulso y comparar los resultados.
Problema de prueba unidimensional
Primero, definamos una función de optimización.
Usaremos una función unidimensional simple que eleva al cuadrado la entrada y define el rango de entradas válidas de -1.0 a 1.0.
los objetivo() función a continuación implementa esta función.
|
# función objetiva def objetivo(X): regreso X**2.0 |
Luego, podemos muestrear todas las entradas en el rango y calcular el valor de la función objetivo para cada una.
|
... # definir rango para entrada r_min, r_max = –1.0, 1.0 # rango de entrada de muestra uniformemente en incrementos de 0.1 entradas = arange(r_min, r_max+0,1, 0,1) # calcular objetivos resultados = objetivo(entradas) |
Finalmente, podemos crear una gráfica de línea de las entradas (eje x) versus los valores de la función objetivo (eje y) para obtener una intuición de la forma de la función objetivo que buscaremos.
|
... # crear una gráfica de línea de entrada vs resultado pyplot.trama(entradas, resultados) # mostrar la trama pyplot.show() |
El siguiente ejemplo une esto y proporciona un ejemplo de cómo trazar la función de prueba unidimensional.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 dieciséis 17 18 |
# gráfico de función simple de numpy importar arange de matplotlib importar pyplot # función objetiva def objetivo(X): regreso X**2.0 # definir rango para entrada r_min, r_max = –1.0, 1.0 # rango de entrada de muestra uniformemente en incrementos de 0.1 entradas = arange(r_min, r_max+0,1, 0,1) # calcular objetivos resultados = objetivo(entradas) # crear una gráfica de línea de entrada vs resultado pyplot.trama(entradas, resultados) # mostrar la trama pyplot.show() |
La ejecución del ejemplo crea un gráfico de líneas de las entradas de la función (eje x) y la salida calculada de la función (eje y).
Podemos ver la familiar forma de U llamada parábola.
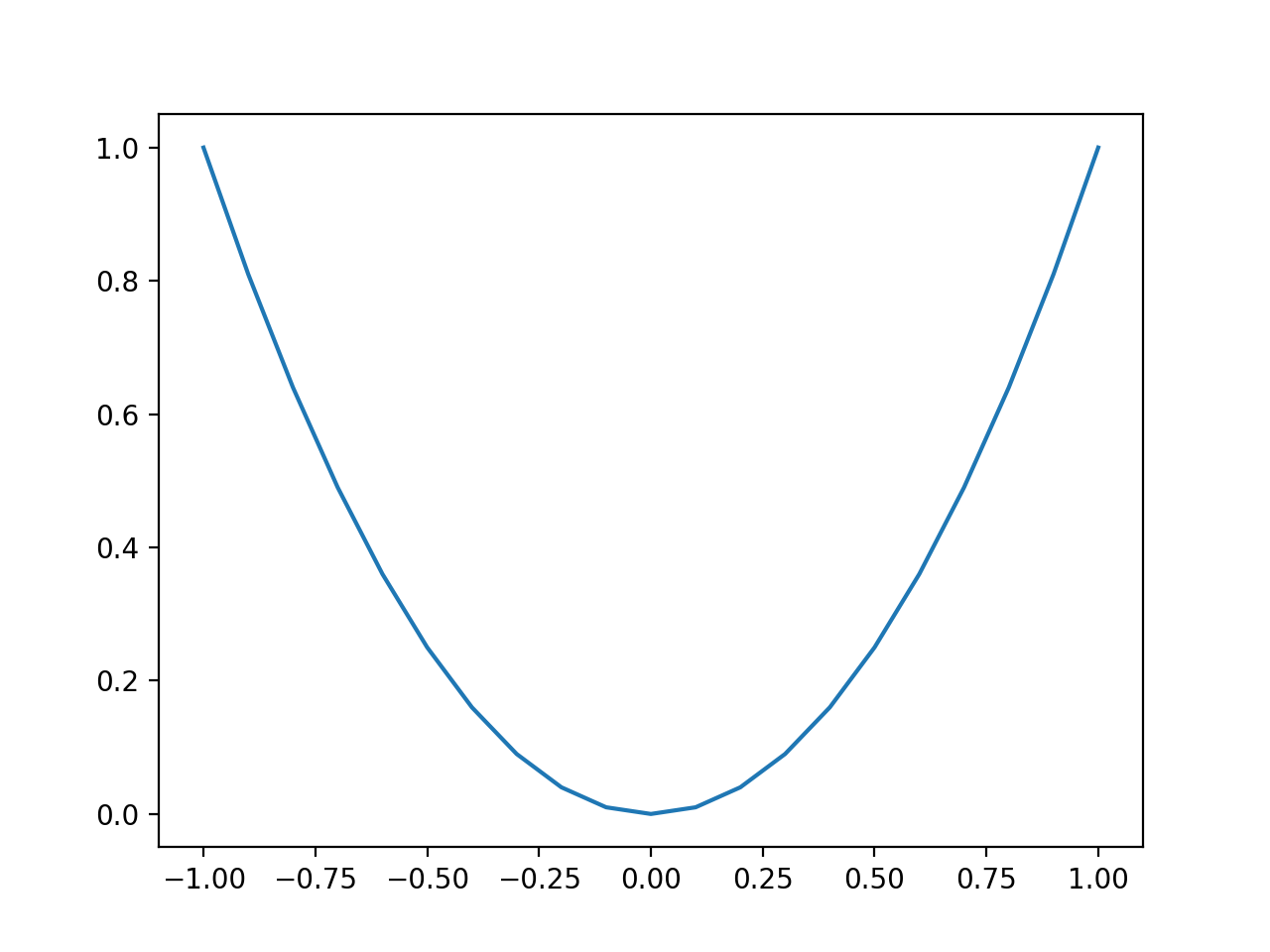
Gráfico de línea de función unidimensional simple
Optimización del descenso de gradientes
A continuación, podemos aplicar el algoritmo de descenso de gradiente al problema.
Primero, necesitamos una función que calcule la derivada de la función objetivo.
La derivada de x ^ 2 es x * 2 y la derivado() La función implementa esto a continuación.
|
# derivada de la función objetivo def derivado(X): regreso X * 2.0 |
Podemos definir una función que implemente el algoritmo de optimización del descenso de gradientes.
El procedimiento implica comenzar con un punto seleccionado al azar en el espacio de búsqueda, luego calcular el gradiente, actualizar la posición en el espacio de búsqueda, evaluar la nueva posición e informar el progreso. Luego, este proceso se repite durante un número fijo de iteraciones. A continuación, la función devuelve el punto final y su evaluación.
La función descenso de gradiente() a continuación implementa esto y toma el nombre de las funciones objetivo y de gradiente, así como los límites de las entradas a la función objetivo, el número de iteraciones y el tamaño del paso, luego devuelve la solución y su evaluación al final de la búsqueda.
|
# algoritmo de descenso de gradiente def descenso de gradiente(objetivo, derivado, límites, nitro, Numero de pie): # generar un punto inicial solución = límites[[:, 0] + rand(len(límites)) * (límites[[:, 1] – límites[[:, 0]) # ejecutar el descenso de gradiente para yo en rango(nitro): # calcular gradiente degradado = derivado(solución) # Da un paso solución = solución – Numero de pie * degradado # evaluar el punto candidato solution_eval = objetivo(solución) # informe de progreso impresión(‘>% d f (% s) =% .5f’ % (yo, solución, solution_eval)) regreso [[solución, solution_eval] |
Luego, podemos definir los límites de la función objetivo, el tamaño del paso y el número de iteraciones del algoritmo.
Usaremos un tamaño de paso de 0.1 y 30 iteraciones, ambas encontradas después de un poco de experimentación.
La semilla para el generador de números pseudoaleatorios es fija para que siempre obtengamos la misma secuencia de números aleatorios y, en este caso, asegura que obtengamos el mismo punto de partida para la búsqueda cada vez que se ejecuta el código (por ejemplo, algo interesante lejos de el optima).
|
... # siembra el generador de números pseudoaleatorios semilla(4) # definir rango para entrada límites = asarray([[[[–1.0, 1.0]]) # definir las iteraciones totales nitro = 30 # definir el tamaño máximo de paso Numero de pie = 0,1 # realizar la búsqueda de descenso de gradiente mejor, Puntuación = descenso de gradiente(objetivo, derivado, límites, nitro, Numero de pie) |
Al unir esto, el ejemplo completo de aplicación de la búsqueda de cuadrícula a nuestra función de prueba unidimensional se enumera a continuación.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 dieciséis 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 |
# ejemplo de descenso de gradiente para una función unidimensional de numpy importar asarray de numpy.aleatorio importar rand de numpy.aleatorio importar semilla # función objetiva def objetivo(X): regreso X**2.0 # derivada de la función objetivo def derivado(X): regreso X * 2.0 # algoritmo de descenso de gradiente def descenso de gradiente(objetivo, derivado, límites, nitro, Numero de pie): # generar un punto inicial solución = límites[[:, 0] + rand(len(límites)) * (límites[[:, 1] – límites[[:, 0]) # ejecutar el descenso de gradiente para yo en rango(nitro): # calcular gradiente degradado = derivado(solución) # Da un paso solución = solución – Numero de pie * degradado # evaluar el punto candidato solution_eval = objetivo(solución) # informe de progreso impresión(‘>% d f (% s) =% .5f’ % (yo, solución, solution_eval)) regreso [[solución, solution_eval] # siembra el generador de números pseudoaleatorios semilla(4) # definir rango para entrada límites = asarray([[[[–1.0, 1.0]]) # definir las iteraciones totales nitro = 30 # definir el tamaño del paso Numero de pie = 0,1 # realizar la búsqueda de descenso de gradiente mejor, Puntuación = descenso de gradiente(objetivo, derivado, límites, nitro, Numero de pie) impresión(‘¡Hecho!’) impresión(‘f (% s) =% f’ % (mejor, Puntuación)) |
La ejecución del ejemplo comienza con un punto aleatorio en el espacio de búsqueda, luego aplica el algoritmo de descenso de gradiente, informando el rendimiento a lo largo del camino.
Nota: Sus resultados pueden variar dada la naturaleza estocástica del algoritmo o procedimiento de evaluación, o las diferencias en la precisión numérica. Considere ejecutar el ejemplo varias veces y compare el resultado promedio.
En este caso, podemos ver que el algoritmo encuentra una buena solución después de aproximadamente 27 iteraciones, con una evaluación de función de aproximadamente 0.0.
Tenga en cuenta que el óptimo para esta función está en f (0.0) = 0.0.
Es de esperar que el descenso de gradiente con impulso acelere el procedimiento de optimización y encuentre una solución evaluada de manera similar en menos iteraciones.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 dieciséis 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 |
> 0 f ([0.74724774]) = 0,55838 > 1 f ([0.59779819]) = 0,35736 > 2 f ([0.47823856]) = 0,22871 > 3 f ([0.38259084]) = 0,14638 > 4 f ([0.30607268]) = 0.09368 > 5 f ([0.24485814]) = 0.05996 > 6 f ([0.19588651]) = 0,03837 > 7 f ([0.15670921]) = 0.02456 > 8 f ([0.12536737]) = 0.01572 > 9 f ([0.10029389]) = 0.01006 > 10 f ([0.08023512]) = 0,00644 > 11 f ([0.06418809]) = 0,00412 > 12 f ([0.05135047]) = 0,00264 > 13 f ([0.04108038]) = 0,00169 > 14 f ([0.0328643]) = 0,00108 > 15 f ([0.02629144]) = 0,00069 > 16 f ([0.02103315]) = 0,00044 > 17 f ([0.01682652]) = 0,00028 > 18 f ([0.01346122]) = 0,00018 > 19 f ([0.01076897]) = 0,00012 > 20 f ([0.00861518]) = 0,00007 > 21 f ([0.00689214]) = 0,00005 > 22 f ([0.00551372]) = 0,00003 > 23 f ([0.00441097]) = 0,00002 > 24 f ([0.00352878]) = 0,00001 > 25 f ([0.00282302]) = 0,00001 > 26 f ([0.00225842]) = 0,00001 > 27 f ([0.00180673]) = 0,00000 > 28 f ([0.00144539]) = 0,00000 > 29 f ([0.00115631]) = 0,00000 ¡Hecho! F([0.00115631]) = 0,000001 |
Visualización de la optimización del descenso de gradientes
A continuación, podemos visualizar el progreso de la búsqueda en un gráfico de la función objetivo.
Primero, podemos actualizar el descenso de gradiente() función para almacenar todas las soluciones y su puntuación encontradas durante la optimización como listas y devolverlas al final de la búsqueda en lugar de la mejor solución encontrada.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 dieciséis 17 18 19 20 |
# algoritmo de descenso de gradiente def descenso de gradiente(objetivo, derivado, límites, nitro, Numero de pie): # rastrear todas las soluciones soluciones, puntuaciones = lista(), lista() # generar un punto inicial solución = límites[[:, 0] + rand(len(límites)) * (límites[[:, 1] – límites[[:, 0]) # ejecutar el descenso de gradiente para yo en rango(nitro): # calcular gradiente degradado = derivado(solución) # Da un paso solución = solución – Numero de pie * degradado # evaluar el punto candidato solution_eval = objetivo(solución) # solución de tienda soluciones.adjuntar(solución) puntuaciones.adjuntar(solution_eval) # informe de progreso impresión(‘>% d f (% s) =% .5f’ % (yo, solución, solution_eval)) regreso [[soluciones, puntuaciones] |
La función se puede llamar y podemos obtener las listas de las soluciones y las puntuaciones encontradas durante la búsqueda.
|
... # realizar la búsqueda de descenso de gradiente soluciones, puntuaciones = descenso de gradiente(objetivo, derivado, límites, nitro, Numero de pie) |
Podemos crear una gráfica lineal de la función objetivo, como antes.
|
... # rango de entrada de muestra uniformemente en incrementos de 0.1 entradas = arange(límites[[0,0], límites[[0,1]+0,1, 0,1) # calcular objetivos resultados = objetivo(entradas) # crear una gráfica de línea de entrada vs resultado pyplot.trama(entradas, resultados) |
Finalmente, podemos trazar cada solución encontrada como un punto rojo y conectar los puntos con una línea para que podamos ver cómo la búsqueda se movió cuesta abajo.
|
... # trazar las soluciones encontradas pyplot.trama(soluciones, puntuaciones, ‘.-‘, color=‘rojo’) |
Al unir todo esto, el ejemplo completo de trazar el resultado de la búsqueda de descenso de gradiente en la función de prueba unidimensional se enumera a continuación.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 dieciséis 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 |
# example of plotting a gradient descent search on a one-dimensional function from numpy import asarray from numpy import arange from numpy.random import rand from numpy.random import seed from matplotlib import pyplot # objective function def objective(X): regreso x**2.0 # derivative of objective function def derivative(X): regreso x * 2.0 # gradient descent algorithm def gradient_descent(objective, derivative, bounds, n_iter, step_size): # track all solutions solutions, scores = list(), list() # generate an initial point solution = bounds[[:, 0] + rand(len(bounds)) * (bounds[[:, 1] – bounds[[:, 0]) # run the gradient descent para yo in range(n_iter): # calculate gradient gradient = derivative(solution) # take a step solution = solution – step_size * gradient # evaluate candidate point solution_eval = objective(solution) # store solution solutions.append(solution) scores.append(solution_eval) # report progress print(‘>%d f(%s) = %.5f’ % (yo, solution, solution_eval)) regreso [[solutions, scores] # seed the pseudo random number generator seed(4) # define range for input bounds = asarray([[[[–1.0, 1.0]]) # define the total iterations n_iter = 30 # define the step size step_size = 0.1 # perform the gradient descent search solutions, scores = gradient_descent(objective, derivative, bounds, n_iter, step_size) # sample input range uniformly at 0.1 increments inputs = arange(bounds[[0,0], bounds[[0,1]+0.1, 0.1) # compute targets results = objective(inputs) # create a line plot of input vs result pyplot.plot(inputs, results) # plot the solutions found pyplot.plot(solutions, scores, ‘.-‘, color=‘red’) # show the plot pyplot.show() |
Running the example performs the gradient descent search on the objective function as before, except in this case, each point found during the search is plotted.
Nota: Your results may vary given the stochastic nature of the algorithm or evaluation procedure, or differences in numerical precision. Consider running the example a few times and compare the average outcome.
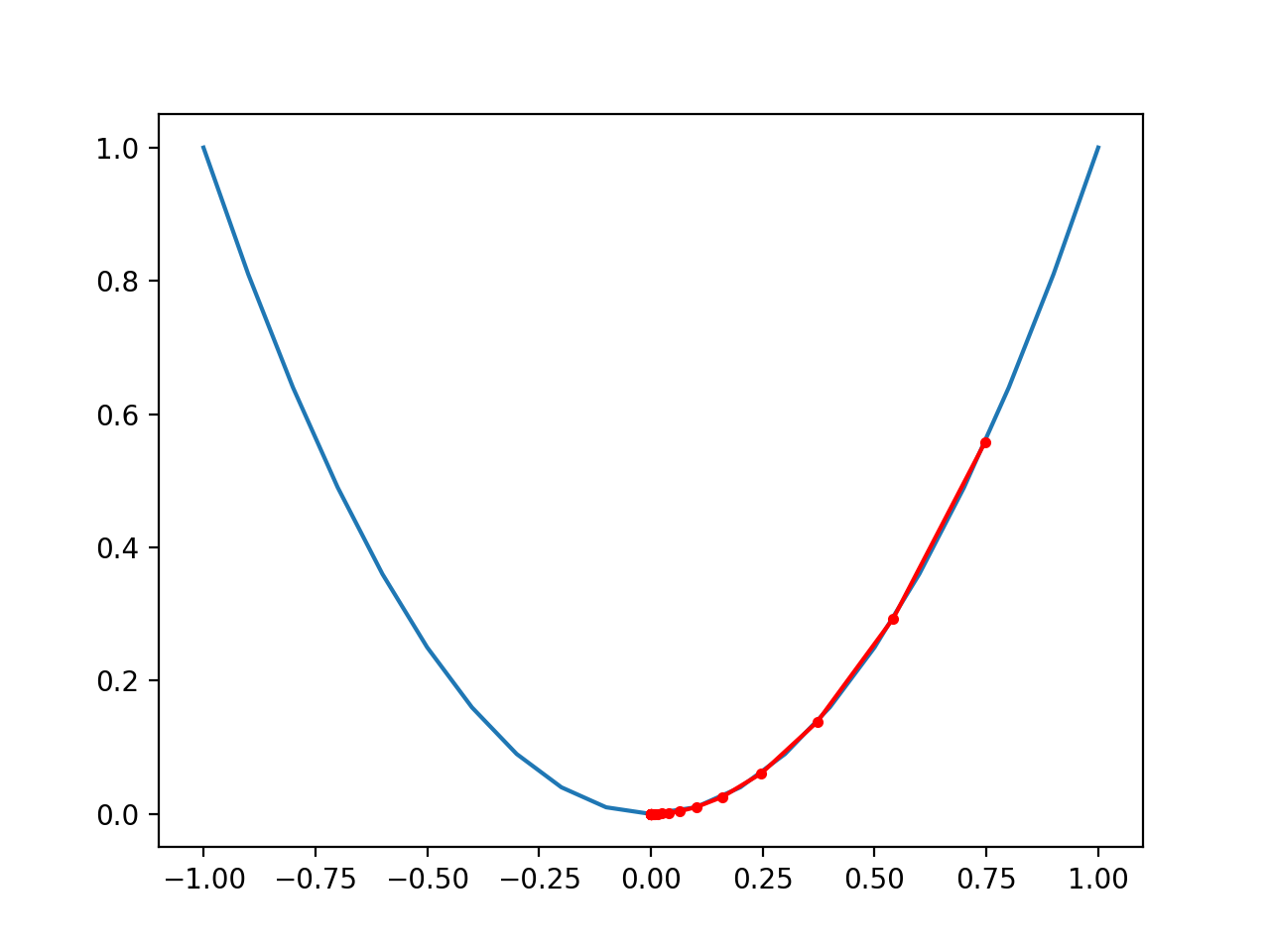
In this case, we can see that the search started more than halfway up the right part of the function and stepped downhill to the bottom of the basin.
We can see that in the parts of the objective function with the larger curve, the derivative (gradient) is larger, and in turn, larger steps are taken. Similarly, the gradient is smaller as we get closer to the optima, and in turn, smaller steps are taken.
This highlights that the step size is used as a scale factor on the magnitude of the gradient (curvature) of the objective function.
Plot of the Progress of Gradient Descent on a One Dimensional Objective Function
Gradient Descent Optimization With Momentum
Next, we can update the gradient descent optimization algorithm to use momentum.
This can be achieved by updating the gradient_descent() function to take a “momentum” argument that defines the amount of momentum used during the search.
The change made to the solution must be remembered from the previous iteration of the loop, with an initial value of 0.0.
|
... # keep track of the change change = 0.0 |
We can then break the update procedure down into first calculating the gradient, then calculating the change to the solution, calculating the position of the new solution, then saving the change for the next iteration.
|
... # calculate gradient gradient = derivative(solution) # calculate update new_change = step_size * gradient + momentum * change # take a step solution = solution – new_change # save the change change = new_change |
The updated version of the gradient_descent() function with these changes is listed below.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 dieciséis 17 18 19 20 21 |
# gradient descent algorithm def gradient_descent(objective, derivative, bounds, n_iter, step_size, momentum): # generate an initial point solution = bounds[[:, 0] + rand(len(bounds)) * (bounds[[:, 1] – bounds[[:, 0]) # keep track of the change change = 0.0 # run the gradient descent para yo in range(n_iter): # calculate gradient gradient = derivative(solution) # calculate update new_change = step_size * gradient + momentum * change # take a step solution = solution – new_change # save the change change = new_change # evaluate candidate point solution_eval = objective(solution) # report progress print(‘>%d f(%s) = %.5f’ % (yo, solution, solution_eval)) regreso [[solution, solution_eval] |
We can then choose a momentum value and pass it to the gradient_descent() function.
After a little trial and error, a momentum value of 0.3 was found to be effective on this problem, given the fixed step size of 0.1.
|
... # define momentum momentum = 0.3 # perform the gradient descent search with momentum best, score = gradient_descent(objective, derivative, bounds, n_iter, step_size, momentum) |
Tying this together, the complete example of gradient descent optimization with momentum is listed below.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 dieciséis 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 |
# example of gradient descent with momentum for a one-dimensional function from numpy import asarray from numpy.random import rand from numpy.random import seed # objective function def objective(X): regreso x**2.0 # derivative of objective function def derivative(X): regreso x * 2.0 # gradient descent algorithm def gradient_descent(objective, derivative, bounds, n_iter, step_size, momentum): # generate an initial point solution = bounds[[:, 0] + rand(len(bounds)) * (bounds[[:, 1] – bounds[[:, 0]) # keep track of the change change = 0.0 # run the gradient descent para yo in range(n_iter): # calculate gradient gradient = derivative(solution) # calculate update new_change = step_size * gradient + momentum * change # take a step solution = solution – new_change # save the change change = new_change # evaluate candidate point solution_eval = objective(solution) # report progress print(‘>%d f(%s) = %.5f’ % (yo, solution, solution_eval)) regreso [[solution, solution_eval] # seed the pseudo random number generator seed(4) # define range for input bounds = asarray([[[[–1.0, 1.0]]) # define the total iterations n_iter = 30 # define the step size step_size = 0.1 # define momentum momentum = 0.3 # perform the gradient descent search with momentum best, score = gradient_descent(objective, derivative, bounds, n_iter, step_size, momentum) print(‘Done!’) print(‘f(%s) = %f’ % (best, score)) |
Running the example starts with a random point in the search space, then applies the gradient descent algorithm with momentum, reporting performance along the way.
Nota: Your results may vary given the stochastic nature of the algorithm or evaluation procedure, or differences in numerical precision. Consider running the example a few times and compare the average outcome.
In this case, we can see that the algorithm finds a good solution after about 13 iterations, with a function evaluation of about 0.0.
As expected, this is faster (fewer iterations) than gradient descent without momentum, using the same starting point and step size that took 27 iterations.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 dieciséis 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 |
>0 f([0.74724774]) = 0.55838 >1 f([0.54175461]) = 0.29350 >2 f([0.37175575]) = 0.13820 >3 f([0.24640494]) = 0.06072 >4 f([0.15951871]) = 0.02545 >5 f([0.1015491]) = 0.01031 >6 f([0.0638484]) = 0.00408 >7 f([0.03976851]) = 0.00158 >8 f([0.02459084]) = 0.00060 >9 f([0.01511937]) = 0.00023 >10 f([0.00925406]) = 0.00009 >11 f([0.00564365]) = 0.00003 >12 f([0.0034318]) = 0.00001 >13 f([0.00208188]) = 0.00000 >14 f([0.00126053]) = 0.00000 >15 f([0.00076202]) = 0.00000 >16 f([0.00046006]) = 0.00000 >17 f([0.00027746]) = 0.00000 >18 f([0.00016719]) = 0.00000 >19 f([0.00010067]) = 0.00000 >20 f([6.05804744e-05]) = 0.00000 >21 f([3.64373635e-05]) = 0.00000 >22 f([2.19069576e-05]) = 0.00000 >23 f([1.31664443e-05]) = 0.00000 >24 f([7.91100141e-06]) = 0.00000 >25 f([4.75216828e-06]) = 0.00000 >26 f([2.85408468e-06]) = 0.00000 >27 f([1.71384267e-06]) = 0.00000 >28 f([1.02900153e-06]) = 0.00000 >29 f([6.17748881e-07]) = 0.00000 Done! f([6.17748881e-07]) = 0.000000 |
Visualization of Gradient Descent Optimization With Momentum
Finally, we can visualize the progress of the gradient descent optimization algorithm with momentum.
The complete example is listed below.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 dieciséis 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 |
# example of plotting gradient descent with momentum for a one-dimensional function from numpy import asarray from numpy import arange from numpy.random import rand from numpy.random import seed from matplotlib import pyplot # objective function def objective(X): regreso x**2.0 # derivative of objective function def derivative(X): regreso x * 2.0 # gradient descent algorithm def gradient_descent(objective, derivative, bounds, n_iter, step_size, momentum): # track all solutions solutions, scores = list(), list() # generate an initial point solution = bounds[[:, 0] + rand(len(bounds)) * (bounds[[:, 1] – bounds[[:, 0]) # keep track of the change change = 0.0 # run the gradient descent para yo in range(n_iter): # calculate gradient gradient = derivative(solution) # calculate update new_change = step_size * gradient + momentum * change # take a step solution = solution – new_change # save the change change = new_change # evaluate candidate point solution_eval = objective(solution) # store solution solutions.append(solution) scores.append(solution_eval) # report progress print(‘>%d f(%s) = %.5f’ % (yo, solution, solution_eval)) regreso [[solutions, scores] # seed the pseudo random number generator seed(4) # define range for input bounds = asarray([[[[–1.0, 1.0]]) # define the total iterations n_iter = 30 # define the step size step_size = 0.1 # define momentum momentum = 0.3 # perform the gradient descent search with momentum solutions, scores = gradient_descent(objective, derivative, bounds, n_iter, step_size, momentum) # sample input range uniformly at 0.1 increments inputs = arange(bounds[[0,0], bounds[[0,1]+0.1, 0.1) # compute targets results = objective(inputs) # create a line plot of input vs result pyplot.plot(inputs, results) # plot the solutions found pyplot.plot(solutions, scores, ‘.-‘, color=‘red’) # show the plot pyplot.show() |
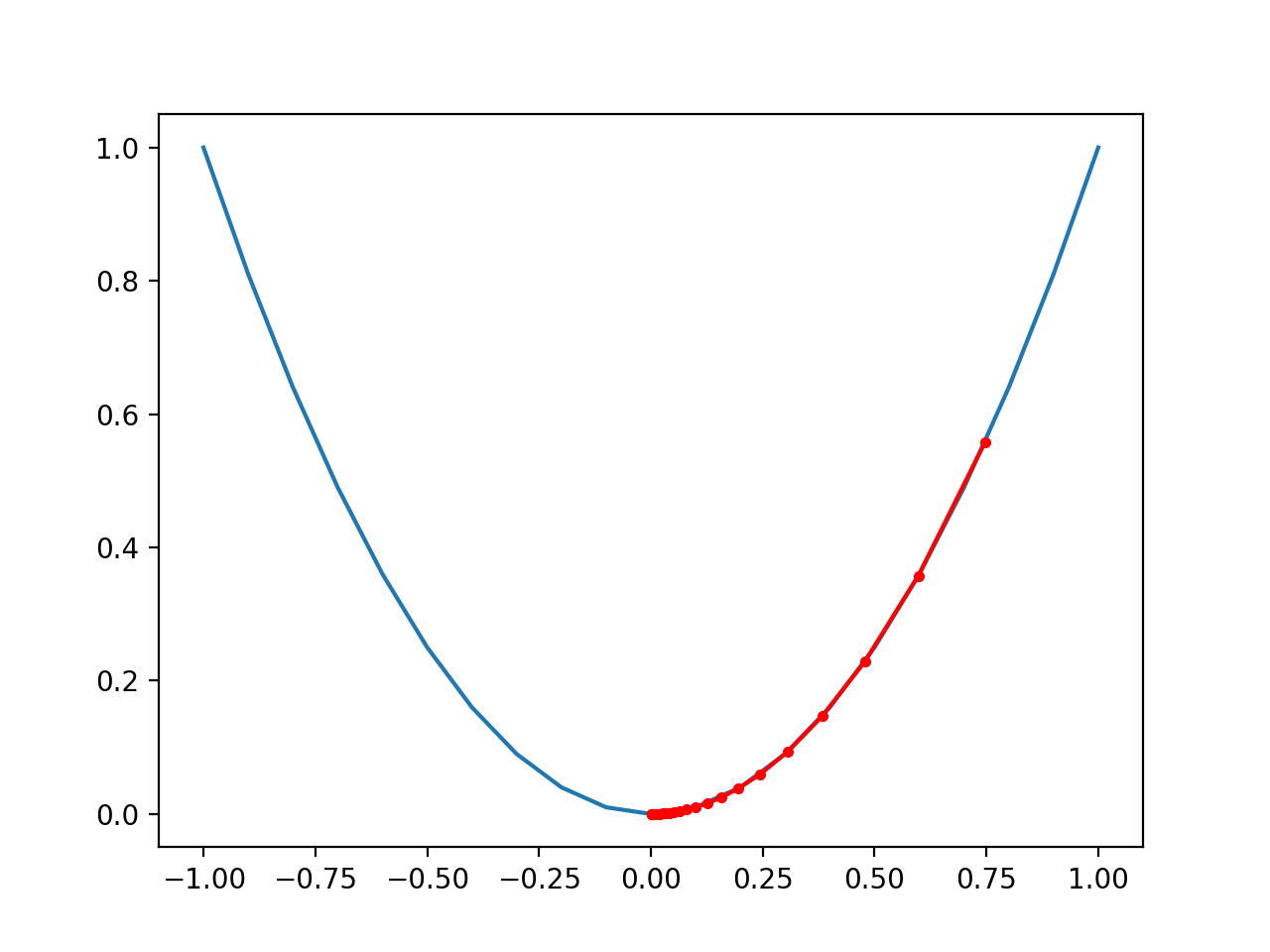
Running the example performs the gradient descent search with momentum on the objective function as before, except in this case, each point found during the search is plotted.
Nota: Your results may vary given the stochastic nature of the algorithm or evaluation procedure, or differences in numerical precision. Consider running the example a few times and compare the average outcome.
In this case, if we compare the plot to the plot created previously for the performance of gradient descent (without momentum), we can see that the search indeed reaches the optima in fewer steps, noted with fewer distinct red dots on the path to the bottom of the basin.

Plot of the Progress of Gradient Descent With Momentum on a One Dimensional Objective Function
As an extension, try different values for momentum, such as 0.8, and review the resulting plot.
Let me know what you discover in the comments below.
Further Reading
This section provides more resources on the topic if you are looking to go deeper.
Books
APIs
Articles
Resumen
In this tutorial, you discovered the gradient descent with momentum algorithm.
Specifically, you learned:
- Gradient descent is an optimization algorithm that uses the gradient of the objective function to navigate the search space.
- Gradient descent can be accelerated by using momentum from past updates to the search position.
- How to implement gradient descent optimization with momentum and develop an intuition for its behavior.
Do you have any questions?
Ask your questions in the comments below and I will do my best to answer.
