Los conjuntos son un método de aprendizaje de máquinas que combinan las predicciones de múltiples modelos en un esfuerzo por lograr un mejor rendimiento predictivo.
Hay muchos tipos diferentes de conjuntos, aunque todos los enfoques tienen dos propiedades clave: requieren que los modelos contribuyentes sean diferentes, de modo que cometan distintos errores y combinen las predicciones en un intento de aprovechar lo que cada modelo diferente hace bien.
Sin embargo, no está claro cómo los conjuntos logran esto, especialmente en el contexto de los problemas de clasificación y de modelización predictiva de tipo regresivo. Es importante desarrollar una intuición de lo que hacen exactamente los conjuntos cuando combinan las predicciones, ya que ayudará a elegir y configurar los modelos apropiados en los proyectos de modelización predictiva.
En este post, descubrirán la intuición detrás de cómo funcionan los métodos de aprendizaje en conjunto.
Después de leer este post, lo sabrás:
- Los métodos de aprendizaje en conjunto funcionan combinando las funciones de mapeo aprendidas por los miembros contribuyentes.
- Los conjuntos para la clasificación se entienden mejor por la combinación de los límites de decisión de los miembros.
- Los conjuntos para la regresión se entienden mejor con la combinación de los hiperplanos de los miembros.
Empecemos.

Desarrollar una intuición de cómo funciona el aprendizaje en conjunto
Foto de Marco Verch, algunos derechos reservados.
Resumen del Tutorial
Este tutorial está dividido en tres partes; son:
- ¿Cómo funcionan los conjuntos
- Intuición para los conjuntos de clasificación
- Intuición para los conjuntos de regresión
¿Cómo funcionan los conjuntos
El aprendizaje en conjunto se refiere a la combinación de las predicciones de dos o más modelos.
El objetivo de utilizar métodos de conjunto es mejorar la habilidad de las predicciones sobre la de cualquiera de los miembros contribuyentes.
Este objetivo es sencillo, pero no está tan claro cómo exactamente los métodos de conjunto son capaces de lograrlo.
Es importante desarrollar una intuición de cómo funcionan las técnicas de conjunto, ya que le ayudará a elegir y configurar métodos de conjunto específicos para una tarea de predicción y a interpretar sus resultados para encontrar formas alternativas de mejorar aún más el rendimiento.
Consideremos un simple conjunto que entrena dos modelos en muestras ligeramente diferentes del conjunto de datos de entrenamiento y promedia sus predicciones.
Cada uno de los modelos de los miembros puede utilizarse de manera independiente para hacer predicciones, aunque se espera que el promedio de sus predicciones mejore su rendimiento. Este sólo puede ser el caso si cada modelo hace diferentes predicciones.
Diferentes predicciones significan que en algunos casos, el modelo 1 cometerá pocos errores y el modelo 2 cometerá más errores, y lo contrario para otros casos. Promediando sus predicciones se busca reducir estos errores a través de las predicciones hechas por ambos modelos.
A su vez, para que los modelos hagan diferentes predicciones, deben hacer diferentes supuestos sobre el problema de la predicción. Más específicamente, deben aprender una función de mapeo diferente de las entradas a las salidas. Podemos lograrlo en el caso simple capacitando a cada modelo en una muestra diferente del conjunto de datos de capacitación, pero hay muchas maneras adicionales de lograr esta diferencia; la capacitación de diferentes tipos de modelos es una sola.
Estos elementos son cómo y los métodos de conjunto funcionan en el sentido general, es decir:
- Los miembros aprenden diferentes funciones de mapeo para el mismo problema. Esto es para asegurar que los modelos cometan diferentes errores de predicción.
- Las predicciones hechas por los miembros se combinan de alguna manera. Esto es para asegurar que se exploten las diferencias en los errores de predicción.
No nos limitamos a suavizar los errores de predicción, aunque sí podemos; en cambio, suavizamos la función de mapeo aprendida por los miembros contribuyentes.
La función de mapeo mejorada permite hacer mejores predicciones.
Este es un punto más profundo y es importante que lo entendamos. Veamos más de cerca lo que significa tanto para las tareas de clasificación como de regresión.
Intuición para los conjuntos de clasificación
El modelado predictivo de clasificación se refiere a los problemas en los que se debe predecir una etiqueta de clase a partir de ejemplos de entrada.
Un modelo puede predecir una etiqueta de clase nítida, por ejemplo, una variable categórica, o las probabilidades de todos los posibles resultados categóricos.
En el caso simple, las etiquetas de clase nítidas predichas por los miembros del conjunto pueden ser combinadas por votación, por ejemplo, el modo estadístico o la etiqueta con más votos determina el resultado del conjunto. Las probabilidades de clase predichas por los miembros del conjunto pueden ser sumadas y normalizadas.
Funcionalmente, algún proceso como éste se produce en un conjunto para una tarea de clasificación, pero el efecto es en la función de mapeo desde los ejemplos de entrada hasta las etiquetas de clase o las probabilidades. Sigamos con las etiquetas por ahora.
La forma más común de pensar en la función de mapeo para la clasificación es utilizando un gráfico en el que los datos de entrada representan un punto en un espacio de n dimensiones definido por la extensión de las variables de entrada, llamado espacio de características. Por ejemplo, si tuviéramos dos características de entrada, x e y, ambas en el rango de cero a uno, entonces el espacio de entrada sería un plano bidimensional y cada ejemplo en el conjunto de datos sería un punto en ese plano. A cada punto se le puede asignar un color o una forma basado en la etiqueta de la clase.
Un modelo que aprende a clasificar los puntos en efecto dibuja líneas en el espacio de las características para separar los ejemplos. Podemos tomar muestras de puntos en el espacio de los rasgos en una cuadrícula y obtener un mapa de cómo el modelo piensa que el espacio de los rasgos debe ser por cada etiqueta de clase.
La separación de los ejemplos en el espacio del rasgo por el modelo se denomina límite de decisión y un trazado de la cuadrícula o mapa de cómo el modelo clasifica los puntos en el espacio del rasgo se denomina un trazado de límite de decisión.
Ahora considera un conjunto en el que cada modelo tiene un mapeo diferente de entradas a salidas. En efecto, cada modelo tiene un límite de decisión diferente o una idea diferente de cómo dividirse en el espacio de características por etiqueta de clase. Cada modelo dibujará las líneas de forma diferente y cometerá diferentes errores.
Cuando combinamos las predicciones de estos múltiples modelos diferentes, estamos en efecto promediando los límites de decisión. Estamos definiendo un nuevo límite de decisión que intenta aprender de todas las diferentes opiniones sobre el espacio de características aprendidas por los miembros contribuyentes.
La siguiente figura tomada de la página 1 de «Ensemble Machine Learning» proporciona una descripción útil de esto.
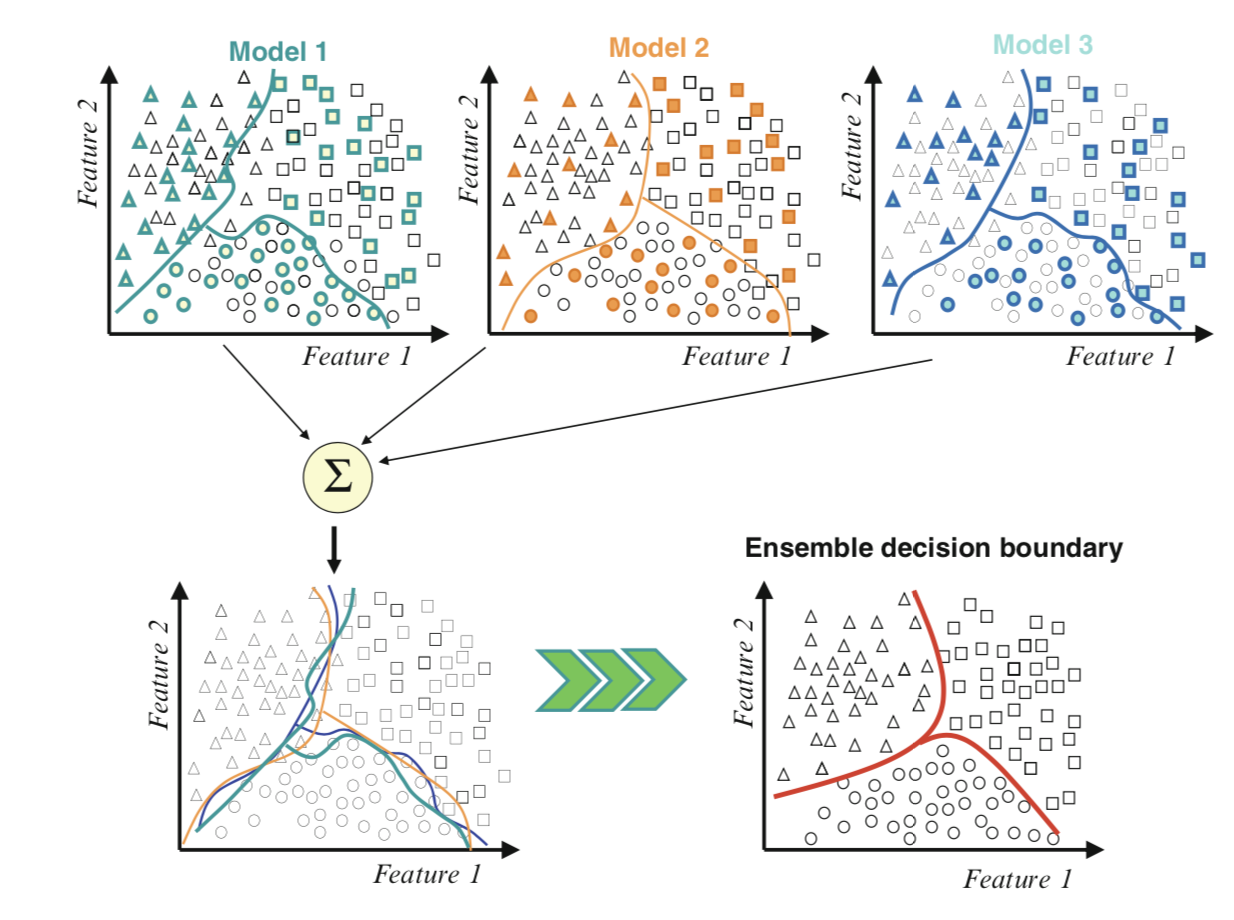
Ejemplo de combinación de límites de decisión usando un conjunto
Tomado de Ensemble Machine Learning, 2012.
Podemos ver a los miembros contribuyentes en la parte superior, cada uno con diferentes límites de decisión en el espacio de características. Luego la parte inferior izquierda dibuja todos los límites de decisión en la misma trama mostrando cómo se diferencian y cometen diferentes errores.
Por último, podemos combinar estos límites para crear un nuevo límite de decisión generalizado en la parte inferior derecha que capte mejor la división verdadera pero desconocida del espacio de las características, lo que se traduce en un mejor rendimiento predictivo.
Intuición para los conjuntos de regresión
El modelado predictivo de regresión se refiere a los problemas en los que se debe predecir un valor numérico a partir de ejemplos de entrada.
En el caso simple, las predicciones numéricas hechas por los miembros del conjunto pueden combinarse utilizando medidas estadísticas como la media, aunque pueden utilizarse combinaciones más complejas.
Al igual que la clasificación, el efecto del conjunto es que las funciones cartográficas de cada miembro contribuyente se promedian o combinan.
La forma más común de pensar en la función de mapeo para la regresión es usando un trazado lineal donde la variable de salida es otra dimensión añadida al espacio de la característica de entrada. La relación entre el espacio del rasgo y la dimensión de la variable de destino puede entonces resumirse como un hiperplano, por ejemplo, una línea en muchas dimensiones.
Esto es alucinante, así que consideremos el caso más simple en el que tenemos una entrada numérica y una salida numérica. Consideremos un plano o gráfico donde el eje x representa la característica de entrada y el eje y representa la variable objetivo. Podemos graficar cada ejemplo en el conjunto de datos como un punto en este gráfico.
Un modelo que aprende el mapeo desde la entrada a la salida aprende en efecto un hiperplano que conecta los puntos del espacio de la característica con la variable objetivo. Podemos muestrear una cuadrícula de puntos en el espacio del rasgo de entrada para idear valores para la variable objetivo y dibujar una línea para conectarlos para representar este hiperplano.
En nuestro caso bidimensional, esta es una línea que pasa por los puntos de la trama. Cualquier punto en el que la línea no pase por el gráfico representa un error de predicción y la distancia de la línea al punto es la magnitud del error.
Ahora considera un conjunto en el que cada modelo tiene un mapeo diferente de entradas a salidas. En efecto, cada modelo tiene un hiperplano diferente que conecta el espacio de características con el objetivo. Cada modelo dibujará diferentes líneas y cometerá diferentes errores con diferentes magnitudes.
Cuando combinamos las predicciones de estos múltiples modelos diferentes estamos, en efecto, promediando los hiperplanos. Estamos definiendo un nuevo hiperplano que intenta aprender de todas las diferentes características sobre cómo mapear las entradas a las salidas.
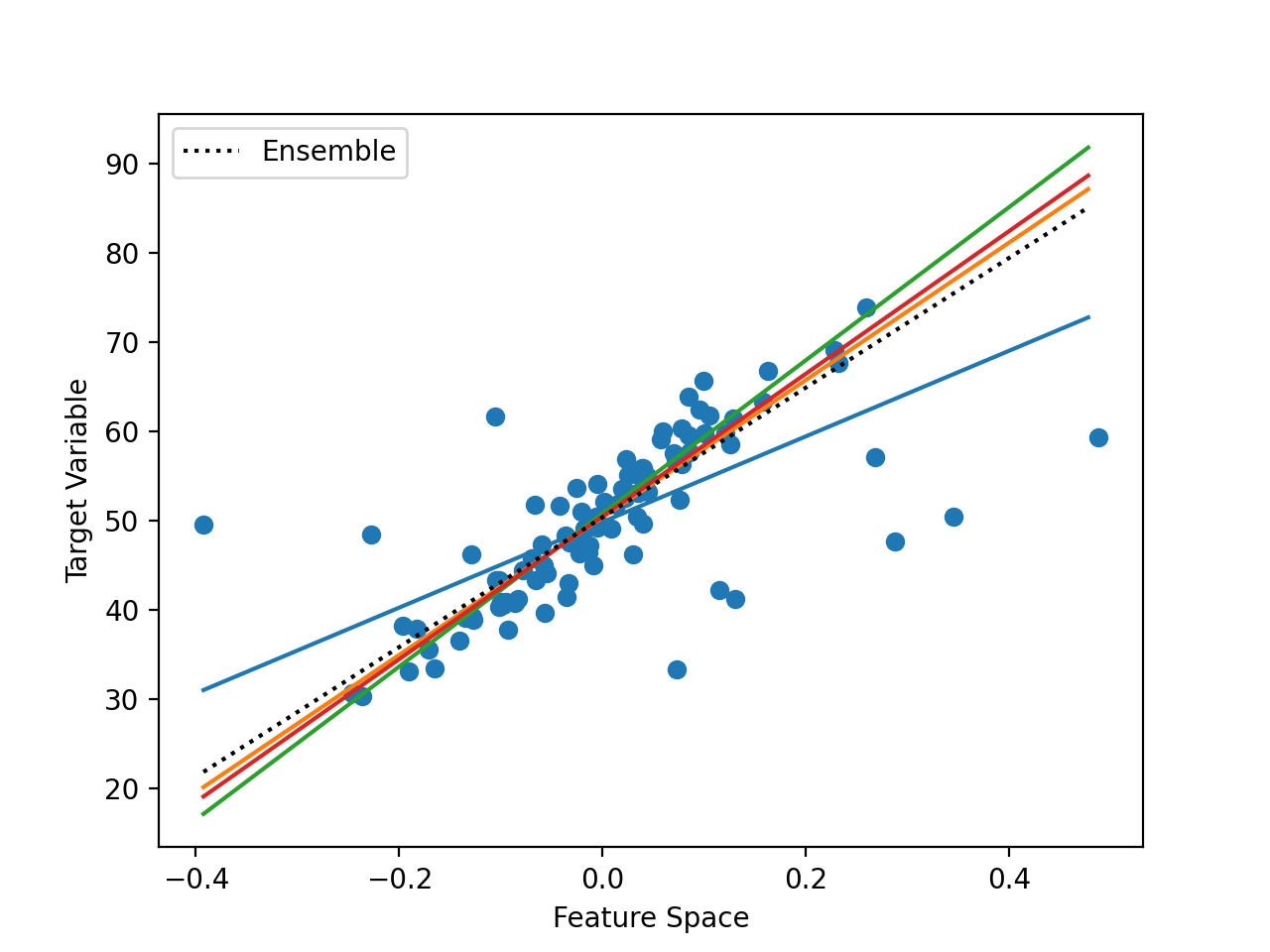
En la figura que figura a continuación se da un ejemplo de un espacio de características de entrada unidimensional y un espacio de destino con diferentes mapeos de hiperplanos aprendidos.

Ejemplo de combinación de hiperplanos usando un conjunto
Podemos ver los puntos que representan los puntos del conjunto de datos de entrenamiento. También podemos ver un número de diferentes líneas rectas a través de los datos. Los modelos no tienen que aprender las líneas rectas, pero en este caso, lo han hecho.
Finalmente, podemos ver una línea negra discontinua que muestra el promedio del conjunto de todos los modelos, lo que resulta en un menor error de predicción.
Más lecturas
Esta sección proporciona más recursos sobre el tema si desea profundizar en él.
Libros
Artículos
Resumen
En este post, descubriste la intuición detrás de cómo funcionan los métodos de aprendizaje en conjunto.
Específicamente, aprendiste:
- Los métodos de aprendizaje en conjunto funcionan combinando las funciones de mapeo aprendidas por los miembros contribuyentes.
- Los conjuntos para la clasificación se entienden mejor por la combinación de los límites de decisión de los miembros.
- Los conjuntos para la regresión se entienden mejor con la combinación de los hiperplanos de los miembros.
¿Tiene alguna pregunta?
Haga sus preguntas en los comentarios de abajo y haré lo posible por responder.
