Funciones de activación son una parte fundamental del diseño de una red neuronal.
La elección de la función de activación en la capa oculta controlará qué tan bien el modelo de red aprende el conjunto de datos de entrenamiento. La elección de la función de activación en la capa de salida definirá el tipo de predicciones que puede hacer el modelo.
Como tal, se debe hacer una elección cuidadosa de la función de activación para cada proyecto de red neuronal de aprendizaje profundo.
En este tutorial, descubrirá cómo elegir funciones de activación para modelos de redes neuronales.
Después de completar este tutorial, sabrá:
- Las funciones de activación son una parte clave del diseño de redes neuronales.
- La función de activación predeterminada moderna para capas ocultas es la función ReLU.
- La función de activación de las capas de salida depende del tipo de problema de predicción.
Empecemos.

Cómo elegir una función de activación para el aprendizaje profundo
Foto de Peter Dowley, algunos derechos reservados.
Descripción general del tutorial
Este tutorial se divide en tres partes; son:
- Funciones de activación
- Activación para capas ocultas
- Activación para capas de salida
Funciones de activación
Una función de activación en una red neuronal define cómo la suma ponderada de la entrada se transforma en una salida de un nodo o nodos en una capa de la red.
A veces, la función de activación se denomina «función de transferencia. » Si el rango de salida de la función de activación es limitado, entonces puede llamarse «función de aplastamiento. » Muchas funciones de activación no son lineales y pueden denominarse «no linealidad”En la capa o el diseño de la red.
La elección de la función de activación tiene un gran impacto en la capacidad y el rendimiento de la red neuronal, y pueden usarse diferentes funciones de activación en diferentes partes del modelo.
Técnicamente, la función de activación se usa dentro o después del procesamiento interno de cada nodo en la red, aunque las redes están diseñadas para usar la misma función de activación para todos los nodos en una capa.
Una red puede tener tres tipos de capas: capas de entrada que toman la entrada sin procesar del dominio, capas ocultas que toman la entrada de otra capa y pasan la salida a otra capa, y capas de salida que hacen una predicción.
Todas las capas ocultas suelen utilizar la misma función de activación. La capa de salida normalmente utilizará una función de activación diferente de las capas ocultas y depende del tipo de predicción requerida por el modelo.
Las funciones de activación también son típicamente diferenciables, lo que significa que la derivada de primer orden se puede calcular para un valor de entrada dado. Esto es necesario dado que las redes neuronales se entrenan típicamente usando el algoritmo de retropropagación de error que requiere la derivada del error de predicción para actualizar los pesos del modelo.
Hay muchos tipos diferentes de funciones de activación que se utilizan en las redes neuronales, aunque quizás solo se utilice una pequeña cantidad de funciones en la práctica para capas ocultas y de salida.
Echemos un vistazo a las funciones de activación utilizadas para cada tipo de capa.
Activación para capas ocultas
Una capa oculta en una red neuronal es una capa que recibe entrada de otra capa (como otra capa oculta o una capa de entrada) y proporciona salida a otra capa (como otra capa oculta o una capa de salida).
Una capa oculta no contacta directamente los datos de entrada ni produce salidas para un modelo, al menos en general.
Una red neuronal puede tener cero o más capas ocultas.
Normalmente, se utiliza una función de activación no lineal diferenciable en las capas ocultas de una red neuronal. Esto permite que el modelo aprenda funciones más complejas que una red entrenada mediante una función de activación lineal.
Para tener acceso a un espacio de hipótesis mucho más rico que se beneficiaría de representaciones profundas, necesita una función de no linealidad o activación.
– Página 72, Aprendizaje profundo con Python, 2017.
Quizás haya tres funciones de activación que quizás desee considerar para su uso en capas ocultas; son:
- Activación lineal rectificada (ReLU)
- Logística (Sigmoideo)
- Tangente hiperbólica (Tanh)
Esta no es una lista exhaustiva de las funciones de activación utilizadas para las capas ocultas, pero son las más utilizadas.
Echemos un vistazo más de cerca a cada uno de ellos.
Función de activación de capa oculta ReLU
La función de activación lineal rectificada, o función de activación ReLU, es quizás la función más común utilizada para capas ocultas.
Es común porque es simple de implementar y efectivo para superar las limitaciones de otras funciones de activación previamente populares, como Sigmoid y Tanh. En concreto, es menos susceptible a la desaparición de gradientes que impiden el entrenamiento de modelos profundos, aunque puede sufrir otros problemas como saturación o “muerto» unidades.
La función ReLU se calcula de la siguiente manera:
Esto significa que si el valor de entrada (x) es negativo, se devuelve un valor 0.0; de lo contrario, se devuelve el valor.
Puede obtener más información sobre los detalles de la función de activación de ReLU en este tutorial:
Podemos tener una intuición de la forma de esta función con el ejemplo resuelto a continuación.
|
# diagrama de ejemplo para la función de activación relu desde matplotlib importar pyplot # función lineal rectificada def rectificado(X): regreso max(0.0, X) # definir datos de entrada entradas = [[X para X en rango(–10, 10)] # calcular salidas salidas = [[rectificado(X) para X en entradas] # trazar entradas vs salidas pyplot.trama(entradas, salidas) pyplot.show() |
La ejecución del ejemplo calcula las salidas para un rango de valores y crea una gráfica de entradas versus salidas.
Podemos ver la forma de torcedura familiar de la función de activación de ReLU.
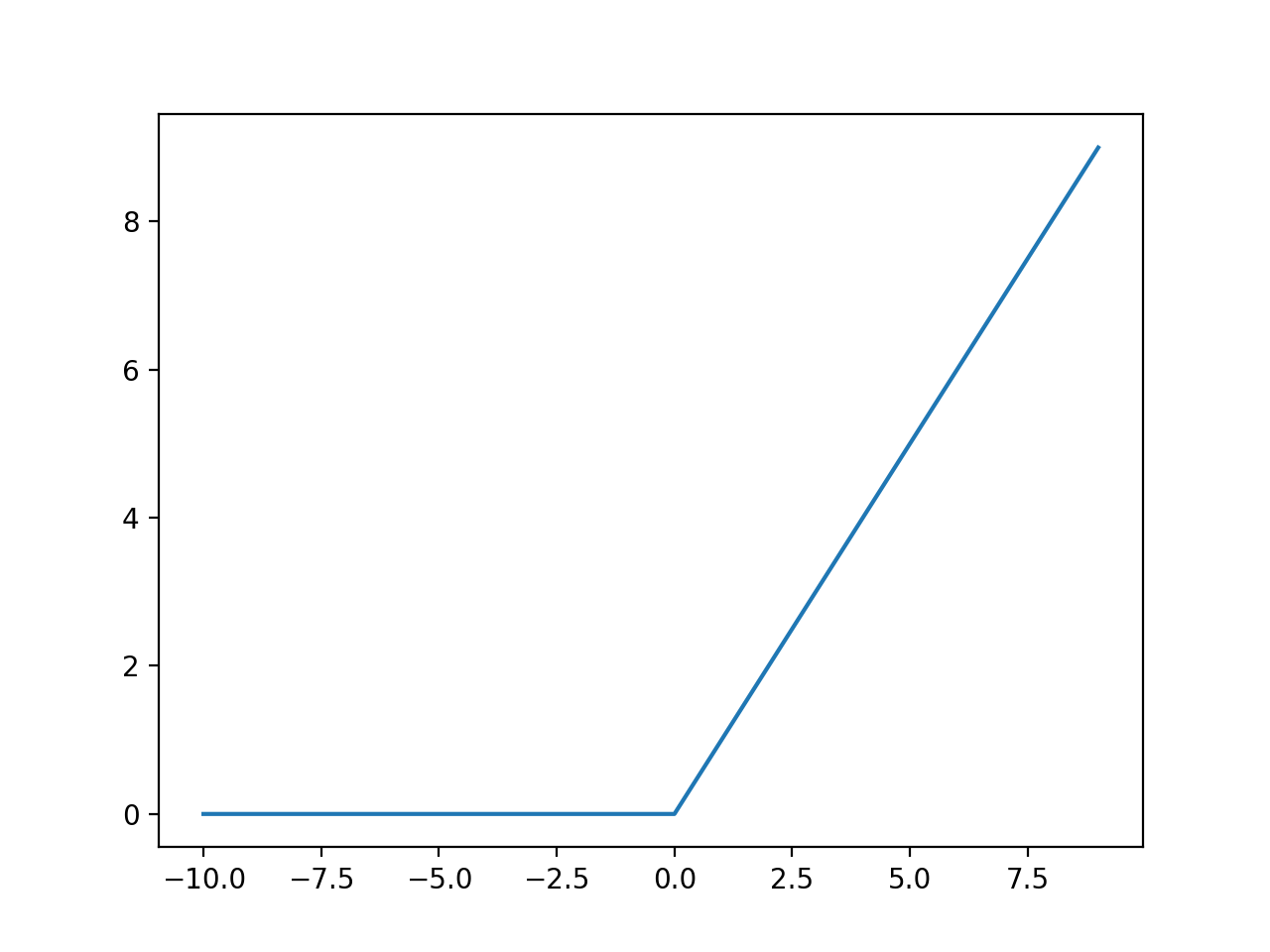
Gráfico de entradas frente a salidas para la función de activación de ReLU.
Al utilizar la función ReLU para capas ocultas, es una buena práctica utilizar un «El normal«O»El uniforme”Inicialización del peso y datos de entrada de la báscula en el rango 0-1 (normalizar) antes del entrenamiento.
Función de activación de capa oculta sigmoide
La función de activación sigmoidea también se denomina función logística.
Es la misma función que se utiliza en el algoritmo de clasificación de regresión logística.
La función toma cualquier valor real como entrada y genera valores en el rango de 0 a 1. Cuanto mayor sea la entrada (más positiva), más cerca estará el valor de salida a 1.0, mientras que cuanto más pequeña sea la entrada (más negativa), más cerca estará la salida será 0.0.
La función de activación sigmoidea se calcula de la siguiente manera:
Donde e es una constante matemática, que es la base del logaritmo natural.
Podemos tener una intuición de la forma de esta función con el ejemplo resuelto a continuación.
|
# gráfico de ejemplo para la función de activación sigmoidea desde matemáticas importar Exp desde matplotlib importar pyplot # función de activación sigmoidea def sigmoideo(X): regreso 1.0 / (1.0 + Exp(–X)) # definir datos de entrada entradas = [[X para X en rango(–10, 10)] # calcular salidas salidas = [[sigmoideo(X) para X en entradas] # trazar entradas vs salidas pyplot.trama(entradas, salidas) pyplot.show() |
La ejecución del ejemplo calcula las salidas para un rango de valores y crea una gráfica de entradas versus salidas.
Podemos ver la familiar forma de S de la función de activación sigmoidea.
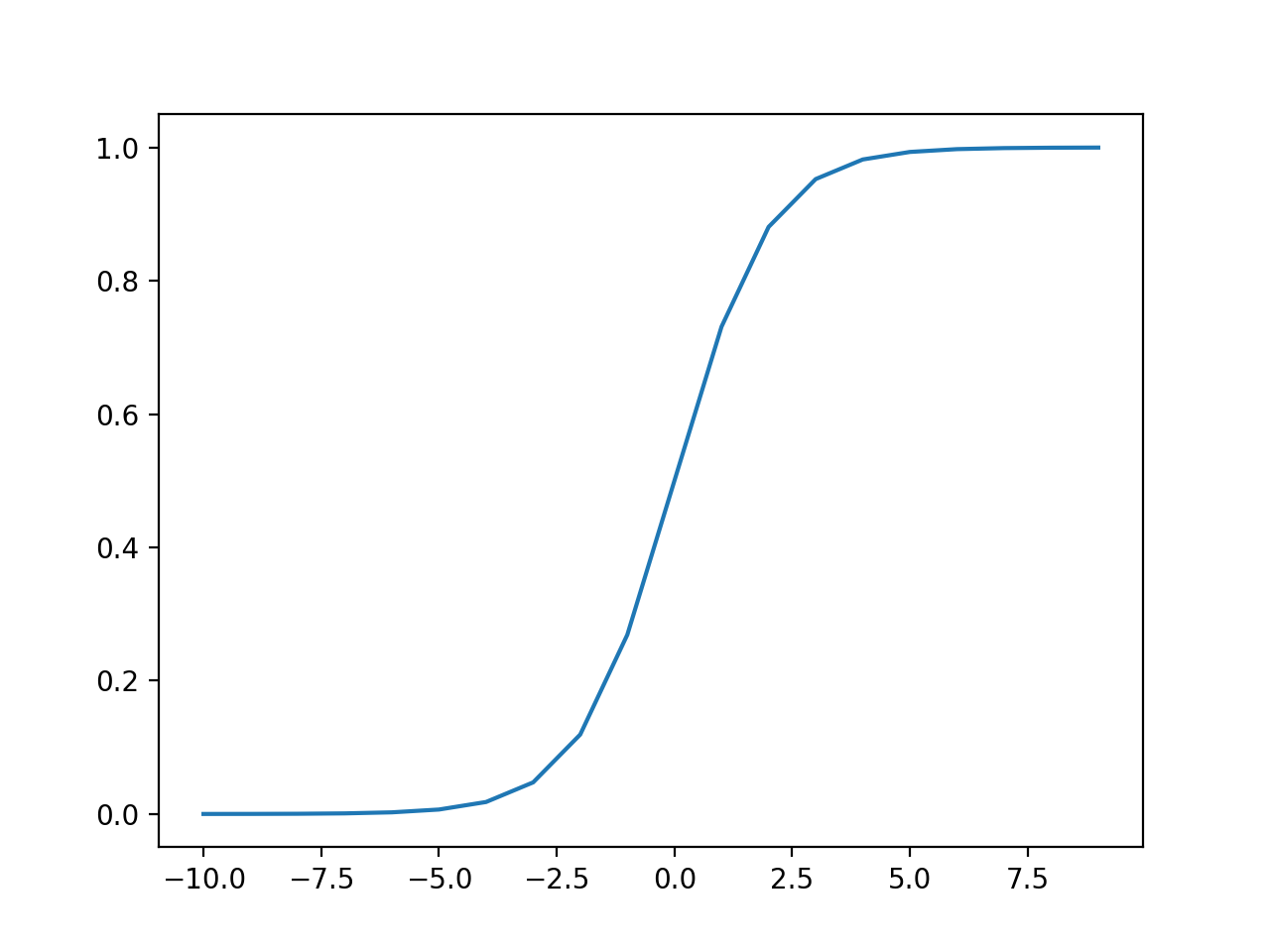
Gráfico de entradas frente a salidas para la función de activación sigmoidea.
Cuando se utiliza la función Sigmoide para capas ocultas, es una buena práctica utilizar un «Xavier Normal«O»Uniforme Xavier”Inicialización de peso (también denominada inicialización de Glorot, llamada así por Xavier Glorot) y datos de entrada de la báscula al rango 0-1 (por ejemplo, el rango de la función de activación) antes del entrenamiento.
Función de activación de capa oculta de Tanh
La función de activación de la tangente hiperbólica también se conoce simplemente como Tanh (también «tanh«Y»TanH“) Función.
Es muy similar a la función de activación sigmoidea e incluso tiene la misma forma de S.
La función toma cualquier valor real como valores de entrada y de salida en el rango de -1 a 1. Cuanto mayor sea la entrada (más positiva), más cerca estará el valor de salida a 1.0, mientras que cuanto menor sea la entrada (más negativa), más cerca la salida será -1.0.
La función de activación de Tanh se calcula de la siguiente manera:
- (e ^ x – e ^ -x) / (e ^ x + e ^ -x)
Donde e es una constante matemática que es la base del logaritmo natural.
Podemos tener una intuición de la forma de esta función con el ejemplo resuelto a continuación.
|
# gráfico de ejemplo para la función de activación de tanh desde matemáticas importar Exp desde matplotlib importar pyplot # función de activación de tanh def tanh(X): regreso (Exp(X) – Exp(–X)) / (Exp(X) + Exp(–X)) # definir datos de entrada entradas = [[X para X en rango(–10, 10)] # calcular salidas salidas = [[tanh(X) para X en entradas] # trazar entradas vs salidas pyplot.trama(entradas, salidas) pyplot.show() |
La ejecución del ejemplo calcula las salidas para un rango de valores y crea una gráfica de entradas versus salidas.
Podemos ver la familiar forma de S de la función de activación de Tanh.
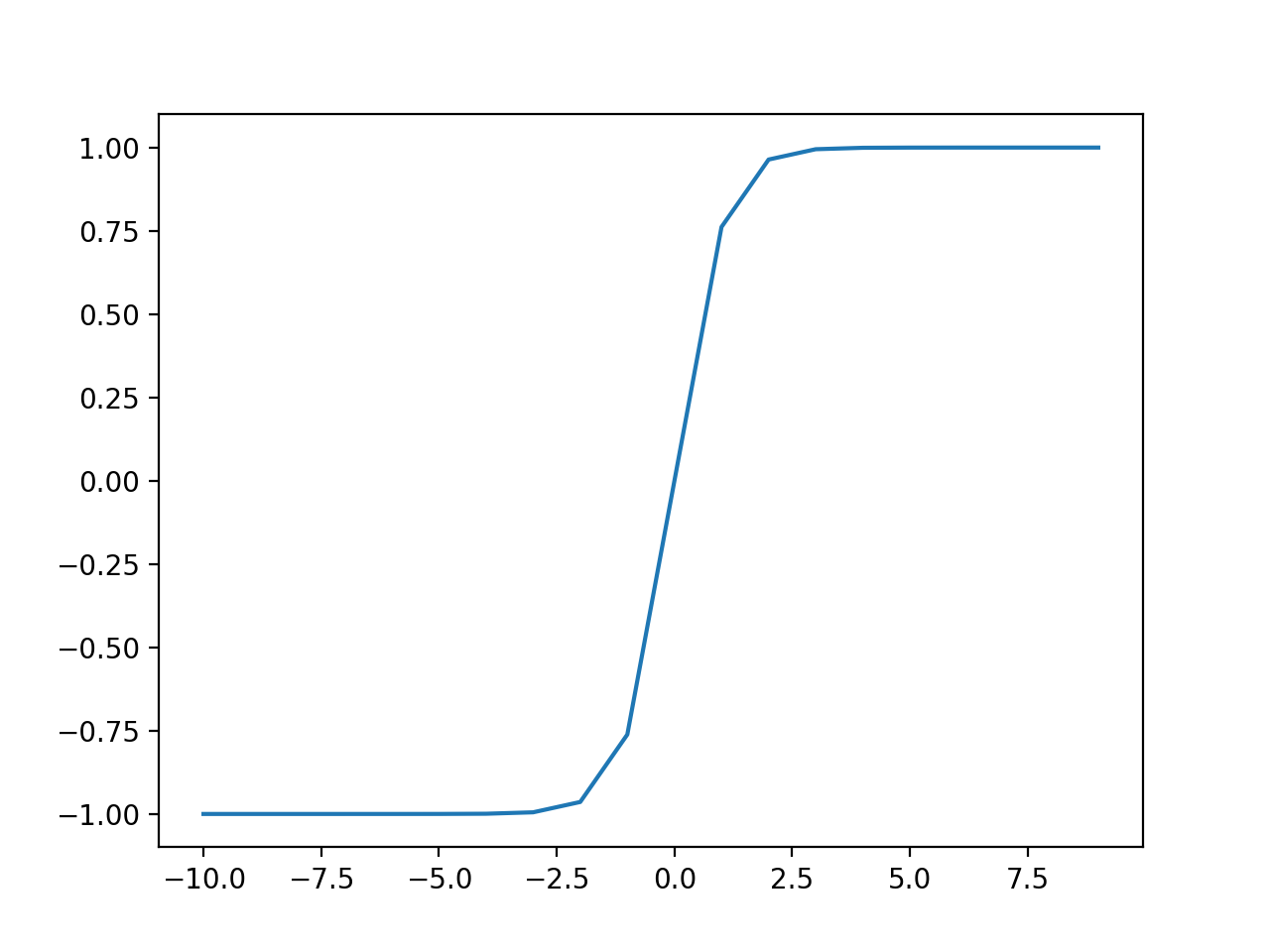
Gráfico de entradas y salidas para la función de activación de Tanh.
Al utilizar la función TanH para capas ocultas, es una buena práctica utilizar un «Xavier Normal«O»Uniforme Xavier”Inicialización de peso (también denominada inicialización de Glorot, llamada así por Xavier Glorot) y datos de entrada de escala en el rango de -1 a 1 (por ejemplo, el rango de la función de activación) antes del entrenamiento.
Cómo elegir una función de activación de capa oculta
Una red neuronal casi siempre tendrá la misma función de activación en todas las capas ocultas.
Es muy inusual variar la función de activación a través de un modelo de red.
Tradicionalmente, la función de activación sigmoidea era la función de activación predeterminada en la década de 1990. Quizás desde mediados hasta finales de la década de 1990 hasta la de 2010, la función Tanh fue la función de activación predeterminada para las capas ocultas.
… la función de activación de la tangente hiperbólica normalmente funciona mejor que la sigmoide logística.
– Página 195, Deep Learning, 2016.
Tanto la función sigmoidea como la de Tanh pueden hacer que el modelo sea más susceptible a problemas durante el entrenamiento, a través del llamado problema de gradientes de fuga.
Puede obtener más información sobre este problema en este tutorial:
La función de activación utilizada en las capas ocultas se elige típicamente en función del tipo de arquitectura de red neuronal.
Los modelos de redes neuronales modernas con arquitecturas comunes, como MLP y CNN, utilizarán la función de activación de ReLU o extensiones.
En las redes neuronales modernas, la recomendación predeterminada es utilizar la unidad lineal rectificada o ReLU …
– Página 174, Deep Learning, 2016.
Las redes recurrentes todavía usan comúnmente funciones de activación sigmoidea o Tanh, o incluso ambas. Por ejemplo, el LSTM comúnmente usa la activación Sigmoid para conexiones recurrentes y la activación Tanh para salida.
- Perceptrón multicapa (MLP): Función de activación de ReLU.
- Red neuronal convolucional (CNN): Función de activación de ReLU.
- Red neuronal recurrente: Función de activación de Tanh y / o Sigmoide.
Si no está seguro de qué función de activación utilizar para su red, pruebe algunas y compare los resultados.
La siguiente figura resume cómo elegir una función de activación para las capas ocultas de su modelo de red neuronal.
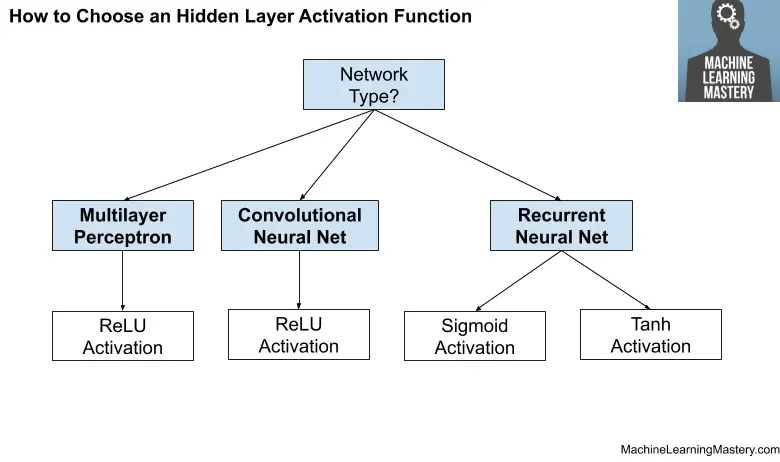
Cómo elegir una función de activación de capa oculta
Activación para capas de salida
La capa de salida es la capa en un modelo de red neuronal que genera directamente una predicción.
Todos los modelos de redes neuronales de retroalimentación tienen una capa de salida.
Quizás haya tres funciones de activación que quizás desee considerar para su uso en la capa de salida; son:
- Lineal
- Logística (sigmoidea)
- Softmax
Esta no es una lista exhaustiva de las funciones de activación utilizadas para las capas de salida, pero son las más utilizadas.
Echemos un vistazo más de cerca a cada uno de ellos.
Función de activación de salida lineal
La función de activación lineal también se denomina «identidad«(Multiplicado por 1,0) o»sin activación. «
Esto se debe a que la función de activación lineal no cambia la suma ponderada de la entrada de ninguna manera y en su lugar devuelve el valor directamente.
Podemos tener una intuición de la forma de esta función con el ejemplo resuelto a continuación.
|
# gráfico de ejemplo para la función de activación lineal desde matplotlib importar pyplot # función de activación lineal def lineal(X): regreso X # definir datos de entrada entradas = [[X para X en rango(–10, 10)] # calcular salidas salidas = [[lineal(X) para X en entradas] # trazar entradas vs salidas pyplot.trama(entradas, salidas) pyplot.show() |
La ejecución del ejemplo calcula las salidas para un rango de valores y crea una gráfica de entradas versus salidas.
Podemos ver una forma de línea diagonal donde las entradas se trazan contra salidas idénticas.
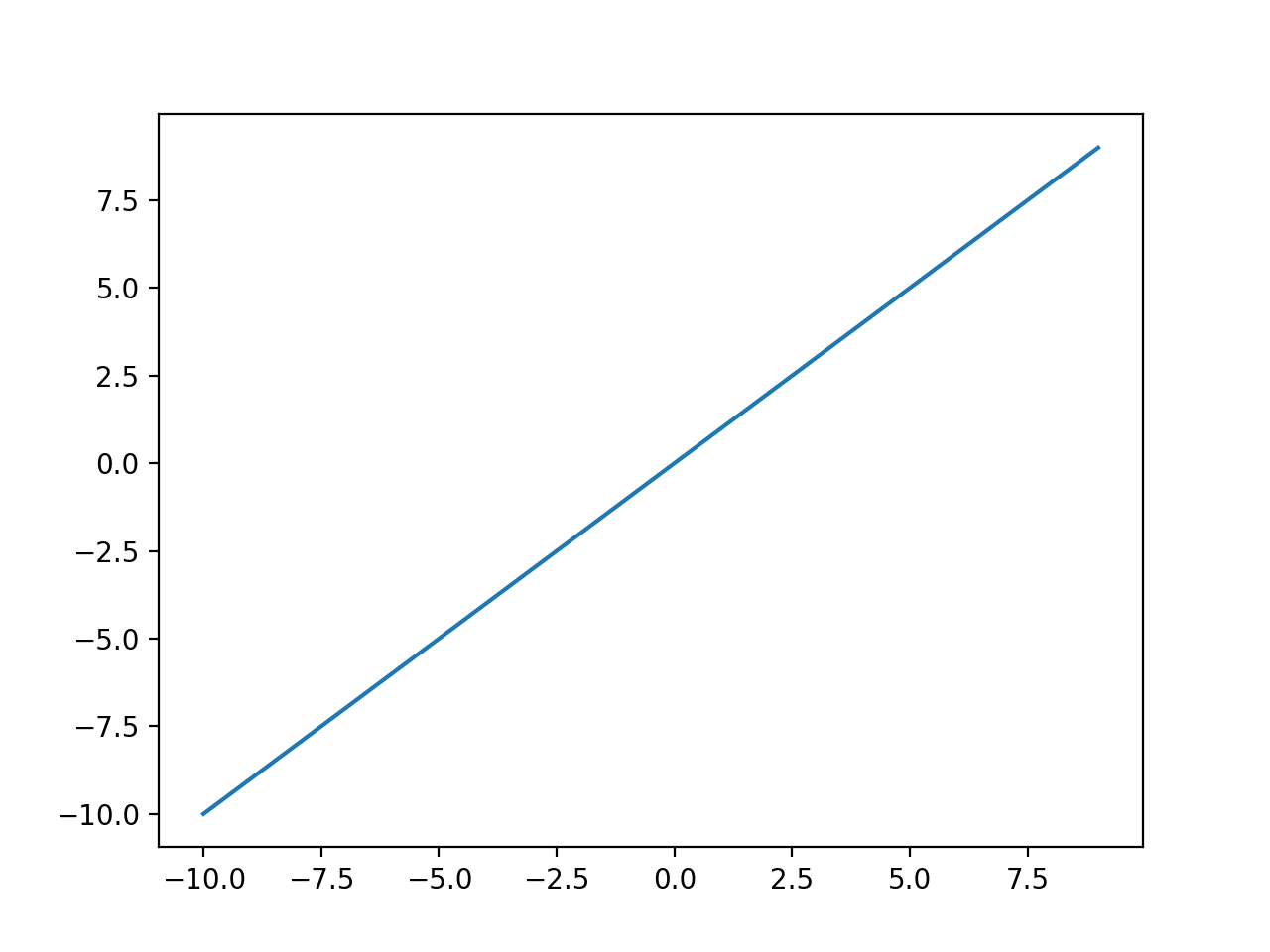
Gráfico de entradas y salidas para la función de activación lineal
Los valores objetivo que se utilizan para entrenar un modelo con una función de activación lineal en la capa de salida normalmente se escalan antes del modelado mediante normalización o transformaciones de estandarización.
Función de activación de salida sigmoidea
La función sigmoidea de activación logística se describió en la sección anterior.
Sin embargo, para agregar algo de simetría, podemos revisar la forma de esta función con el ejemplo resuelto a continuación.
|
# gráfico de ejemplo para la función de activación sigmoidea desde matemáticas importar Exp desde matplotlib importar pyplot # función de activación sigmoidea def sigmoideo(X): regreso 1.0 / (1.0 + Exp(–X)) # definir datos de entrada entradas = [[X para X en rango(–10, 10)] # calcular salidas salidas = [[sigmoideo(X) para X en entradas] # trazar entradas vs salidas pyplot.trama(entradas, salidas) pyplot.show() |
La ejecución del ejemplo calcula las salidas para un rango de valores y crea una gráfica de entradas versus salidas.
Podemos ver la familiar forma de S de la función de activación sigmoidea.

Gráfico de entradas frente a salidas para la función de activación sigmoidea.
Las etiquetas de destino utilizadas para entrenar un modelo con una función de activación sigmoidea en la capa de salida tendrán los valores 0 o 1.
Función de activación de salida Softmax
La función softmax genera un vector de valores que suman 1.0 que pueden interpretarse como probabilidades de pertenencia a una clase.
Está relacionado con la función argmax que genera un 0 para todas las opciones y un 1 para la opción elegida. Softmax es un «mas suave”Versión de argmax que permite una salida similar a la probabilidad de una función de ganador se lleva todo.
Como tal, la entrada a la función es un vector de valores reales y la salida es un vector de la misma longitud con valores que suman 1.0 probabilidades similares.
La función softmax se calcula de la siguiente manera:
Dónde X es un vector de salidas ye es una constante matemática que es la base del logaritmo natural.
Puede obtener más información sobre los detalles de la función Softmax en este tutorial:
No podemos trazar la función softmax, pero podemos dar un ejemplo de cómo calcularla en Python.
|
# función de activación softmax def softmax(X): regreso Exp(X) / Exp(X).suma() # definir datos de entrada entradas = [[1.0, 3,0, 2.0] # calcular salidas salidas = softmax(entradas) # reporta las probabilidades impresión(salidas) # reporta la suma de las probabilidades impresión(salidas.suma()) |
La ejecución del ejemplo calcula la salida softmax para el vector de entrada.
Luego confirmamos que la suma de las salidas del softmax suma efectivamente el valor 1.0.
|
[0.09003057 0.66524096 0.24472847]
1.0 |
Las etiquetas de destino utilizadas para entrenar un modelo con la función de activación softmax en la capa de salida serán vectores con 1 para la clase de destino y 0 para todas las demás clases.
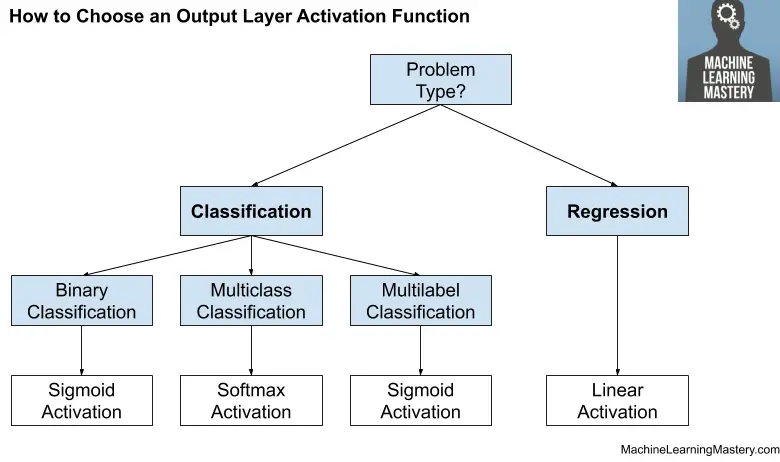
Cómo elegir una función de activación de salida
Debe elegir la función de activación para su capa de salida según el tipo de problema de predicción que está resolviendo.
Específicamente, el tipo de variable que se predice.
Por ejemplo, puede dividir los problemas de predicción en dos grupos principales, prediciendo una variable categórica (clasificación) y predecir una variable numérica (regresión).
Si su problema es un problema de regresión, debe utilizar una función de activación lineal.
- Regresión: Un nodo, activación lineal.
Si su problema es un problema de clasificación, existen tres tipos principales de problemas de clasificación y cada uno puede usar una función de activación diferente.
Predecir una probabilidad no es un problema de regresión; es clasificación. En todos los casos de clasificación, su modelo predecirá la probabilidad de pertenencia a una clase (por ejemplo, la probabilidad de que un ejemplo pertenezca a cada clase) que puede convertir en una etiqueta de clase nítida redondeando (para sigmoide) o argmax (para softmax).
Si hay dos clases mutuamente excluyentes (clasificación binaria), entonces su capa de salida tendrá un nodo y se debe usar una función de activación sigmoidea. Si hay más de dos clases mutuamente excluyentes (clasificación multiclase), entonces su capa de salida tendrá un nodo por clase y se debe usar una activación softmax. Si hay dos o más clases mutuamente inclusivas (clasificación de múltiples etiquetas), entonces su capa de salida tendrá un nodo para cada clase y se utilizará una función de activación sigmoidea.
- Clasificación binaria: Un nodo, activación sigmoidea.
- Clasificación multiclase: Un nodo por clase, activación softmax.
- Clasificación de múltiples etiquetas: Un nodo por clase, activación sigmoidea.
La siguiente figura resume cómo elegir una función de activación para la capa de salida de su modelo de red neuronal.

Cómo elegir una función de activación de la capa de salida
Otras lecturas
Esta sección proporciona más recursos sobre el tema si está buscando profundizar.
Tutoriales
Libros
Artículos
Resumen
En este tutorial, descubrió cómo elegir funciones de activación para modelos de redes neuronales.
Específicamente, aprendiste:
- Las funciones de activación son una parte clave del diseño de redes neuronales.
- La función de activación predeterminada moderna para capas ocultas es la función ReLU.
- La función de activación de las capas de salida depende del tipo de problema de predicción.
¿Tiene usted alguna pregunta?
Haga sus preguntas en los comentarios a continuación y haré todo lo posible para responder.

