Puede resultar complicado desarrollar un modelo predictivo de red neuronal para un nuevo conjunto de datos.
Un enfoque es inspeccionar primero el conjunto de datos y desarrollar ideas sobre qué modelos podrían funcionar, luego explorar la dinámica de aprendizaje de modelos simples en el conjunto de datos y finalmente desarrollar y ajustar un modelo para el conjunto de datos con un arnés de prueba robusto.
Este proceso se puede utilizar para desarrollar modelos de redes neuronales eficaces para problemas de modelado predictivo de clasificación y regresión.
En este tutorial, descubrirá cómo desarrollar un modelo de red neuronal de perceptrón multicapa para el conjunto de datos de clasificación binaria de la ionosfera.
Después de completar este tutorial, sabrá:
- Cómo cargar y resumir el conjunto de datos de la ionosfera y usar los resultados para sugerir preparaciones de datos y configuraciones de modelos para usar.
- Cómo explorar la dinámica de aprendizaje de modelos MLP simples en el conjunto de datos.
- Cómo desarrollar estimaciones sólidas del rendimiento del modelo, ajustar el rendimiento del modelo y hacer predicciones sobre nuevos datos.
Empecemos.

Cómo desarrollar una red neuronal para predecir perturbaciones en la ionosfera
Foto de Sergey Pesterev, algunos derechos reservados.
Descripción general del tutorial
Este tutorial se divide en cuatro partes; son:
- Conjunto de datos de clasificación binaria de ionosfera
- Dinámica de aprendizaje de redes neuronales
- Evaluación y ajuste de modelos MLP
- Modelo final y hacer predicciones
Conjunto de datos de clasificación binaria de ionosfera
El primer paso es definir y explorar el conjunto de datos.
Trabajaremos con el «Ionosfera”Conjunto de datos de clasificación binaria estándar.
Este conjunto de datos implica predecir si una estructura está en la atmósfera o no dados los retornos de radar.
Puede obtener más información sobre el conjunto de datos aquí:
Puede ver las primeras filas del conjunto de datos a continuación.
|
1,0,0.99539, -0.05889,0.85243,0.02306,0.83398, -0.37708,1,0.03760,0.85243, -0.17755,0.59755, -0.44945,0.60536, -0.38223,0.84356, -0.38542,0.58212, -0.32192,0.56971, – 0.29674,0.36946, -0.47357,0.56811, -0.51171,0.41078, -0.46168,0.21266, -0.34090,0.42267, -0.54487,0.18641, -0.45300, g 1,0,1, -0.18829,0.93035, -0.36156, -0.10868, -0.93597,1, -0.04549,0.50874, -0.67743,0.34432, -0.69707, -0.51685, -0.97515,0.05499, -0.62237,0.33109, -1 , -0.13151, -0.45300, -0.18056, -0.35734, -0.20332, -0.26569, -0.20468, -0.18401, -0.19040, -0.11593, -0.16626, -0.06288, -0.13738, -0.02447, b 1,0,1, -0.03365,1,0.00485,1, -0.12062,0.88965,0.01198,0.73082,0.05346,0.85443,0.00827,0.54591,0.00299,0.83775, -0.13644,0.75535, -0.08540,0.70887, -0.27502,0.43385 , -0.12062,0.57528, -0.40220,0.58984, -0.22145,0.43100, -0.17365,0.60436, -0.24180,0.56045, -0.38238, g 1,0,1, -0.45161,1,1,0.71216, -1,0,0,0,0,0,0, -1,0.14516,0.54094, -0.39330, -1, -0.54467, -0.69975,1 , 0,0,1,0.90695,0.51613,1,1, -0.20099,0.25682,1, -0.32382,1, b 1,0,1, -0.02401,0.94140,0.06531,0.92106, -0.23255,0.77152, -0.16399,0.52798, -0.20275,0.56409, -0.00712,0.34395, -0.27457,0.52940, -0.21780,0.45107, -0.17813,0.05982, -0.35575,0.02309, -0.52879,0.03286, -0.65158,0.13290, -0.53206,0.02431, -0.62197, -0.05707, -0.59573, -0.04608, -0.65697, g … |
Podemos ver que los valores son todos numéricos y quizás en el rango [-1, 1]. Esto sugiere que probablemente no sea necesario algún tipo de escala.
También podemos ver que la etiqueta es una cadena («gramo» y «segundo“), Lo que sugiere que los valores deberán codificarse en 0 y 1 antes de ajustar un modelo.
Podemos cargar el conjunto de datos como un DataFrame de pandas directamente desde la URL; por ejemplo:
|
# cargue el conjunto de datos de ionosfera y resuma la forma de pandas importar leer_csv # definir la ubicación del conjunto de datos url = ‘https://raw.githubusercontent.com/jbrownlee/Datasets/master/ionosphere.csv’ # cargar el conjunto de datos df = read_csv(url, encabezamiento=Ninguno) # resumir forma imprimir(df.forma) |
La ejecución del ejemplo carga el conjunto de datos directamente desde la URL e informa la forma del conjunto de datos.
En este caso, podemos ver que el conjunto de datos tiene 35 variables (34 de entrada y una salida) y que el conjunto de datos tiene 351 filas de datos.
No se trata de muchas filas de datos para una red neuronal y sugiere que una red pequeña, quizás con regularización, sería apropiada.
También sugiere que usar la validación cruzada de k-fold sería una buena idea dado que dará una estimación más confiable del rendimiento del modelo que una división de tren / prueba y porque un solo modelo encajará en segundos en lugar de horas o días con el conjuntos de datos más grandes.
A continuación, podemos obtener más información sobre el conjunto de datos observando estadísticas resumidas y una gráfica de los datos.
|
# mostrar estadísticas resumidas y gráficos del conjunto de datos de la ionosfera de pandas importar read_csv de matplotlib importar pyplot # definir la ubicación del conjunto de datos url = ‘https://raw.githubusercontent.com/jbrownlee/Datasets/master/ionosphere.csv’ # cargar el conjunto de datos df = read_csv(url, encabezamiento=Ninguno) # mostrar estadísticas resumidas imprimir(df.describir()) # trazar histogramas df.hist() pyplot.show() |
Ejecutar el ejemplo primero carga los datos antes y luego imprime estadísticas de resumen para cada variable.
Podemos ver que los valores medios para cada variable están en decenas, con valores que van de -1 a 1. Esto confirma que probablemente no sea necesario escalar los datos.
|
0 1 2 … 31 32 33 recuento 351.000000 351.0 351.000000 … 351.000000 351.000000 351.000000 media 0.891738 0.0 0.641342 … -0.003794 0.349364 0.014480 estándar 0.311155 0.0 0.497708 … 0.513574 0.522663 0.468337 min 0,000000 0,0 -1,000000 … -1,000000 -1,000000 -1,000000 25% 1.000000 0.0 0.472135 … -0.242595 0.000000 -0.165350 50% 1.000000 0.0 0.871110 … 0.000000 0.409560 0.000000 75% 1.000000 0.0 1.000000 … 0.200120 0.813765 0.171660 máx 1.000000 0.0 1.000000 … 1.000000 1.000000 1.000000 |
Luego se crea un gráfico de histograma para cada variable.
Podemos ver que muchas variables tienen una distribución gaussiana o similar a la gaussiana.
Es posible que tengamos algún beneficio al usar una transformada de potencia en cada variable para hacer que la distribución de probabilidad sea menos sesgada, lo que probablemente mejorará el rendimiento del modelo.
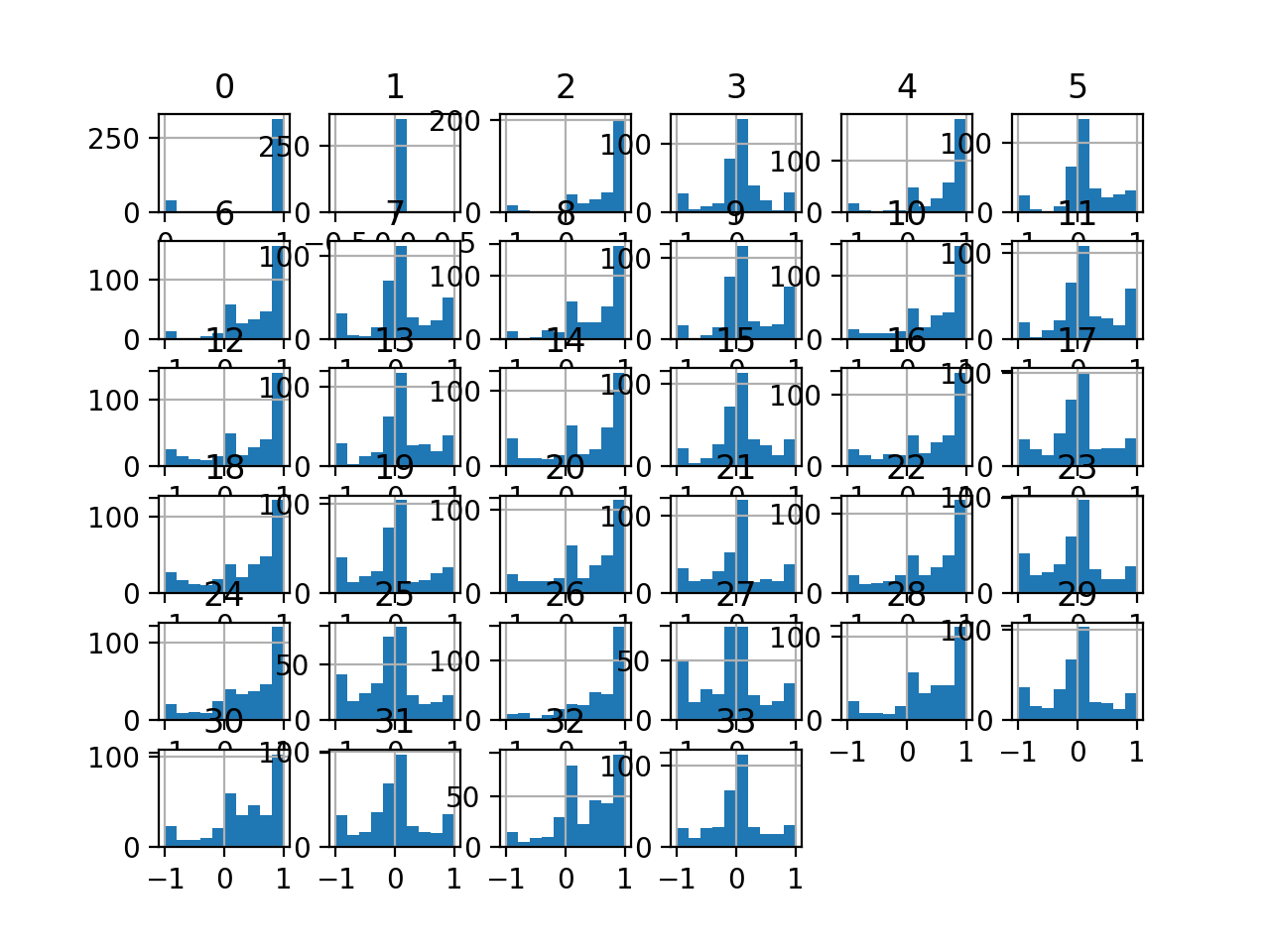
Histogramas del conjunto de datos de clasificación de ionosfera
Ahora que estamos familiarizados con el conjunto de datos, exploremos cómo podríamos desarrollar un modelo de red neuronal.
Dinámica de aprendizaje de redes neuronales
Desarrollaremos un modelo de perceptrón multicapa (MLP) para el conjunto de datos utilizando TensorFlow.
No podemos saber qué modelo de arquitectura de hiperparámetros de aprendizaje sería bueno o mejor para este conjunto de datos, por lo que debemos experimentar y descubrir qué funciona bien.
Dado que el conjunto de datos es pequeño, un tamaño de lote pequeño probablemente sea una buena idea, p. Ej. 16 o 32 filas. Usar la versión de Adam del descenso de gradiente estocástico es una buena idea al comenzar, ya que adapta automáticamente la tasa de aprendizaje y funciona bien en la mayoría de los conjuntos de datos.
Antes de evaluar los modelos en serio, es una buena idea revisar la dinámica de aprendizaje y ajustar la arquitectura del modelo y la configuración de aprendizaje hasta que tengamos una dinámica de aprendizaje estable, luego buscar sacar el máximo provecho del modelo.
Podemos hacer esto mediante el uso de una simple división de tren / prueba de los datos y revisar los gráficos de las curvas de aprendizaje. Esto nos ayudará a ver si estamos aprendiendo demasiado o mal; entonces podemos adaptar la configuración en consecuencia.
Primero, debemos asegurarnos de que todas las variables de entrada sean valores de punto flotante y codificar la etiqueta de destino como valores enteros 0 y 1.
|
... # asegúrese de que todos los datos sean valores de punto flotante X = X.astipo(‘float32’) # codificar cadenas a números enteros y = LabelEncoder().fit_transform(y) |
A continuación, podemos dividir el conjunto de datos en variables de entrada y salida, luego en 67/33 conjuntos de entrenamiento y prueba.
|
... # dividir en columnas de entrada y salida X, y = df.valores[[:, :–1], df.valores[[:, –1] # dividir en conjuntos de datos de prueba y de tren X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0,33) |
Podemos definir un modelo MLP mínimo. En este caso, usaremos una capa oculta con 10 nodos y una capa de salida (elegida arbitrariamente). Usaremos la función de activación de ReLU en la capa oculta y el «él_normal”Inicialización del peso, ya que juntos son una buena práctica.
La salida del modelo es una activación sigmoidea para la clasificación binaria y minimizaremos la pérdida de entropía cruzada binaria.
|
... # determinar el número de características de entrada n_features = X.forma[[1] # definir modelo modelo = Secuencial() modelo.agregar(Denso(10, activación=‘relu’, kernel_initializer=‘él_normal’, input_shape=(n_features,))) modelo.agregar(Denso(1, activación=‘sigmoideo’)) # compilar el modelo modelo.compilar(optimizador=‘Adán’, pérdida=‘binary_crossentropy’) |
Ajustaremos el modelo para 200 épocas de entrenamiento (elegidas arbitrariamente) con un tamaño de lote de 32 porque es un conjunto de datos pequeño.
Estamos ajustando el modelo a datos sin procesar, lo que creemos que podría ser una buena idea, pero es un punto de partida importante.
|
... # se ajusta al modelo historia = modelo.encajar(X_train, y_train, épocas=200, tamaño del lote=32, verboso=0, validation_data=(X_test,y_test)) |
Al final de la capacitación, evaluaremos el rendimiento del modelo en el conjunto de datos de prueba e informaremos el rendimiento como la precisión de la clasificación.
|
... # predecir el conjunto de pruebas yhat = modelo.predecir_clases(X_test) # evaluar predicciones puntaje = puntuación_de_precisión(y_test, yhat) imprimir(‘Precisión:% .3f’ % puntaje) |
Finalmente, trazaremos las curvas de aprendizaje de la pérdida de entropía cruzada en el tren y los conjuntos de prueba durante el entrenamiento.
|
... # trazar curvas de aprendizaje pyplot.título(‘Curvas de aprendizaje’) pyplot.xlabel(‘Época’) pyplot.etiquetarse(‘Entropía cruzada’) pyplot.trama(historia.historia[[‘pérdida’], etiqueta=‘tren’) pyplot.trama(historia.historia[[‘val_loss’], etiqueta=‘val’) pyplot.leyenda() pyplot.show() |
Uniendo todo esto, el ejemplo completo de evaluación de nuestro primer MLP en el conjunto de datos de la ionosfera se enumera a continuación.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 dieciséis 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 |
# ajuste un modelo mlp simple en la ionosfera y revise las curvas de aprendizaje de pandas importar read_csv de sklearn.model_selection importar train_test_split de sklearn.preprocesamiento importar LabelEncoder de sklearn.métrica importar puntuación_de_precisión de tensorflow.keras importar Secuencial de tensorflow.keras.capas importar Denso de matplotlib importar pyplot # cargar el conjunto de datos camino = ‘https://raw.githubusercontent.com/jbrownlee/Datasets/master/ionosphere.csv’ df = read_csv(camino, encabezamiento=Ninguno) # dividir en columnas de entrada y salida X, y = df.valores[[:, :–1], df.valores[[:, –1] # asegúrese de que todos los datos sean valores de punto flotante X = X.astipo(‘float32’) # codificar cadenas a números enteros y = LabelEncoder().fit_transform(y) # dividir en conjuntos de datos de prueba y de tren X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0,33) # determinar el número de características de entrada n_features = X.forma[[1] # definir modelo modelo = Secuencial() modelo.agregar(Denso(10, activación=‘relu’, kernel_initializer=‘él_normal’, input_shape=(n_features,))) modelo.agregar(Denso(1, activación=‘sigmoideo’)) # compilar el modelo modelo.compilar(optimizador=‘Adán’, pérdida=‘binary_crossentropy’) # se ajusta al modelo historia = modelo.encajar(X_train, y_train, épocas=200, tamaño del lote=32, verboso=0, validation_data=(X_test,y_test)) # predecir el conjunto de pruebas yhat = modelo.predecir_clases(X_test) # evaluar predicciones puntaje = precisión_puntaje(y_test, yhat) imprimir(‘Precisión:% .3f’ % puntaje) # trazar curvas de aprendizaje pyplot.título(‘Curvas de aprendizaje’) pyplot.xlabel(‘Época’) pyplot.etiquetarse(‘Entropía cruzada’) pyplot.trama(historia.historia[[‘pérdida’], etiqueta=‘tren’) pyplot.trama(historia.historia[[‘val_loss’], etiqueta=‘val’) pyplot.leyenda() pyplot.show() |
Ejecutar el ejemplo primero ajusta el modelo en el conjunto de datos de entrenamiento, luego informa la precisión de la clasificación en el conjunto de datos de prueba.
Nota: Sus resultados pueden variar dada la naturaleza estocástica del algoritmo o procedimiento de evaluación, o las diferencias en la precisión numérica. Considere ejecutar el ejemplo varias veces y compare el resultado promedio.
En este caso, podemos ver que el modelo logró una precisión de alrededor del 88 por ciento, que es una buena línea de base en el rendimiento que podríamos mejorar.
A continuación, se crean gráficos de líneas de la pérdida en el tren y los conjuntos de prueba.
Podemos ver que el modelo parece converger pero se ha sobreajustado al conjunto de datos de entrenamiento.
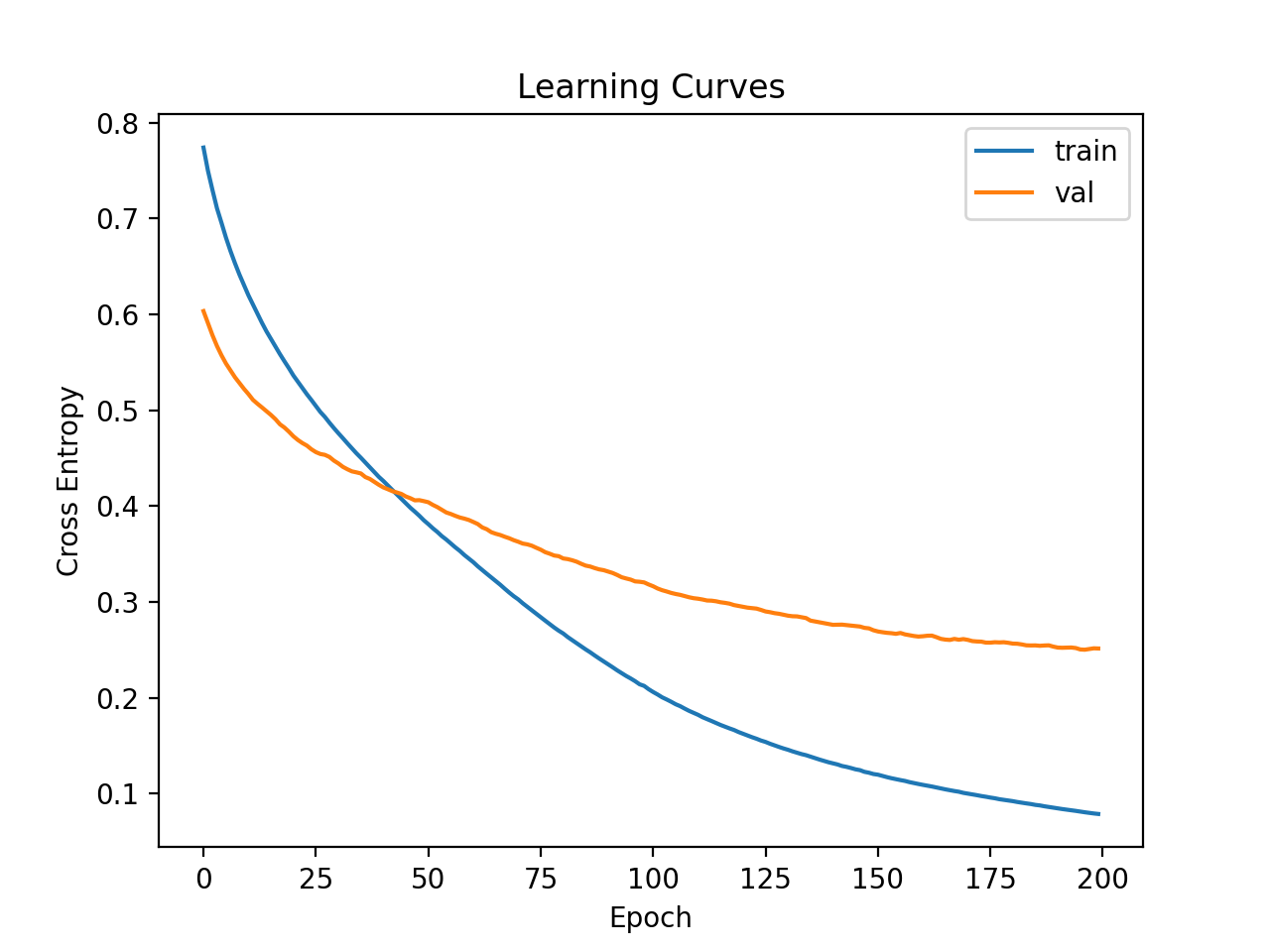
Curvas de aprendizaje de MLP simple en un conjunto de datos de ionosfera
Intentemos aumentar la capacidad del modelo.
Esto ralentizará el aprendizaje para los mismos hiperparámetros de aprendizaje y puede ofrecer una mayor precisión.
Agregaremos una segunda capa oculta con ocho nodos, elegidos arbitrariamente.
|
... # definir modelo modelo = Secuencial() modelo.agregar(Denso(10, activación=‘relu’, kernel_initializer=‘él_normal’, input_shape=(n_features,))) modelo.agregar(Denso(8, activación=‘relu’, kernel_initializer=‘él_normal’)) modelo.agregar(Denso(1, activación=‘sigmoideo’)) |
El ejemplo completo se enumera a continuación.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 dieciséis 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 |
# ajustar un modelo mlp más profundo en la ionosfera y revisar las curvas de aprendizaje de pandas importar read_csv de sklearn.model_selection importar train_test_split de sklearn.preprocesamiento importar LabelEncoder de sklearn.métrica importar precisión_puntaje de tensorflow.keras importar Secuencial de tensorflow.keras.capas importar Denso de matplotlib importar pyplot # cargar el conjunto de datos camino = ‘https://raw.githubusercontent.com/jbrownlee/Datasets/master/ionosphere.csv’ df = read_csv(camino, encabezamiento=Ninguno) # dividir en columnas de entrada y salida X, y = df.valores[[:, :–1], df.valores[[:, –1] # asegúrese de que todos los datos sean valores de punto flotante X = X.astipo(‘float32’) # codificar cadenas a números enteros y = LabelEncoder().fit_transform(y) # dividir en conjuntos de datos de prueba y de tren X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0,33) # determinar el número de características de entrada n_features = X.forma[[1] # definir modelo modelo = Secuencial() modelo.agregar(Denso(10, activación=‘relu’, kernel_initializer=‘él_normal’, input_shape=(n_features,))) modelo.agregar(Denso(8, activación=‘relu’, kernel_initializer=‘él_normal’)) modelo.agregar(Denso(1, activación=‘sigmoideo’)) # compilar el modelo modelo.compilar(optimizador=‘Adán’, pérdida=‘binary_crossentropy’) # se ajusta al modelo historia = modelo.encajar(X_train, y_train, épocas=200, tamaño del lote=32, verboso=0, validation_data=(X_test,y_test)) # predecir el conjunto de pruebas yhat = modelo.predecir_clases(X_test) # evaluar predicciones puntaje = puntuación_de_precisión(y_test, yhat) imprimir(‘Precisión:% .3f’ % puntaje) # trazar curvas de aprendizaje pyplot.título(‘Curvas de aprendizaje’) pyplot.xlabel(‘Época’) pyplot.etiquetarse(‘Entropía cruzada’) pyplot.trama(historia.historia[[‘pérdida’], etiqueta=‘tren’) pyplot.trama(historia.historia[[‘val_loss’], etiqueta=‘val’) pyplot.leyenda() |
Ejecutar el ejemplo primero ajusta el modelo en el conjunto de datos de entrenamiento, luego informa la precisión en el conjunto de datos de prueba.
Nota: Sus resultados pueden variar dada la naturaleza estocástica del algoritmo o procedimiento de evaluación, o diferencias en la precisión numérica. Considere ejecutar el ejemplo varias veces y compare el resultado promedio.
En este caso, podemos ver una ligera mejora en la precisión de alrededor del 93 por ciento, aunque la alta variación de la división tren / prueba significa que esta evaluación no es confiable.
Luego se trazan las curvas de aprendizaje para la pérdida en el tren y los conjuntos de prueba. Podemos ver que el modelo todavía parece mostrar un comportamiento de sobreajuste.
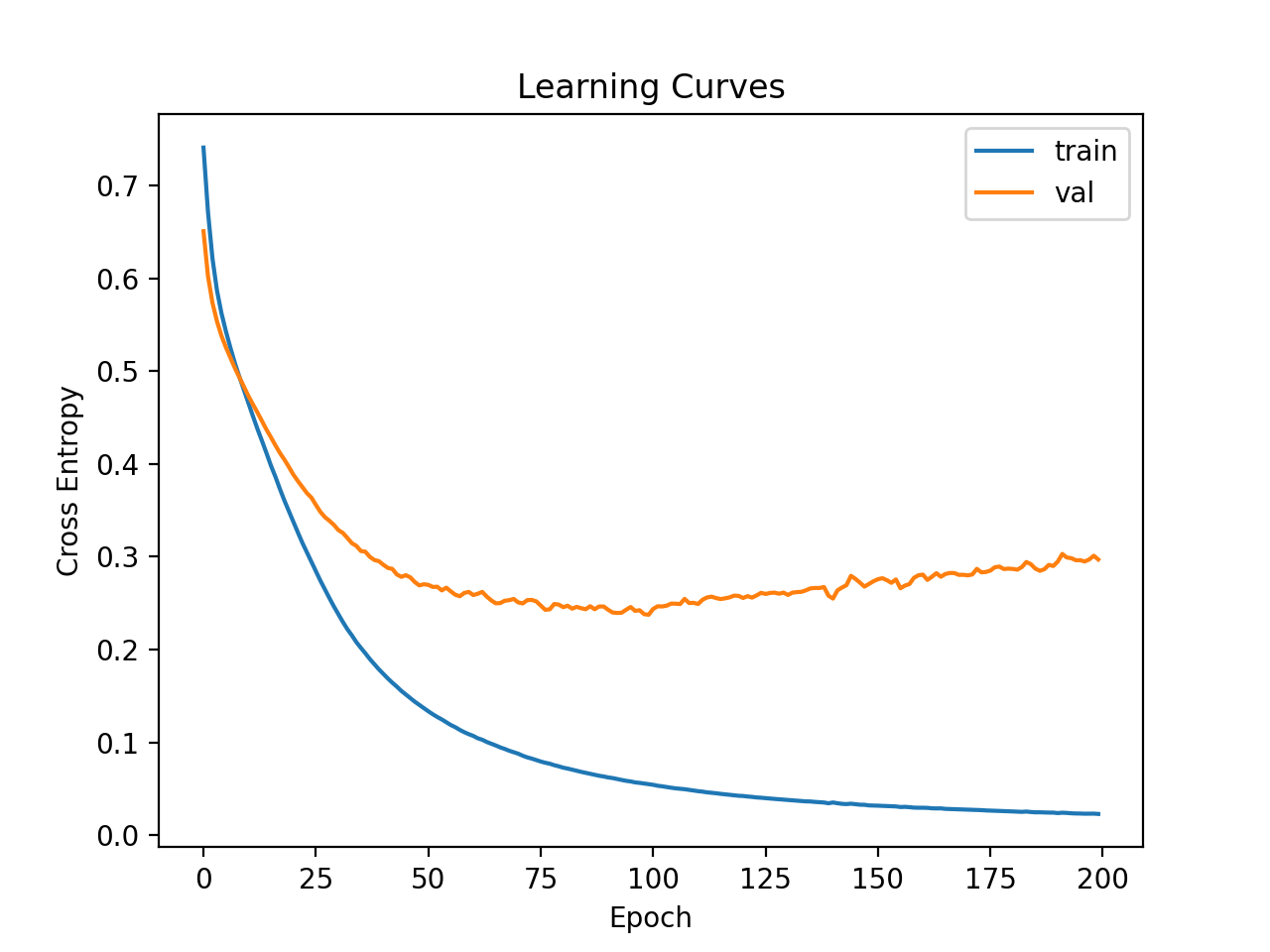
Curvas de aprendizaje de MLP más profundo en el conjunto de datos de la ionosfera
Finally, we can try a wider network.
We will increase the number of nodes in the first hidden layer from 10 to 50, and in the second hidden layer from 8 to 10.
This will add more capacity to the model, slow down learning, and may further improve results.
|
... # define model modelo = Sequential() modelo.add(Dense(50, activation=‘relu’, kernel_initializer=‘he_normal’, input_shape=(n_features,))) modelo.add(Dense(10, activation=‘relu’, kernel_initializer=‘he_normal’)) modelo.add(Dense(1, activation=‘sigmoid’)) |
We will also reduce the number of training epochs from 200 to 100.
|
... # fit the model history = modelo.fit(X_train, y_train, epochs=100, batch_size=32, verbose=0, validation_data=(X_test,y_test)) |
The complete example is listed below.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 dieciséis 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 |
# fit a wider mlp model on the ionosphere and review learning curves de pandas import read_csv de sklearn.model_selection import train_test_split de sklearn.preprocessing import LabelEncoder de sklearn.metrics import accuracy_score de tensorflow.keras import Sequential de tensorflow.keras.layers import Dense de matplotlib import pyplot # load the dataset path = ‘https://raw.githubusercontent.com/jbrownlee/Datasets/master/ionosphere.csv’ df = read_csv(path, header=None) # split into input and output columns X, y = df.values[[:, :–1], df.values[[:, –1] # ensure all data are floating point values X = X.astype(‘float32’) # encode strings to integer y = LabelEncoder().fit_transform(y) # split into train and test datasets X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.33) # determine the number of input features n_features = X.shape[[1] # define model modelo = Sequential() modelo.add(Dense(50, activation=‘relu’, kernel_initializer=‘he_normal’, input_shape=(n_features,))) modelo.add(Dense(10, activation=‘relu’, kernel_initializer=‘he_normal’)) modelo.add(Dense(1, activation=‘sigmoid’)) # compile the model modelo.compile(optimizer=‘adam’, loss=‘binary_crossentropy’) # fit the model history = modelo.fit(X_train, y_train, epochs=100, batch_size=32, verbose=0, validation_data=(X_test,y_test)) # predict test set yhat = modelo.predict_classes(X_test) # evaluate predictions score = accuracy_score(y_test, yhat) imprimir(‘Accuracy: %.3f’ % score) # plot learning curves pyplot.title(‘Learning Curves’) pyplot.xlabel(‘Epoch’) pyplot.ylabel(‘Cross Entropy’) pyplot.plot(history.history[[‘loss’], label=‘train’) pyplot.plot(history.history[[‘val_loss’], label=‘val’) pyplot.legend() pyplot.show() |
Running the example first fits the model on the training dataset, then reports the accuracy on the test dataset.
Nota: Your results may vary given the stochastic nature of the algorithm or evaluation procedure, or differences in numerical precision. Consider running the example a few times and compare the average outcome.
In this case, the model achieves a better accuracy score, with a value of about 94 percent. We will ignore model performance for now.
Line plots of the learning curves are created showing that the model achieved a reasonable fit and had more than enough time to converge.

Learning Curves of Wider MLP on the Ionosphere Dataset
Now that we have some idea of the learning dynamics for simple MLP models on the dataset, we can look at evaluating the performance of the models as well as tuning the configuration of the models.
Evaluating and Tuning MLP Models
The k-fold cross-validation procedure can provide a more reliable estimate of MLP performance, although it can be very slow.
This is because k models must be fit and evaluated. This is not a problem when the dataset size is small, such as the ionosphere dataset.
We can use the StratifiedKFold class and enumerate each fold manually, fit the model, evaluate it, and then report the mean of the evaluation scores at the end of the procedure.
|
# prepare cross validation kfold = KFold(10) # enumerate splits scores = lista() para train_ix, test_ix in kfold.split(X, y): # fit and evaluate the model… ... ... # summarize all scores imprimir(‘Mean Accuracy: %.3f (%.3f)’ % (mean(scores), std(scores))) |
We can use this framework to develop a reliable estimate of MLP model performance with a range of different data preparations, model architectures, and learning configurations.
It is important that we first developed an understanding of the learning dynamics of the model on the dataset in the previous section before using k-fold cross-validation to estimate the performance. If we started to tune the model directly, we might get good results, but if not, we might have no idea of why, e.g. that the model was over or under fitting.
If we make large changes to the model again, it is a good idea to go back and confirm that the model is converging appropriately.
The complete example of this framework to evaluate the base MLP model from the previous section is listed below.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 dieciséis 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 |
# k-fold cross-validation of base model for the ionosphere dataset de numpy import mean de numpy import std de pandas import read_csv de sklearn.model_selection import StratifiedKFold de sklearn.preprocessing import LabelEncoder de sklearn.metrics import accuracy_score de tensorflow.keras import Sequential de tensorflow.keras.layers import Dense de matplotlib import pyplot # load the dataset path = ‘https://raw.githubusercontent.com/jbrownlee/Datasets/master/ionosphere.csv’ df = read_csv(path, header=None) # split into input and output columns X, y = df.values[[:, :–1], df.values[[:, –1] # ensure all data are floating point values X = X.astype(‘float32’) # encode strings to integer y = LabelEncoder().fit_transform(y) # prepare cross validation kfold = StratifiedKFold(10) # enumerate splits scores = lista() para train_ix, test_ix in kfold.split(X, y): # split data X_train, X_test, y_train, y_test = X[[train_ix], X[[test_ix], y[[train_ix], y[[test_ix] # determine the number of input features n_features = X.shape[[1] # define model modelo = Sequential() modelo.add(Dense(50, activation=‘relu’, kernel_initializer=‘he_normal’, input_shape=(n_features,))) modelo.add(Dense(10, activation=‘relu’, kernel_initializer=‘he_normal’)) modelo.add(Dense(1, activation=‘sigmoid’)) # compile the model modelo.compile(optimizer=‘adam’, loss=‘binary_crossentropy’) # fit the model modelo.fit(X_train, y_train, epochs=100, batch_size=32, verbose=0) # predict test set yhat = modelo.predict_classes(X_test) # evaluate predictions score = accuracy_score(y_test, yhat) imprimir(‘>%.3f’ % score) scores.adjuntar(score) # summarize all scores imprimir(‘Mean Accuracy: %.3f (%.3f)’ % (mean(scores), std(scores))) |
Running the example reports the model performance each iteration of the evaluation procedure and reports the mean and standard deviation of classification accuracy at the end of the run.
Nota: Your results may vary given the stochastic nature of the algorithm or evaluation procedure, or differences in numerical precision. Consider running the example a few times and compare the average outcome.
In this case, we can see that the MLP model achieved a mean accuracy of about 93.4 percent.
We will use this result as our baseline to see if we can achieve better performance.
|
>0.972 >0.886 >0.943 >0.886 >0.914 >0.943 >0.943 >1.000 >0.971 >0.886 Mean Accuracy: 0.934 (0.039) |
Next, let’s try adding regularization to reduce overfitting of the model.
In this case, we can add dropout layers between the hidden layers of the network. For example:
|
... # define model modelo = Sequential() modelo.add(Dense(50, activation=‘relu’, kernel_initializer=‘he_normal’, input_shape=(n_features,))) modelo.add(Dropout(0.4)) modelo.add(Dense(10, activation=‘relu’, kernel_initializer=‘he_normal’)) modelo.add(Dropout(0.4)) modelo.add(Dense(1, activation=‘sigmoid’)) |
The complete example of the MLP model with dropout is listed below.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 dieciséis 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 |
# k-fold cross-validation of the MLP with dropout for the ionosphere dataset de numpy import mean de numpy import std de pandas import read_csv de sklearn.model_selection import StratifiedKFold de sklearn.preprocessing import LabelEncoder de sklearn.metrics import accuracy_score de tensorflow.keras import Sequential de tensorflow.keras.layers import Dense de tensorflow.keras.layers import Dropout de matplotlib import pyplot # load the dataset path = ‘https://raw.githubusercontent.com/jbrownlee/Datasets/master/ionosphere.csv’ df = read_csv(path, header=None) # split into input and output columns X, y = df.values[[:, :–1], df.values[[:, –1] # ensure all data are floating point values X = X.astype(‘float32’) # encode strings to integer y = LabelEncoder().fit_transform(y) # prepare cross validation kfold = StratifiedKFold(10) # enumerate splits scores = lista() para train_ix, test_ix in kfold.split(X, y): # split data X_train, X_test, y_train, y_test = X[[train_ix], X[[test_ix], y[[train_ix], y[[test_ix] # determine the number of input features n_features = X.shape[[1] # define model modelo = Sequential() modelo.add(Dense(50, activation=‘relu’, kernel_initializer=‘he_normal’, input_shape=(n_features,))) modelo.add(Dropout(0.4)) modelo.add(Dense(10, activation=‘relu’, kernel_initializer=‘he_normal’)) modelo.add(Dropout(0.4)) modelo.add(Dense(1, activation=‘sigmoid’)) # compile the model modelo.compile(optimizer=‘adam’, loss=‘binary_crossentropy’) # fit the model modelo.fit(X_train, y_train, epochs=100, batch_size=32, verbose=0) # predict test set yhat = modelo.predict_classes(X_test) # evaluate predictions score = accuracy_score(y_test, yhat) imprimir(‘>%.3f’ % score) scores.adjuntar(score) # summarize all scores imprimir(‘Mean Accuracy: %.3f (%.3f)’ % (mean(scores), std(scores))) |
Running reports the mean and standard deviation of the classification accuracy at the end of the run.
Nota: Your results may vary given the stochastic nature of the algorithm or evaluation procedure, or differences in numerical precision. Consider running the example a few times and compare the average outcome.
In this case, we can see that the MLP model with dropout achieves better results with an accuracy of about 94.6 percent compared to 93.4 percent without dropout
|
Mean Accuracy: 0.946 (0.043) |
Finally, we will try reducing the batch size from 32 down to 8.
This will result in more noisy gradients and may also slow down the speed at which the model is learning the problem.
|
... # fit the model modelo.fit(X_train, y_train, epochs=100, batch_size=8, verbose=0) |
The complete example is listed below.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 dieciséis 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 |
# k-fold cross-validation of the MLP with dropout for the ionosphere dataset de numpy import mean de numpy import std de pandas import read_csv de sklearn.model_selection import StratifiedKFold de sklearn.preprocessing import LabelEncoder de sklearn.metrics import accuracy_score de tensorflow.keras import Sequential de tensorflow.keras.layers import Dense de tensorflow.keras.layers import Dropout de matplotlib import pyplot # load the dataset path = ‘https://raw.githubusercontent.com/jbrownlee/Datasets/master/ionosphere.csv’ df = read_csv(path, header=None) # split into input and output columns X, y = df.values[[:, :–1], df.values[[:, –1] # ensure all data are floating point values X = X.astype(‘float32’) # encode strings to integer y = LabelEncoder().fit_transform(y) # prepare cross validation kfold = StratifiedKFold(10) # enumerate splits scores = lista() para train_ix, test_ix in kfold.split(X, y): # split data X_train, X_test, y_train, y_test = X[[train_ix], X[[test_ix], y[[train_ix], y[[test_ix] # determine the number of input features n_features = X.shape[[1] # define model modelo = Sequential() modelo.add(Dense(50, activation=‘relu’, kernel_initializer=‘he_normal’, input_shape=(n_features,))) modelo.add(Dropout(0.4)) modelo.add(Dense(10, activation=‘relu’, kernel_initializer=‘he_normal’)) modelo.add(Dropout(0.4)) modelo.add(Dense(1, activation=‘sigmoid’)) # compile the model modelo.compile(optimizer=‘adam’, loss=‘binary_crossentropy’) # fit the model modelo.fit(X_train, y_train, epochs=100, batch_size=8, verbose=0) # predict test set yhat = modelo.predict_classes(X_test) # evaluate predictions score = accuracy_score(y_test, yhat) imprimir(‘>%.3f’ % score) scores.adjuntar(score) # summarize all scores imprimir(‘Mean Accuracy: %.3f (%.3f)’ % (mean(scores), std(scores))) |
Running reports the mean and standard deviation of the classification accuracy at the end of the run.
Nota: Your results may vary given the stochastic nature of the algorithm or evaluation procedure, or differences in numerical precision. Consider running the example a few times and compare the average outcome.
In this case, we can see that the MLP model with dropout achieves slightly better results with an accuracy of about 94.9 percent.
|
Mean Accuracy: 0.949 (0.042) |
We will use this configuration as our final model.
We could continue to test alternate configurations to the model architecture (more or fewer nodes or layers), learning hyperparameters (more or fewer batches), and data transforms.
I leave this as an exercise; let me know what you discover. Can you get better results?
Post your results in the comments below, I’d love to see what you get.
Next, let’s look at how we might fit a final model and use it to make predictions.
Final Model and Make Predictions
Once we choose a model configuration, we can train a final model on all available data and use it to make predictions on new data.
In this case, we will use the model with dropout and a small batch size as our final model.
We can prepare the data and fit the model as before, although on the entire dataset instead of a training subset of the dataset.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 dieciséis 17 18 19 |
... # split into input and output columns X, y = df.values[[:, :–1], df.values[[:, –1] # ensure all data are floating point values X = X.astype(‘float32’) # encode strings to integer le = LabelEncoder() y = le.fit_transform(y) # determine the number of input features n_features = X.shape[[1] # define model modelo = Sequential() modelo.add(Dense(50, activation=‘relu’, kernel_initializer=‘he_normal’, input_shape=(n_features,))) modelo.add(Dropout(0.4)) modelo.add(Dense(10, activation=‘relu’, kernel_initializer=‘he_normal’)) modelo.add(Dropout(0.4)) modelo.add(Dense(1, activation=‘sigmoid’)) # compile the model modelo.compile(optimizer=‘adam’, loss=‘binary_crossentropy’) |
We can then use this model to make predictions on new data.
First, we can define a row of new data.
|
... # define a row of new data row = [[1,0,0.99539,–0.05889,0.85243,0.02306,0.83398,–0.37708,1,0.03760,0.85243,–0.17755,0.59755,–0.44945,0.60536,–0.38223,0.84356,–0.38542,0.58212,–0.32192,0.56971,–0.29674,0.36946,–0.47357,0.56811,–0.51171,0.41078,–0.46168,0.21266,–0.34090,0.42267,–0.54487,0.18641,–0.45300] |
Note: I took this row from the first row of the dataset and the expected label is a ‘gramo‘.
We can then make a prediction.
|
... # make prediction yhat = modelo.predict_classes([[row]) |
Then invert the transform on the prediction, so we can use or interpret the result in the correct label.
|
... # invert transform to get label for class yhat = le.inverse_transform(yhat) |
And in this case, we will simply report the prediction.
|
... # report prediction imprimir(‘Predicted: %s’ % (yhat[[0])) |
Tying this all together, the complete example of fitting a final model for the ionosphere dataset and using it to make a prediction on new data is listed below.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 dieciséis 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 |
# fit a final model and make predictions on new data for the ionosphere dataset de pandas import read_csv de sklearn.preprocessing import LabelEncoder de sklearn.metrics import accuracy_score de tensorflow.keras import Sequential de tensorflow.keras.layers import Dense de tensorflow.keras.layers import Dropout # load the dataset path = ‘https://raw.githubusercontent.com/jbrownlee/Datasets/master/ionosphere.csv’ df = read_csv(path, header=None) # split into input and output columns X, y = df.values[[:, :–1], df.values[[:, –1] # ensure all data are floating point values X = X.astype(‘float32’) # encode strings to integer le = LabelEncoder() y = le.fit_transform(y) # determine the number of input features n_features = X.shape[[1] # define model modelo = Sequential() modelo.add(Dense(50, activation=‘relu’, kernel_initializer=‘he_normal’, input_shape=(n_features,))) modelo.add(Dropout(0.4)) modelo.add(Dense(10, activation=‘relu’, kernel_initializer=‘he_normal’)) modelo.add(Dropout(0.4)) modelo.add(Dense(1, activation=‘sigmoid’)) # compile the model modelo.compile(optimizer=‘adam’, loss=‘binary_crossentropy’) # fit the model modelo.fit(X, y, epochs=100, batch_size=8, verbose=0) # define a row of new data row = [[1,0,0.99539,–0.05889,0.85243,0.02306,0.83398,–0.37708,1,0.03760,0.85243,–0.17755,0.59755,–0.44945,0.60536,–0.38223,0.84356,–0.38542,0.58212,–0.32192,0.56971,–0.29674,0.36946,–0.47357,0.56811,–0.51171,0.41078,–0.46168,0.21266,–0.34090,0.42267,–0.54487,0.18641,–0.45300] # make prediction yhat = modelo.predict_classes([[row]) # invert transform to get label for class yhat = le.inverse_transform(yhat) # report prediction imprimir(‘Predicted: %s’ % (yhat[[0])) |
Running the example fits the model on the entire dataset and makes a prediction for a single row of new data.
Nota: Your results may vary given the stochastic nature of the algorithm or evaluation procedure, or differences in numerical precision. Consider running the example a few times and compare the average outcome.
In this case, we can see that the model predicted a “g” label for the input row.
Further Reading
This section provides more resources on the topic if you are looking to go deeper.
Tutorials
Summary
In this tutorial, you discovered how to develop a Multilayer Perceptron neural network model for the ionosphere binary classification dataset.
Specifically, you learned:
- How to load and summarize the ionosphere dataset and use the results to suggest data preparations and model configurations to use.
- How to explore the learning dynamics of simple MLP models on the dataset.
- How to develop robust estimates of model performance, tune model performance and make predictions on new data.
Do you have any questions?
Ask your questions in the comments below and I will do my best to answer.

