
Este artículo es parte de nuestras revisiones de artículos de investigación de IA, una serie de publicaciones que exploran los últimos hallazgos en inteligencia artificial.
El aprendizaje profundo puede ayudar a descubrir relaciones matemáticas que evaden a los científicos humanos, según muestra un artículo reciente de investigadores de DeepMind. Como muchas cosas provenientes del laboratorio de inteligencia artificial propiedad de Alphabet, el artículo, que se titula «Avanzar en las matemáticas guiando la intuición humana con IA», ha recibido mucha atención de los medios científicos y tecnológicos.
Algunos matemáticos e informáticos han elogiado los esfuerzos de DeepMind y los hallazgos del artículo como avances. Otros son más escépticos y creen que el uso del aprendizaje profundo en matemáticas podría haber sido exagerado en el artículo y su cobertura en la prensa popular.
No obstante, los resultados son fascinantes y pueden ampliar la caja de herramientas de los científicos para descubrir y probar teoremas matemáticos.
Un marco para el descubrimiento matemático con aprendizaje automático
En su artículo, los científicos de DeepMind sugieren que la IA se puede utilizar para «ayudar en el descubrimiento de teoremas y conjeturas en la vanguardia de la investigación matemática». Proponen un «marco para aumentar el conjunto de herramientas del matemático estándar con potentes métodos de reconocimiento e interpretación de patrones a partir del aprendizaje automático».
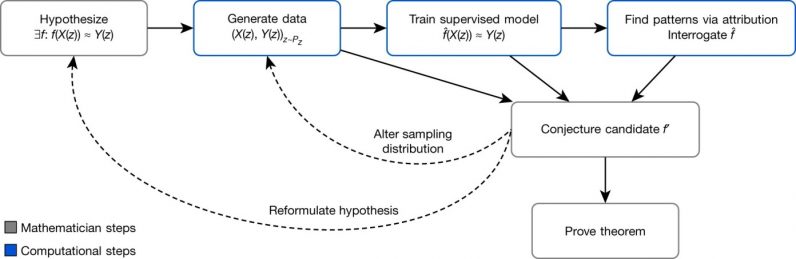
Los matemáticos comienzan haciendo una hipótesis sobre la relación entre dos objetos matemáticos. Para verificar la hipótesis, utilizan programas de computadora para generar datos para ambos tipos de objetos. A continuación, un algoritmo de modelo de aprendizaje automático supervisado procesa los números e intenta ajustar sus parámetros que asignan un tipo de objeto al otro.
«Las contribuciones clave del aprendizaje automático en este proceso de regresión son el amplio conjunto de posibles funciones no lineales que se pueden aprender con una cantidad suficiente de datos», escriben los investigadores.
Si el modelo entrenado funciona mejor que la adivinación aleatoria, entonces podría indicar que efectivamente existe una relación detectable entre los dos objetos matemáticos. Usando varias técnicas de aprendizaje automático, los investigadores pueden encontrar los puntos de datos que son más relevantes para el problema, reformar su hipótesis, generar nuevos datos y entrenar nuevos modelos. Al repetir estos pasos, pueden reducir el conjunto de conjeturas plausibles y acelerar su camino hacia una solución final.
Los científicos de DeepMind describen el marco como un «banco de pruebas para la intuición» que puede verificar rápidamente «si vale la pena seguir una intuición sobre la relación entre dos cantidades» y proporcionar orientación sobre cómo pueden estar relacionadas.
Usando este marco, los investigadores de DeepMind utilizaron el aprendizaje profundo para alcanzar «dos nuevos descubrimientos fundamentales, uno en topología y otro en teoría de representación».
Un aspecto interesante del trabajo fue que no requirió la enorme cantidad de poder de cómputo que se ha convertido en un pilar de la investigación de DeepMind. Según el documento, los modelos de aprendizaje profundo utilizados en ambos descubrimientos se pueden entrenar «en varias horas en una máquina con una sola unidad de procesamiento de gráficos».
Nudos y representaciones
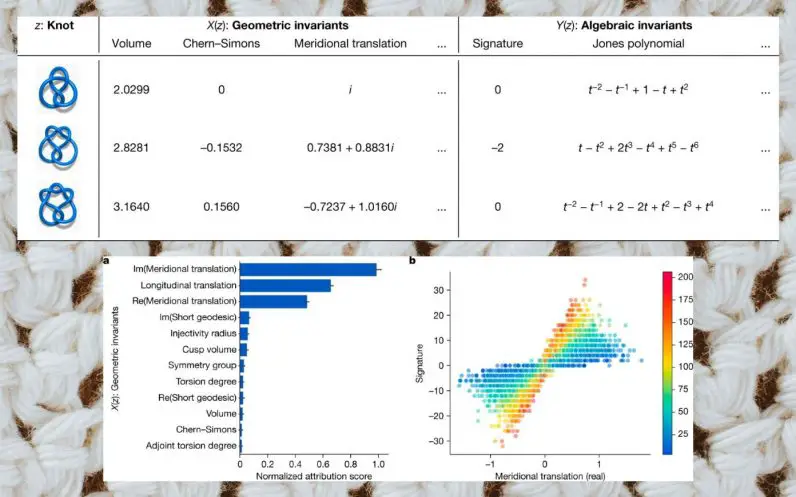
Los nudos son bucles cerrados en el espacio dimensional que se pueden definir de varias formas. Se vuelven más complejos a medida que aumenta el número de sus cruces. Los investigadores querían ver si podían usar el aprendizaje automático para descubrir un mapeo entre invariantes algebraicos e invariantes hiperbólicos, dos formas fundamentalmente diferentes de definir nudos.
«Nuestra hipótesis era que existe una relación no descubierta entre los invariantes hiperbólicos y algebraicos de un nudo», escriben los investigadores.
Usando el paquete de software SnapPy, los investigadores generaron la «firma», un invariante algebraico y 12 invariantes hiperbólicos prometedores para 1,7 millones de nudos con hasta 16 cruces.
A continuación, crearon una red neuronal de retroalimentación totalmente conectada con tres capas ocultas, cada una con 300 unidades. Entrenaron el modelo de aprendizaje profundo para mapear los valores de las invariantes hiperbólicas a la firma. Su modelo inicial fue capaz de predecir la firma con un 78 por ciento de precisión. Un análisis más detallado los llevó a un conjunto más pequeño de parámetros en las invariantes hiperbólicas que eran predictivas de la firma. Los investigadores refinaron su conjetura, generaron nuevos datos, volvieron a entrenar sus modelos y llegaron a un teorema final.
Los investigadores describen el teorema como «uno de los primeros resultados que conectan los invariantes algebraicos y geométricos de los nudos y tiene varias aplicaciones interesantes».
“Esperamos que esta relación recién descubierta entre la pendiente natural y la firma tenga muchas otras aplicaciones en topología de baja dimensión. Es sorprendente que una conexión simple pero profunda como esta se haya pasado por alto en un área que ha sido ampliamente estudiada ”, escriben los investigadores.
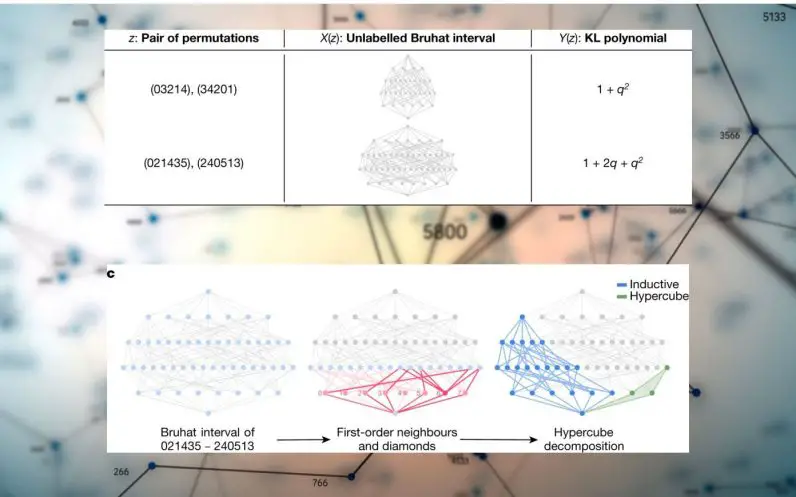
El segundo resultado del artículo es también un mapeo de dos visiones diferentes de simetrías, un problema que es mucho más complicado que los nudos.
En este caso, utilizaron un tipo de red neuronal gráfica (GNN) para encontrar relaciones entre el gráfico de intervalo de Bruhat y el polinomio Kazhdan-Lusztig (KL). Uno de los beneficios de los GNN es que pueden calcular y aprender gráficos que son muy grandes y difíciles de administrar para la mente sin ayuda. El modelo de aprendizaje profundo toma el gráfico de intervalo como entrada e intenta predecir el polinomio KL correspondiente.
Nuevamente, al generar datos, entrenar modelos DL y reajustar el proceso, los científicos pudieron formular una conjetura demostrable.
Reacciones a la inteligencia artificial matemática de DeepMind
Hablando sobre el descubrimiento de DeepMind en la teoría de nudos, Mark Brittenham, un teórico de nudos de la Universidad de Nebraska – Lincoln dijo Naturaleza, “El hecho de que los autores hayan probado que estos invariantes están relacionados, y de una manera notablemente directa, nos muestra que hay algo muy fundamental que nosotros en el campo aún tenemos que entender completamente”. Brittenham agregó que, en comparación con otros esfuerzos para aplicar el aprendizaje automático a los nudos, la técnica de DeepMind es novedosa en su capacidad para descubrir conexiones sorprendentes.
Adam Zsolt Wagner, matemático de la Universidad de Tel Aviv, Israel, que también habló con Nature, dijo que los métodos presentados por DeepMind podrían resultar valiosos para ciertos tipos de problemas.
Wagner, que tiene experiencia en la aplicación del aprendizaje automático a las matemáticas, dijo: «Sin esta herramienta, el matemático podría perder semanas o meses tratando de probar una fórmula o teorema que, en última instancia, resultaría falso». Pero también agregó que no está claro qué tan amplio será su impacto.
Razones para ser escéptico

Tras la publicación del trabajo de DeepMind en Nature, Ernest Davis, profesor de Ciencias de la Computación en la Universidad de Nueva York, publicó un artículo propio, que plantea algunas preguntas importantes sobre el encuadre de DeepMind de los resultados y los límites de la aplicación del aprendizaje profundo a las matemáticas en general.
En el primer resultado presentado en el artículo de DeepMind, Davis observa que la teoría del nudo no es el tipo de problema en el que el aprendizaje profundo suele eclipsar a otros métodos estadísticos o de aprendizaje automático.
“La fortaleza de DL está en casos como visión o texto donde cada instancia (imagen o texto) tiene una gran cantidad de características de entrada de bajo nivel, es difícil identificar de manera confiable las características de alto nivel y la función que relaciona las características de entrada con la respuesta es, por lo que cualquiera puede decir, inmensamente complejo, con un subconjunto no pequeño de las características de entrada que son determinantes ”, escribe Davis.
El problema del nudo tenía solo doce características de entrada, de las cuales solo tres resultaron ser relevantes. Y la relación matemática entre las características de entrada y la variable objetivo era simple.
“Es difícil ver por qué una red neuronal con 200.000 parámetros sería el método de elección; Los métodos estadísticos simples y convencionales o una máquina de vectores de soporte serían más adecuados ”, escribe Davis.
En el segundo proyecto, el papel del aprendizaje profundo fue mucho más relevante, señala Davis. “A diferencia del proyecto de la teoría del nudo, que utilizó una arquitectura DL genérica, la red neuronal se diseñó cuidadosamente para adaptarse a un conocimiento matemático profundo sobre el problema. Además, el DL funcionó mucho mejor, con algo así como 1/40 de la tasa de error, en datos preprocesados que en los datos originales ”, escribe.
Por un lado, los resultados contrastan con las críticas relativas a que es difícil incorporar el conocimiento del dominio en el aprendizaje profundo, señala Davis. “Por otro lado, los entusiastas de la DL a menudo han elogiado la DL como una metodología de aprendizaje ‘plug-and-play’ que se puede utilizar con datos sin procesar para cualquier problema que se presente; esto va en contra de ese elogio ”, escribe.
Davis también señala que el éxito de aplicar el aprendizaje profundo a estas tareas puede depender fundamentalmente de la forma en que se generan los datos de entrenamiento y la forma en que se codifican las estructuras matemáticas. Esto sugiere que el marco podría aplicarse a una clase limitada de problemas matemáticos.
“Encontrar la mejor manera de generar y codificar datos implica una mezcla de teoría, experiencia, arte y experimentación. La carga de todo esto recae en el experto humano ”, escribe. «El aprendizaje profundo puede ser una herramienta poderosa, pero no siempre es robusta».
Davis advierte que en el clima actual de exageración que rodea al aprendizaje profundo, «existe un incentivo perverso para enfocar el papel de la DL en esta investigación, no solo para los especialistas en ML de DeepMind, sino incluso para los matemáticos».
Davis concluye que, como se usa en el documento, el aprendizaje profundo se ve mejor como «otra herramienta analítica en la caja de herramientas de las matemáticas experimentales en lugar de como un enfoque fundamentalmente nuevo de las matemáticas».
Vale la pena señalar que los autores del artículo original también han señalado algunos de los límites de su marco, incluido que “requiere la capacidad de generar grandes conjuntos de datos de las representaciones de objetos y que los patrones sean detectables en ejemplos que son calculable. Además, en algunos dominios, las funciones de interés pueden ser difíciles de aprender en este paradigma «.
Aprendizaje profundo e intuición

Uno de los temas de controversia es la afirmación del artículo de que el aprendizaje profundo es «guiar la intuición». Davis describe esta afirmación como una «descripción seriamente inexacta de la ayuda que los matemáticos han obtenido, o pueden esperar obtener, de este uso de los sistemas DL».
La intuición es uno de los diferenciadores clave entre la inteligencia humana y la artificial. Es la capacidad de tomar decisiones que son mejores que las suposiciones aleatorias y pueden dirigirlo en la dirección correcta la mayor parte del tiempo. Como ha demostrado la historia de la IA hasta ahora, la intuición no se captura en innumerables reglas o patrones predefinidos que se encuentran en grandes cantidades de datos.
“En el contexto matemático, la palabra ‘intuitivo’ significa que un concepto o una prueba puede basarse en el sentido profundo de una persona de dominios familiares como la numerosidad, el espacio, el tiempo o el movimiento, o de alguna otra manera ‘tiene sentido ‘o’ parece correcto ‘de una manera que no implique un cálculo explícito o un razonamiento paso a paso ”, escribe Davis.
Si bien obtener una comprensión intuitiva de los conceptos matemáticos a menudo requiere trabajar con múltiples ejemplos específicos, no es un trabajo de correlaciones estadísticas, argumenta Davis. En otras palabras, no obtienes intuiciones ejecutando millones de ejemplos y observando el porcentaje de veces que se repiten ciertos patrones.
Esto significa que no fueron los modelos de aprendizaje profundo los que proporcionaron a los científicos una comprensión intuitiva de los conceptos que definieron, los teoremas que probaron y las conjeturas que plantearon.
Davis escribe: “Lo que hizo el DL fue darles algunos consejos sobre qué características del problema parecían ser importantes y cuáles no parecían importantes. Eso no es para estornudar, pero no debe exagerarse «.
Este artículo fue publicado originalmente por Ben Dickson en TechTalks, una publicación que examina las tendencias en tecnología, cómo afectan la forma en que vivimos y hacemos negocios, y los problemas que resuelven. Pero también discutimos el lado malo de la tecnología, las implicaciones más oscuras de la nueva tecnología y lo que debemos tener en cuenta. Puede leer el artículo original aquí.
