Cálculo en acción: redes neuronales

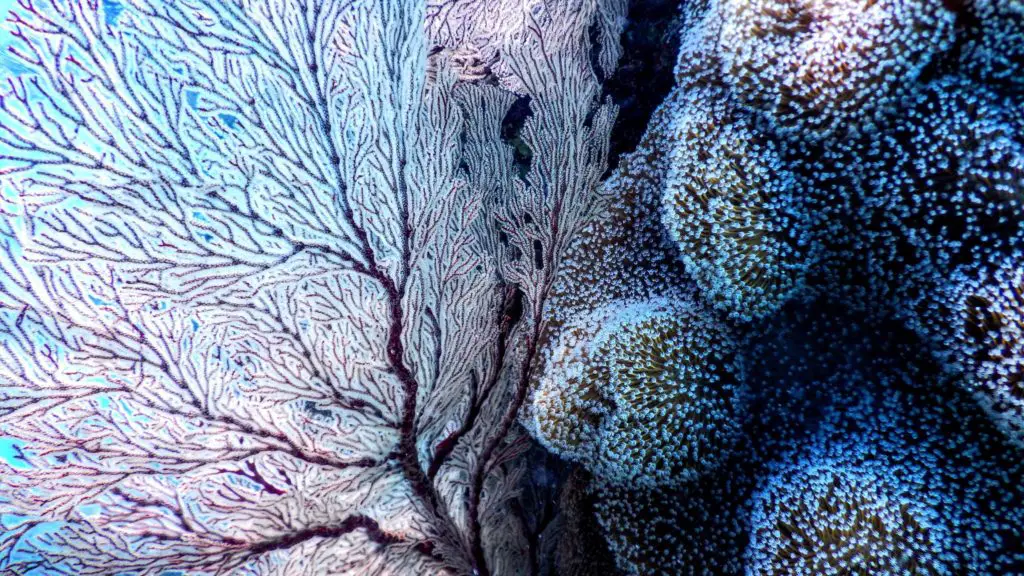
Una red neuronal artificial es un modelo computacional que se aproxima a un mapeo entre entradas y salidas.

Está inspirado en la estructura del cerebro humano, en el sentido de que está compuesto de manera similar por una red de neuronas interconectadas que propagan información al recibir conjuntos de estímulos de neuronas vecinas.

El entrenamiento de una red neuronal implica un proceso que emplea los algoritmos de retropropagación y descenso de gradiente en tándem. Como veremos, ambos algoritmos hacen un uso extensivo del cálculo.

En este tutorial, descubrirá cómo se aplican los aspectos del cálculo en las redes neuronales.

Después de completar este tutorial, sabrá:

• Una red neuronal artificial se organiza en capas de neuronas y conexiones, donde a estas últimas se les atribuye un valor ponderado a cada una.
• Cada neurona implementa una función no lineal que asigna un conjunto de entradas a una activación de salida.
• Al entrenar una red neuronal, los algoritmos de retropropagación y descenso de gradiente utilizan ampliamente el cálculo.

Empecemos.

Cálculo en acción: redes neuronales
Foto de Tomoe Steineck, algunos derechos reservados.

Descripción general del tutorial

Este tutorial se divide en tres partes; son:

• Introducción a la red neuronal
• Las matemáticas de una neurona
• Entrenando a la Red

Prerrequisitos

Para este tutorial, asumimos que ya sabe cuáles son:

Puede revisar estos conceptos haciendo clic en los enlaces que aparecen arriba.

Introducción a la red neuronal

Las redes neuronales artificiales se pueden considerar como algoritmos de aproximación de funciones.

En un entorno de aprendizaje supervisado, cuando se le presentan muchas observaciones de entrada que representan el problema de interés, junto con sus correspondientes salidas objetivo, la red neuronal artificial buscará aproximarse al mapeo que existe entre los dos.

Una red neuronal es un modelo computacional que se inspira en la estructura del cerebro humano.

– Página 65, Deep Learning, 2019.

El cerebro humano consta de una red masiva de neuronas interconectadas (alrededor de cien mil millones de ellas), cada una de las cuales comprende un cuerpo celular, un conjunto de fibras llamadas dendritas y un axón:

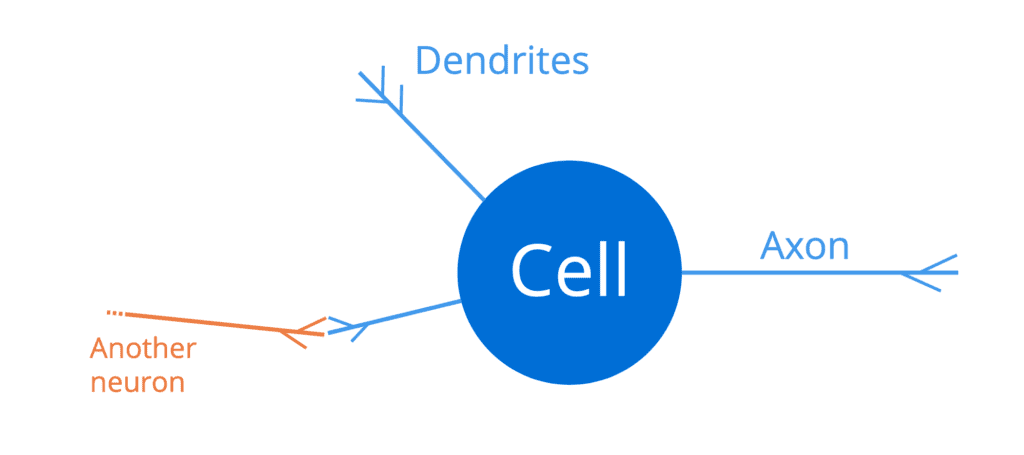
Una neurona en el cerebro humano

Las dendritas actúan como canales de entrada a una neurona, mientras que el axón actúa como canal de salida. Por lo tanto, una neurona recibiría señales de entrada a través de sus dendritas, que a su vez estarían conectadas a los axones (de salida) de otras neuronas vecinas. De esta manera, se puede transmitir un pulso eléctrico suficientemente fuerte (también llamado potencial de acción) a lo largo del axón de una neurona, a todas las demás neuronas que están conectadas a ella. Esto permite que las señales se propaguen a lo largo de la estructura del cerebro humano.

Entonces, una neurona actúa como un interruptor de todo o nada, que toma un conjunto de entradas y genera un potencial de acción o ninguna salida.

– Página 66, Deep Learning, 2019.

Una red neuronal artificial es análoga a la estructura del cerebro humano, porque (1) está compuesta de manera similar por una gran cantidad de neuronas interconectadas que, (2) buscan propagar información a través de la red, (3) recibiendo conjuntos de estímulos desde las neuronas vecinas y mapeando estas a las salidas, para ser alimentadas a la siguiente capa de neuronas.

La estructura de una red neuronal artificial se organiza típicamente en capas de neuronas (recuerde la representación de un diagrama de árbol). Por ejemplo, el siguiente diagrama ilustra un red neuronal, donde todas las neuronas de una capa están conectadas a todas las neuronas de la siguiente capa:

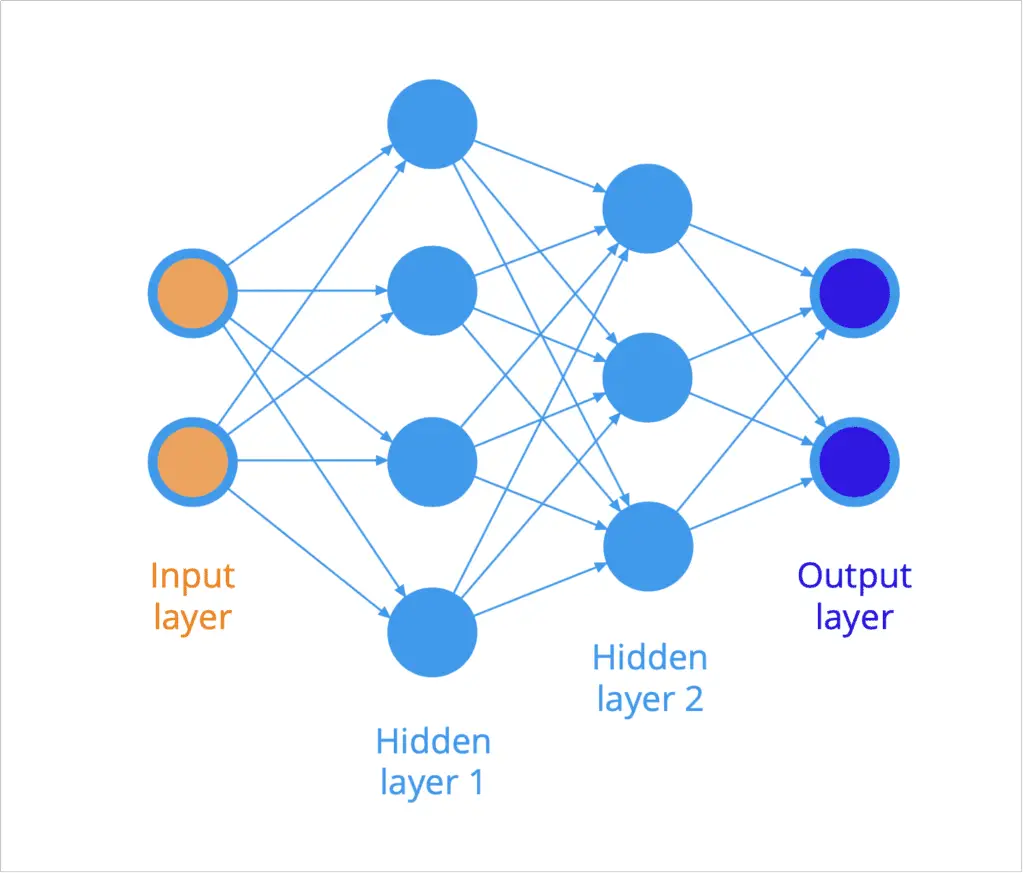
Una red neuronal feedforward completamente conectada

Las entradas se presentan en el lado izquierdo de la red y la información se propaga (o fluye) hacia la derecha hacia las salidas en el extremo opuesto. Dado que la información, por la presente, se propaga en el hacia adelante dirección a través de la red, entonces también nos referiremos a dicha red como un red neuronal feedforward.

Las capas de neuronas entre las capas de entrada y salida se denominan oculto capas, porque no son directamente accesibles.

A cada conexión (representada por una flecha en el diagrama) entre dos neuronas se le atribuye un peso, que actúa sobre los datos que fluyen por la red, como veremos en breve.

Las matemáticas de una neurona

Más específicamente, digamos que una neurona artificial particular (o una perceptrón, como Frank Rosenblatt lo había llamado inicialmente) recibe norte entradas, [x₁, …, x_n], donde a cada conexión se le atribuye un peso correspondiente, [w₁, …, w_n].

La primera operación que se realiza multiplica los valores de entrada por su peso correspondiente, y agrega un término de sesgo, B, a su suma, produciendo una salida, z:

z = ((X₁ × w₁) + (X₂ × w₂) +… + (X_norte × w_norte)) + B

Alternativamente, podemos representar esta operación en una forma más compacta de la siguiente manera:

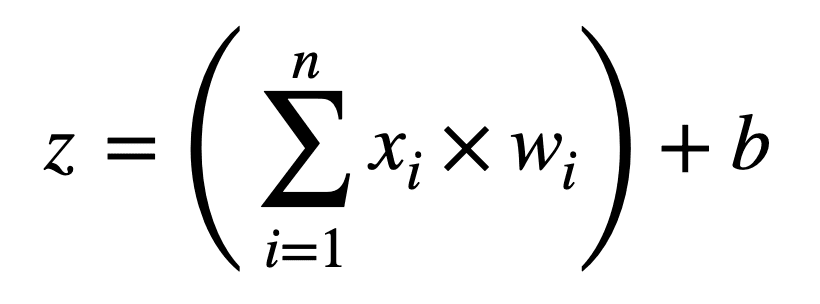
Este cálculo de suma ponderada que hemos realizado hasta ahora es una operación lineal. Si cada neurona tuviera que implementar este cálculo en particular por sí sola, entonces la red neuronal se limitaría a aprender solo asignaciones lineales de entrada y salida.

Sin embargo, muchas de las relaciones en el mundo que podríamos querer modelar no son lineales, y si intentamos modelar estas relaciones usando un modelo lineal, entonces el modelo será muy inexacto.

– Página 77, Deep Learning, 2019.

Por lo tanto, cada neurona realiza una segunda operación que transforma la suma ponderada mediante la aplicación de una función de activación no lineal, a(.):

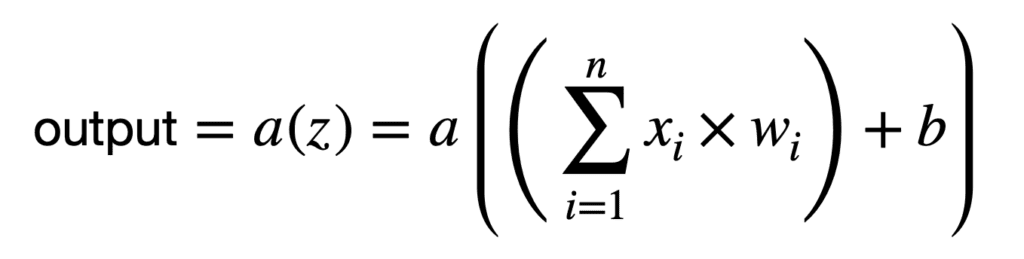
Podemos representar las operaciones realizadas por cada neurona de manera aún más compacta, si tuviéramos que integrar el término de sesgo en la suma como otro peso, w₀ (observe que la suma ahora comienza desde 0):

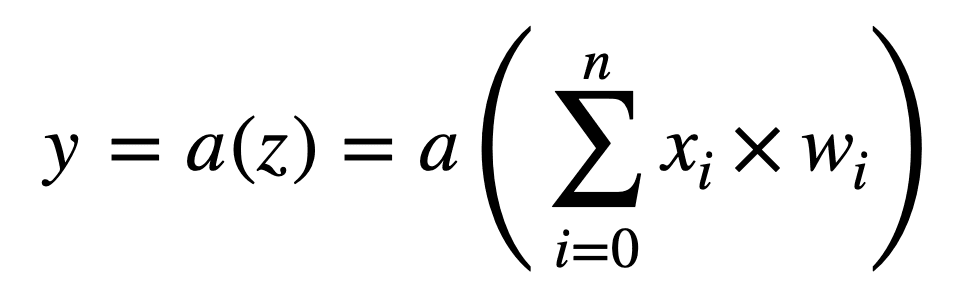
Las operaciones realizadas por cada neurona se pueden ilustrar de la siguiente manera:

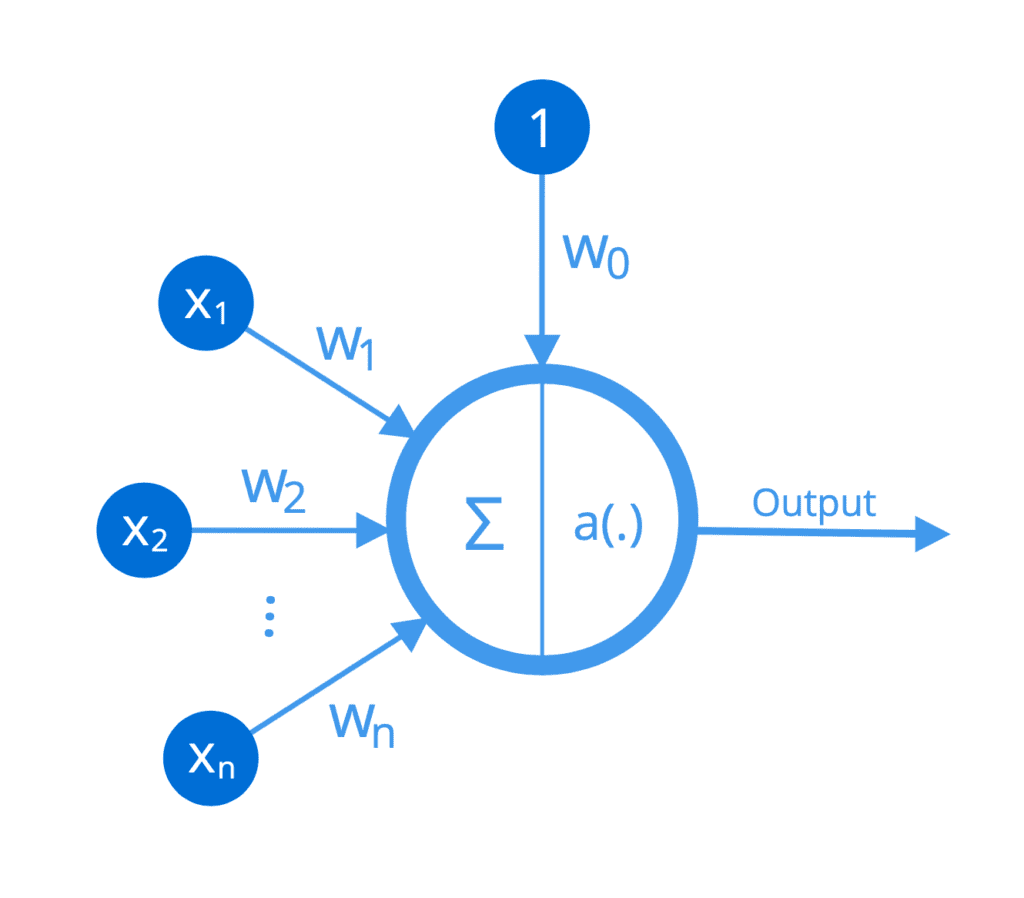
Función no lineal implementada por una neurona

Por lo tanto, se puede considerar que cada neurona implementa una función no lineal que asigna un conjunto de entradas a una activación de salida.

Entrenando a la Red

El entrenamiento de una red neuronal artificial implica el proceso de buscar el conjunto de pesos que mejor modele los patrones en los datos. Es un proceso que emplea los algoritmos de retropropagación y descenso de gradiente en tándem. Ambos algoritmos hacen un uso extensivo del cálculo.

Cada vez que la red se atraviesa en la dirección de avance (o hacia la derecha), el error de la red se puede calcular como la diferencia entre la salida producida por la red y la verdad esperada del terreno, por medio de una función de pérdida (como la suma de errores cuadrados (SSE)). El algoritmo de retropropagación, entonces, calcula el gradiente (o la tasa de cambio) de este error a los cambios en los pesos. Para hacerlo, requiere el uso de la regla de la cadena y derivadas parciales.

Para simplificar, considere una red formada por dos neuronas conectadas por una única ruta de activación. Si tuviéramos que abrirlos, encontraríamos que las neuronas realizan las siguientes operaciones en cascada:

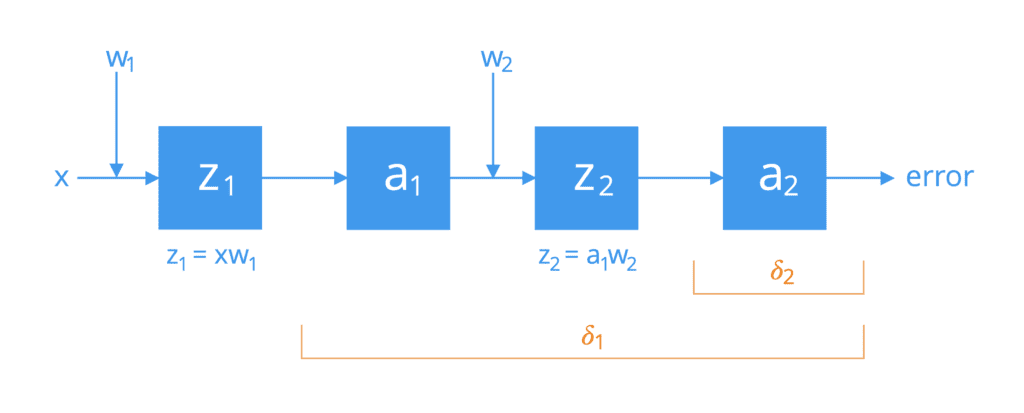
Operaciones realizadas por dos neuronas en cascada

La primera aplicación de la regla de la cadena conecta el error general de la red con la entrada, z₂, de la función de activación a₂ de la segunda neurona, y posteriormente al peso, w₂, como sigue:

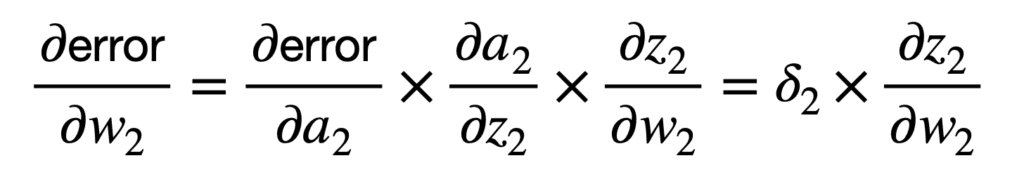
Puede notar que la aplicación de la regla de la cadena implica, entre otros términos, una multiplicación por la derivada parcial de la función de activación de la neurona con respecto a su entrada, z₂. Hay diferentes funciones de activación para elegir, como las funciones sigmoidea o logística. Si tuviéramos que tomar la función logística como ejemplo, entonces su derivada parcial se calcularía de la siguiente manera:

Por tanto, podemos calcular 𝛿₂ como sigue:

Aquí, t₂ es la activación esperada, y en encontrar la diferencia entre t₂ y a₂ estamos, por tanto, calculando el error entre la activación generada por la red y la verdad terrestre esperada.

Dado que estamos calculando la derivada de la función de activación, debería, por tanto, ser continua y diferenciable en todo el espacio de los números reales. En el caso de las redes neuronales profundas, el gradiente de error se propaga hacia atrás sobre una gran cantidad de capas ocultas. Esto puede hacer que la señal de error disminuya rápidamente a cero, especialmente si el valor máximo de la función derivada ya es pequeño para empezar (por ejemplo, la inversa de la función logística tiene un valor máximo de 0.25). Esto se conoce como problema de gradiente de desaparición. La función ReLU se ha utilizado tan popularmente en el aprendizaje profundo para aliviar este problema, porque su derivada en la parte positiva de su dominio es igual a 1.

El siguiente peso al revés está más profundo en la red y, por lo tanto, la aplicación de la regla de la cadena se puede extender de manera similar para conectar el error general al peso, w₁, como sigue:

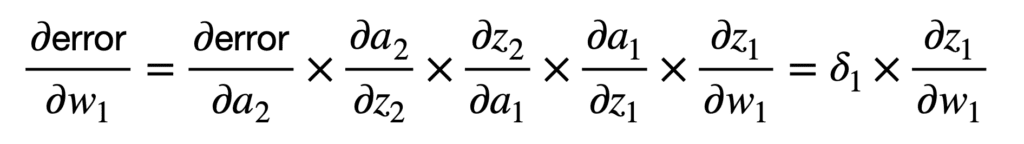
Si tomamos la función logística nuevamente como la función de activación de elección, entonces calcularíamos 𝛿₁ como sigue:

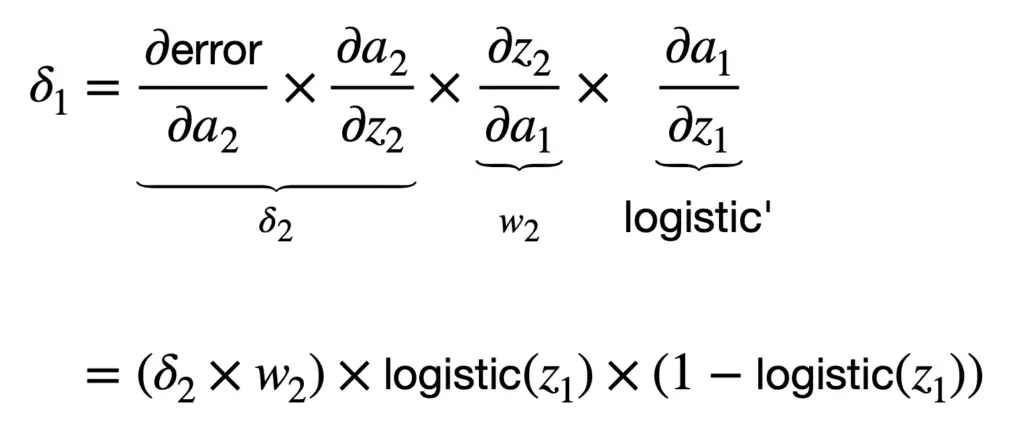
Una vez que hayamos calculado el gradiente del error de red con respecto a cada peso, entonces se puede aplicar el algoritmo de descenso de gradiente para actualizar cada peso para el siguiente. propagación hacia adelante en el momento, t+1. Por el peso w₁, la regla de actualización de peso que usa el descenso de gradiente se especificaría de la siguiente manera:

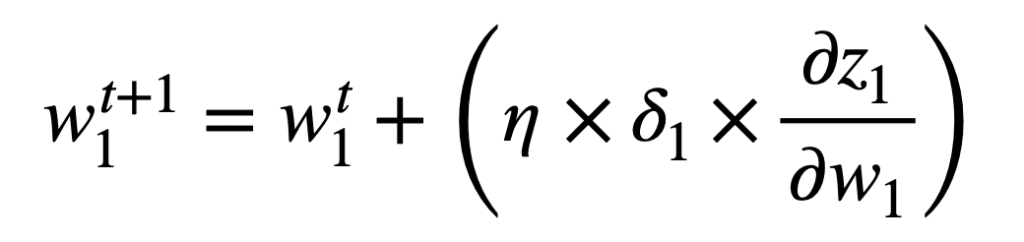
Aunque hemos considerado una red simple, el proceso por el que hemos pasado puede extenderse para evaluar otras más complejas y profundas, como las redes neuronales convolucionales (CNN).

Si la red en consideración se caracteriza por múltiples ramas provenientes de múltiples entradas (y posiblemente fluyendo hacia múltiples salidas), entonces su evaluación implicaría la suma de diferentes cadenas derivadas para cada ruta, de manera similar a como hemos derivado previamente la regla de la cadena generalizada.

Otras lecturas

Esta sección proporciona más recursos sobre el tema si desea profundizar.

Libros

Resumen

En este tutorial, descubrió cómo se aplican los aspectos del cálculo en las redes neuronales.

Específicamente, aprendiste:

• Una red neuronal artificial se organiza en capas de neuronas y conexiones, donde a cada una de estas últimas se le atribuye un valor ponderado.
• Cada neurona implementa una función no lineal que asigna un conjunto de entradas a una activación de salida.
• Al entrenar una red neuronal, los algoritmos de retropropagación y descenso de gradiente utilizan ampliamente el cálculo.

¿Tiene usted alguna pregunta?
Haga sus preguntas en los comentarios a continuación y haré todo lo posible para responder.