Análisis de sensibilidad del tamaño del conjunto de datos frente al rendimiento del modelo

El rendimiento del modelo de aprendizaje automático a menudo mejora con el tamaño del conjunto de datos para el modelado predictivo.

Esto depende de los conjuntos de datos específicos y de la elección del modelo, aunque a menudo significa que el uso de más datos puede generar un mejor rendimiento y que los descubrimientos realizados con conjuntos de datos más pequeños para estimar el rendimiento del modelo a menudo se escalan para utilizar conjuntos de datos más grandes.

El problema es que se desconoce la relación para un conjunto de datos y un modelo determinados, y es posible que no exista para algunos conjuntos de datos y modelos. Además, si tal relación existe, puede haber un punto o puntos de rendimientos decrecientes donde agregar más datos puede no mejorar el rendimiento del modelo o donde los conjuntos de datos son demasiado pequeños para capturar efectivamente la capacidad de un modelo a mayor escala.

Estos problemas se pueden solucionar realizando una análisis de sensibilidad para cuantificar la relación entre el tamaño del conjunto de datos y el rendimiento del modelo. Una vez calculados, podemos interpretar los resultados del análisis y tomar decisiones sobre cuántos datos son suficientes y qué tan pequeño puede ser un conjunto de datos para estimar eficazmente el rendimiento en conjuntos de datos más grandes.

En este tutorial, descubrirá cómo realizar un análisis de sensibilidad del tamaño del conjunto de datos frente al rendimiento del modelo.

Después de completar este tutorial, sabrá:

Seleccionar un tamaño de conjunto de datos para el aprendizaje automático es un problema abierto desafiante.
El análisis de sensibilidad proporciona un enfoque para cuantificar la relación entre el rendimiento del modelo y el tamaño del conjunto de datos para un modelo dado y un problema de predicción.
Cómo realizar un análisis de sensibilidad del tamaño del conjunto de datos e interpretar los resultados.

Empecemos.

Análisis de sensibilidad del tamaño del conjunto de datos frente al rendimiento del modelo
Foto de Graeme Churchard, algunos derechos reservados.

Descripción general del tutorial

Este tutorial se divide en tres partes; son:

Análisis de sensibilidad del tamaño del conjunto de datos
Tarea de predicción sintética y modelo de línea base
Análisis de sensibilidad del tamaño del conjunto de datos

Análisis de sensibilidad del tamaño del conjunto de datos

La cantidad de datos de entrenamiento necesarios para un modelo predictivo de aprendizaje automático es una cuestión abierta.

Depende de su elección de modelo, de la forma en que prepara los datos y de las características específicas de los datos en sí.

Para obtener más información sobre el desafío de seleccionar un tamaño de conjunto de datos de entrenamiento, consulte el tutorial:

Una forma de abordar este problema es realizar un análisis de sensibilidad y descubrir cómo varía el rendimiento de su modelo en su conjunto de datos con más o menos datos.

Esto podría implicar evaluar el mismo modelo con conjuntos de datos de diferentes tamaños y buscar una relación entre el tamaño del conjunto de datos y el rendimiento o un punto de rendimiento decreciente.

Normalmente, existe una fuerte relación entre el tamaño del conjunto de datos de entrenamiento y el rendimiento del modelo, especialmente para los modelos no lineales. La relación a menudo implica una mejora en el rendimiento hasta cierto punto y una reducción general en la varianza esperada del modelo a medida que aumenta el tamaño del conjunto de datos.

Conocer esta relación para su modelo y conjunto de datos puede ser útil por varias razones, como:

Evalúe más modelos.
Encuentra un modelo mejor.

Decide recopilar más datos.

Puede evaluar una gran cantidad de modelos y configuraciones de modelos rápidamente en una muestra más pequeña del conjunto de datos con la confianza de que el rendimiento probablemente se generalizará de una manera específica a un conjunto de datos de entrenamiento más grande.

Esto puede permitir evaluar muchos más modelos y configuraciones de los que podría realizar de otra manera dado el tiempo disponible y, a su vez, quizás descubrir un modelo de mejor rendimiento general.

También puede generalizar y estimar el rendimiento esperado del rendimiento del modelo a conjuntos de datos mucho más grandes y estimar si vale la pena el esfuerzo o el gasto de recopilar más datos de entrenamiento.

Ahora que estamos familiarizados con la idea de realizar un análisis de sensibilidad del rendimiento del modelo al tamaño del conjunto de datos, veamos un ejemplo trabajado.

Tarea de predicción sintética y modelo de línea base

Antes de sumergirnos en un análisis de sensibilidad, seleccionemos un conjunto de datos y un modelo de referencia para la investigación.

Usaremos un conjunto de datos de clasificación sintético binario (dos clases) en este tutorial. Esto es ideal ya que nos permite escalar el número de muestras generadas para el mismo problema según sea necesario.

La función make_classification () scikit-learn se puede utilizar para crear un conjunto de datos de clasificación sintético. En este caso, usaremos 20 características de entrada (columnas) y generaremos 1,000 muestras (filas). La semilla del generador de números pseudoaleatorios se fija para garantizar que se utilice el mismo «problema» base cada vez que se generen muestras.

El siguiente ejemplo genera el conjunto de datos de clasificación sintético y resume la forma de los datos generados.

# conjunto de datos de clasificación de prueba de sklearn.datasets importar make_classification # definir conjunto de datos X, y = make_classification (n_samples = 1000, n_features = 20, n_informative = 15, n_redundant = 5, random_state = 1) # resumir el conjunto de datos imprimir (forma X, forma y)<div id="ezoic-pub-ad-placeholder-720" data-inserter-version="2"></div>

# conjunto de datos de clasificación de prueba

desde sklearn.conjuntos de datos importar hacer_clasificación

# definir conjunto de datos

X, y = make_classification(n_samples=1000, n_features=20, n_informativo=15, n_redundante=5, estado_aleatorio=1)

# resumir el conjunto de datos

imprimir(X.forma, y.forma)

La ejecución del ejemplo genera los datos y reporta el tamaño de los componentes de entrada y salida, confirmando la forma esperada.

A continuación, podemos evaluar un modelo predictivo en este conjunto de datos.

Usaremos un árbol de decisiones (DecisionTreeClassifier) como modelo predictivo. Se eligió porque es un algoritmo no lineal y tiene una alta varianza, lo que significa que esperaríamos que el rendimiento mejorara con aumentos en el tamaño del conjunto de datos de entrenamiento.

Usaremos una mejor práctica de validación cruzada estratificada repetida de k veces para evaluar el modelo en el conjunto de datos, con 3 repeticiones y 10 pliegues.

El ejemplo completo de evaluación del modelo de árbol de decisión en el conjunto de datos de clasificación sintética se enumera a continuación.

# evaluar un modelo de árbol de decisión en el conjunto de datos de clasificación sintético de sklearn.datasets importar make_classification de sklearn.model_selection importar cross_val_score de sklearn.model_selection import RepeatedStratifiedKFold de sklearn.tree importar DecisionTreeClassifier # cargar conjunto de datos X, y = make_classification (n_samples = 1000, n_features = 20, n_informative = 15, n_redundant = 5, random_state = 1) # definir el procedimiento de evaluación del modelo cv = RepeatedStratifiedKFold (n_splits = 10, n_repeats = 3, random_state = 1) # definir modelo modelo = DecisionTreeClassifier () # evaluar modelo puntuaciones = cross_val_score (modelo, X, y, puntuación = ‘precisión’, cv = cv, n_jobs = -1) # informe de rendimiento print (‘Precisión media:% .3f (% .3f)’% (puntuaciones.mean (), puntuaciones.std ()))

# evaluar un modelo de árbol de decisión en el conjunto de datos de clasificación sintético

desde sklearn.conjuntos de datos importar make_classification

desde sklearn.model_selection importar cross_val_score

desde sklearn.model_selection importar Repetido estratificado KFold

desde sklearn.árbol importar DecisionTreeClassifier

# cargar conjunto de datos

X, y = make_classification(n_samples=1000, n_features=20, n_informativo=15, n_redundante=5, estado_aleatorio=1)

# definir el procedimiento de evaluación del modelo

CV = Repetido estratificado KFold(n_splits=10, n_repeats=3, estado_aleatorio=1)

# definir modelo

modelo = DecisionTreeClassifier()

# evaluar modelo

puntuaciones = cross_val_score(modelo, X, y, puntuación=‘precisión’, CV=CV, n_jobs=–1)

# informe de rendimiento

imprimir(‘Precisión media:% .3f (% .3f)’ % (puntuaciones.significar(), puntuaciones.std()))

La ejecución del ejemplo crea el conjunto de datos y luego estima el rendimiento del modelo en el problema utilizando el arnés de prueba elegido.

Nota: Sus resultados pueden variar dada la naturaleza estocástica del algoritmo o procedimiento de evaluación, o las diferencias en la precisión numérica. Considere ejecutar el ejemplo varias veces y compare el resultado promedio.

En este caso, podemos ver que la precisión de clasificación media es de aproximadamente 82,7%.

Precisión media: 0,827 (0,042)<div id="ezoic-pub-ad-placeholder-726" data-inserter-version="2"></div>

Precisión media: 0,827 (0,042)

A continuación, veamos cómo podríamos realizar un análisis de sensibilidad del tamaño del conjunto de datos sobre el rendimiento del modelo.

Análisis de sensibilidad del tamaño del conjunto de datos

La sección anterior mostró cómo evaluar un modelo elegido en el conjunto de datos disponible.

Plantea interrogantes como:

¿El modelo funcionará mejor con más datos?

De manera más general, podemos tener preguntas sofisticadas como:

¿El rendimiento estimado se mantiene en muestras más pequeñas o más grandes del dominio del problema?

Estas son preguntas difíciles de responder, pero podemos abordarlas mediante un análisis de sensibilidad. Específicamente, podemos usar un análisis de sensibilidad para aprender:

¿Qué tan sensible es el rendimiento del modelo al tamaño del conjunto de datos?

O más generalmente:

¿Cuál es la relación entre el tamaño del conjunto de datos y el rendimiento del modelo?

Hay muchas formas de realizar un análisis de sensibilidad, pero quizás el enfoque más simple es definir un arnés de prueba para evaluar el rendimiento del modelo y luego evaluar el mismo modelo en el mismo problema con conjuntos de datos de diferentes tamaños.

Esto permitirá que las porciones de entrenamiento y prueba del conjunto de datos aumenten con el tamaño del conjunto de datos general.

Para que el código sea más fácil de leer, lo dividiremos en funciones.

Primero, podemos definir una función que preparará (o cargará) el conjunto de datos de un tamaño dado. El número de filas en el conjunto de datos se especifica mediante un argumento a la función.

Si está utilizando este código como plantilla, esta función se puede cambiar para cargar su conjunto de datos desde un archivo y seleccionar una muestra aleatoria de un tamaño determinado.

# cargar conjunto de datos def load_dataset (n_samples): # definir el conjunto de datos X, y = make_classification (n_samples = int (n_samples), n_features = 20, n_informative = 15, n_redundant = 5, random_state = 1) devuelve X, y<div id="ezoic-pub-ad-placeholder-731" data-inserter-version="2"></div>

# cargar conjunto de datos

def load_dataset(n_samples):

# definir el conjunto de datos

X, y = make_classification(n_samples=En t(n_samples), n_features=20, n_informativo=15, n_redundante=5, estado_aleatorio=1)

regreso X, y

A continuación, necesitamos una función para evaluar un modelo en un conjunto de datos cargado.

Definiremos una función que toma un conjunto de datos y devuelve un resumen del rendimiento del modelo evaluado utilizando el arnés de prueba en el conjunto de datos.

Esta función se enumera a continuación, toma los elementos de entrada y salida de un conjunto de datos y devuelve la desviación media y estándar del modelo de árbol de decisión en el conjunto de datos.

<div id="ezoic-pub-ad-placeholder-733" data-inserter-version="2"></div> # evaluar un modelo def modelo_evaluación (X, y): # definir el procedimiento de evaluación del modelo cv = RepeatedStratifiedKFold (n_splits = 10, n_repeats = 3, random_state = 1) # definir modelo modelo = DecisionTreeClassifier () # evaluar modelo puntuaciones = cross_val_score (modelo, X, y, puntuación = ‘precisión’, cv = cv, n_jobs = -1) # devuelve estadísticas de resumen regreso [scores.mean(), scores.std()]

# evaluar un modelo

def evaluar_modelo(X, y):

# definir el procedimiento de evaluación del modelo

CV = Repetido estratificado KFold(n_splits=10, n_repeats=3, estado_aleatorio=1)

# definir modelo

modelo = DecisionTreeClassifier()

# evaluar modelo

puntuaciones = cross_val_score(modelo, X, y, puntuación=‘precisión’, CV=CV, n_jobs=–1)

# devuelve estadísticas de resumen

regreso [[puntuaciones.significar(), puntuaciones.std()]

A continuación, podemos definir un rango de diferentes tamaños de conjuntos de datos para evaluar.

Los tamaños deben elegirse proporcionalmente a la cantidad de datos que tiene disponible y la cantidad de tiempo de ejecución que está dispuesto a invertir.

En este caso, mantendremos los tamaños modestos para limitar el tiempo de ejecución, de 50 a un millón de filas en una escala de log10 aproximada.

… # definir el número de muestras a considerar tamaños = [50, 100, 500, 1000, 5000, 10000, 50000, 100000, 500000, 1000000]

...

# definir el número de muestras a considerar

tamaños = [[50, 100, 500, 1000, 5000, 10000, 50000, 100000, 500000, 1000000]

A continuación, podemos enumerar el tamaño de cada conjunto de datos, crear el conjunto de datos, evaluar un modelo en el conjunto de datos y almacenar los resultados para un análisis posterior.

<div id="ezoic-pub-ad-placeholder-737" data-inserter-version="2"></div> … # evaluar cada número de muestras significa, stds = list (), list () para n_samples en tamaños: # obtener un conjunto de datos X, y = load_dataset (n_samples) # evaluar un modelo en este tamaño de conjunto de datos mean, std = evalu_modelo (X, y) # Tienda means.append (media) stds.append (std)

...

# evaluar cada número de muestras

medio, ETS = lista(), lista()

por n_samples en tamaños:

# obtener un conjunto de datos

X, y = load_dataset(n_samples)

# evaluar un modelo en este tamaño de conjunto de datos

significar, std = evaluar_modelo(X, y)

# Tienda

medio.adjuntar(significar)

ETS.adjuntar(std)

A continuación, podemos resumir la relación entre el tamaño del conjunto de datos y el rendimiento del modelo.

En este caso, simplemente trazaremos el resultado con barras de error para que podamos detectar cualquier tendencia visualmente.

Usaremos la desviación estándar como una medida de incertidumbre sobre el desempeño estimado del modelo. Esto se puede lograr multiplicando el valor por 2 para cubrir aproximadamente el 95% del rendimiento esperado si el rendimiento sigue una distribución normal.

Esto se puede mostrar en el gráfico como una barra de error alrededor del rendimiento medio esperado para un tamaño de conjunto de datos.

… # defina la barra de error como 2 desviaciones estándar de la media o 95% err = [min(1, s * 2) for s in stds] # trazar el tamaño del conjunto de datos frente al rendimiento medio con barras de error pyplot.errorbar (tamaños, medias, yerr = err, fmt = «- o»)<div id="ezoic-pub-ad-placeholder-740" data-inserter-version="2"></div>

...

# defina la barra de error como 2 desviaciones estándar de la media o 95%

errar = [[min(1, s * 2) por s en ETS]

# trazar el tamaño del conjunto de datos frente al rendimiento medio con barras de error

pyplot.Barra de error(tamaños, medio, yerr=errar, fmt=‘-o’)

Para que el gráfico sea más legible, podemos cambiar la escala del eje x a log, dado que los tamaños de nuestro conjunto de datos están en una escala aproximada log10.

… # cambiar la escala del eje x para registrar ax = pyplot.gca () ax.set_xscale («registro», no positivo = «clip») # mostrar la trama pyplot.show ()

...

# cambiar la escala del eje x para registrar

hacha = pyplot.gca()

hacha.set_xscale(«Iniciar sesión», no positivo=‘acortar’)

# mostrar la trama

pyplot.show()

Y eso es.

En general, esperaríamos que el rendimiento medio del modelo aumentara con el tamaño del conjunto de datos. También esperaríamos que la incertidumbre en el desempeño del modelo disminuya con el tamaño del conjunto de datos.

Al unir todo esto, a continuación se enumera el ejemplo completo de cómo realizar un análisis de sensibilidad del tamaño del conjunto de datos sobre el rendimiento del modelo.

# análisis de sensibilidad del rendimiento del modelo al tamaño del conjunto de datos de sklearn.datasets importar make_classification de sklearn.model_selection importar cross_val_score de sklearn.model_selection import RepeatedStratifiedKFold de sklearn.tree importar DecisionTreeClassifier desde matplotlib importar pyplot<div id="ezoic-pub-ad-placeholder-744" data-inserter-version="2"></div> # cargar conjunto de datos def load_dataset (n_samples): # definir el conjunto de datos X, y = make_classification (n_samples = int (n_samples), n_features = 20, n_informative = 15, n_redundant = 5, random_state = 1) devuelve X, y # evaluar un modelo def modelo_evaluación (X, y): # definir el procedimiento de evaluación del modelo cv = RepeatedStratifiedKFold (n_splits = 10, n_repeats = 3, random_state = 1) # definir modelo modelo = DecisionTreeClassifier () # evaluar modelo puntuaciones = cross_val_score (modelo, X, y, puntuación = ‘precisión’, cv = cv, n_jobs = -1) # devuelve estadísticas de resumen regreso [scores.mean(), scores.std()] # definir el número de muestras a considerar tamaños = [50, 100, 500, 1000, 5000, 10000, 50000, 100000, 500000, 1000000] # evaluar cada número de muestras significa, stds = list (), list () para n_samples en tamaños: # obtener un conjunto de datos X, y = load_dataset (n_samples) # evaluar un modelo en este tamaño de conjunto de datos mean, std = evalu_modelo (X, y) # Tienda means.append (media) stds.append (std) # resumir el rendimiento print (‘>% d:% .3f (% .3f)’% (n_samples, mean, std)) # defina la barra de error como 2 desviaciones estándar de la media o 95% err = [min(1, s * 2) for s in stds] # trazar el tamaño del conjunto de datos frente al rendimiento medio con barras de error pyplot.errorbar (tamaños, medias, yerr = err, fmt = «- o») # cambiar la escala del eje x para registrar ax = pyplot.gca () ax.set_xscale («registro», no positivo = «clip») # mostrar la trama pyplot.show ()<div id="ezoic-pub-ad-placeholder-745" data-inserter-version="2"></div>

dieciséis

# análisis de sensibilidad del rendimiento del modelo al tamaño del conjunto de datos

desde sklearn.conjuntos de datos importar make_classification

desde sklearn.model_selection importar cross_val_score

desde sklearn.model_selection importar Repetido estratificado KFold

desde sklearn.árbol importar DecisionTreeClassifier

desde matplotlib importar pyplot

# cargar conjunto de datos

def load_dataset(n_samples):

# definir el conjunto de datos

X, y = make_classification(n_samples=En t(n_samples), n_features=20, n_informativo=15, n_redundante=5, estado_aleatorio=1)

regreso X, y

# evaluar un modelo

def evaluar_modelo(X, y):

# definir el procedimiento de evaluación del modelo

CV = Repetido estratificado KFold(n_splits=10, n_repeats=3, estado_aleatorio=1)

# definir modelo

modelo = DecisionTreeClassifier()

# evaluar modelo

puntuaciones = cross_val_score(modelo, X, y, puntuación=‘precisión’, CV=CV, n_jobs=–1)

# devuelve estadísticas de resumen

regreso [[puntuaciones.significar(), puntuaciones.std()]

# definir el número de muestras a considerar

tamaños = [[50, 100, 500, 1000, 5000, 10000, 50000, 100000, 500000, 1000000]

# evaluar cada número de muestras

medio, ETS = lista(), lista()

por n_samples en tamaños:

# obtener un conjunto de datos

X, y = load_dataset(n_samples)

# evaluar un modelo en este tamaño de conjunto de datos

significar, std = evaluar_modelo(X, y)

# Tienda

medio.adjuntar(significar)

ETS.adjuntar(std)

# resumir el rendimiento

imprimir(‘>% d:% .3f (% .3f)’ % (n_samples, significar, std))

# defina la barra de error como 2 desviaciones estándar de la media o 95%

errar = [[min(1, s * 2) por s en ETS]

# trazar el tamaño del conjunto de datos frente al rendimiento medio con barras de error

pyplot.Barra de error(tamaños, medio, yerr=errar, fmt=‘-o’)

# cambiar la escala del eje x para registrar

hacha = pyplot.gca()

hacha.set_xscale(«Iniciar sesión», no positivo=‘acortar’)

# mostrar la trama

pyplot.show()

La ejecución del ejemplo informa el estado a lo largo del camino del tamaño del conjunto de datos frente al rendimiento estimado del modelo.

En este caso, podemos ver la tendencia esperada de aumentar el rendimiento medio del modelo con el tamaño del conjunto de datos y disminuir la varianza del modelo medida utilizando la desviación estándar de la precisión de la clasificación.

Podemos ver que quizás haya un punto de rendimientos decrecientes al estimar el rendimiento del modelo en quizás 10,000 o 50,000 filas.

Específicamente, vemos una mejora en el rendimiento con más filas, pero probablemente podamos capturar esta relación con poca variación con 10K o 50K filas de datos.

También podemos ver una caída en el rendimiento estimado con 1,000,000 de filas de datos, lo que sugiere que probablemente estamos maximizando la capacidad del modelo por encima de 100,000 filas y, en cambio, estamos midiendo el ruido estadístico en la estimación.

Esto podría significar un límite superior en el rendimiento esperado y probablemente más datos más allá de este punto no mejorarán el modelo y la configuración específicos en el arnés de prueba elegido.

> 50: 0,673 (0,141) > 100: 0,703 (0,135) > 500: 0,809 (0,055) > 1000: 0,826 (0,044) > 5000: 0,835 (0,016) > 10000: 0,866 (0,011) > 50000: 0,900 (0,005) > 100000: 0,912 (0,003) > 500000: 0,938 (0,001) > 1000000: 0,936 (0,001)

> 50: 0,673 (0,141)

> 100: 0,703 (0,135)

> 500: 0,809 (0,055)

> 1000: 0,826 (0,044)

> 5000: 0,835 (0,016)

> 10000: 0,866 (0,011)

> 50000: 0,900 (0,005)

> 100000: 0,912 (0,003)

> 500000: 0,938 (0,001)

> 1000000: 0,936 (0,001)

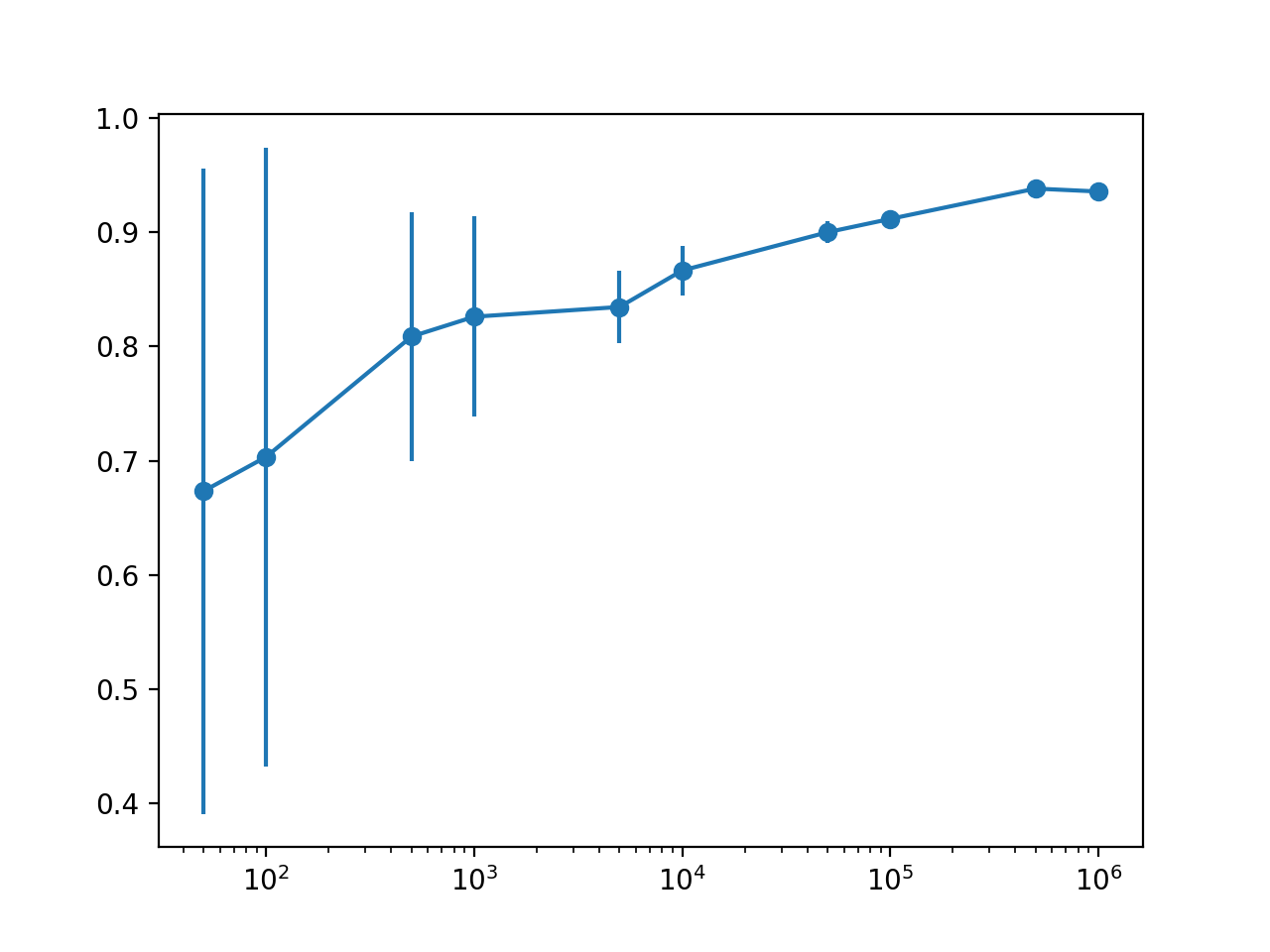
El gráfico hace que la relación entre el tamaño del conjunto de datos y el rendimiento estimado del modelo sea mucho más clara.

La relación es casi lineal con un tamaño de conjunto de datos de registro. El cambio en la incertidumbre que se muestra como la barra de error también disminuye drásticamente en el gráfico de valores muy grandes con 50 o 100 muestras, a valores modestos con 5,000 y 10,000 muestras y prácticamente superó estos tamaños.

Dada la modesta distribución con 5.000 y 10.000 muestras y la relación prácticamente log-lineal, probablemente podríamos salirse con la suya utilizando filas de 5K o 10K para aproximar el rendimiento del modelo.

Gráfico de línea con barras de error del tamaño del conjunto de datos frente al rendimiento del modelo

Podríamos usar estos hallazgos como base para probar configuraciones de modelos adicionales e incluso diferentes tipos de modelos.

El peligro es que los diferentes modelos pueden funcionar de manera muy diferente con más o menos datos y puede ser conveniente repetir el análisis de sensibilidad con un modelo diferente elegido para confirmar que la relación se mantiene. Alternativamente, puede ser interesante repetir el análisis con un conjunto de diferentes tipos de modelos.

Otras lecturas

Esta sección proporciona más recursos sobre el tema si está buscando profundizar.

Tutoriales

API

Artículos

Resumen

En este tutorial, descubrió cómo realizar un análisis de sensibilidad del tamaño del conjunto de datos frente al rendimiento del modelo.

Específicamente, aprendiste:

Seleccionar un tamaño de conjunto de datos para el aprendizaje automático es un problema abierto desafiante.
El análisis de sensibilidad proporciona un enfoque para cuantificar la relación entre el rendimiento del modelo y el tamaño del conjunto de datos para un modelo dado y un problema de predicción.
Cómo realizar un análisis de sensibilidad del tamaño del conjunto de datos e interpretar los resultados.

¿Tiene usted alguna pregunta?
Haga sus preguntas en los comentarios a continuación y haré todo lo posible para responder.

¡Descubra el aprendizaje automático rápido en Python!

Desarrolle sus propios modelos en minutos

… con solo unas pocas líneas de código scikit-learn

Aprenda cómo en mi nuevo libro electrónico:
Dominio del aprendizaje automático con Python

Cubiertas tutoriales de autoaprendizaje y proyectos de principio a fin me gusta:
Cargando datos, visualización, modelado, Afinación, y mucho más…

Finalmente, lleve el aprendizaje automático a
Tus Propios Proyectos

Sáltate los académicos. Solo resultados.

Mira lo que hay dentro

Descripción general del tutorial

Análisis de sensibilidad del tamaño del conjunto de datos

Tarea de predicción sintética y modelo de línea base

Análisis de sensibilidad del tamaño del conjunto de datos

Otras lecturas

Tutoriales

API

Artículos

Resumen

¡Descubra el aprendizaje automático rápido en Python!

Desarrolle sus propios modelos en minutos

Finalmente, lleve el aprendizaje automático a Tus Propios Proyectos

Finalmente, lleve el aprendizaje automático a
Tus Propios Proyectos