Muchas de las tareas que hacemos regularmente, como navegar por una ciudad, cocinar un
comida, o la carga de un lavavajillas, requieren una planificación durante largos períodos de tiempo.
Cumplir estas tareas puede parecernos simple; sin embargo, razonar durante mucho tiempo
Los horizontes temporales siguen siendo un gran desafío para el Aprendizaje de Refuerzo (RL) de hoy en día
algoritmos. Aunque no pueden planear sobre horizontes largos, los algoritmos de RL profundos sobresalen
en las políticas de aprendizaje para tareas de corto plazo, como el agarre robótico,
directamente de los píxeles. Al mismo tiempo, los métodos clásicos de planificación como
El algoritmo de Dijkstra y la búsqueda de A$^*$ pueden planear sobre horizontes de tiempo largos, pero
requieren representaciones abstractas especificadas a mano o por tarea de la
ambiente como entrada.
Para lograr lo mejor de ambos mundos, los métodos de navegación visual de última generación
han aplicado los métodos clásicos de búsqueda a los gráficos aprendidos. En particular, el SPTM [2]
y SoRB [3] usar un buffer de repetición de observaciones como nodos en un gráfico y aprender
una función de distancia paramétrica para dibujar bordes en el gráfico. Estos métodos tienen
se han aplicado con éxito a tareas de navegación simulada de largo plazo que fueron
demasiado difícil de resolver para los métodos anteriores.
No obstante, estos métodos siguen siendo limitados porque son altamente sensibles
a los errores en el gráfico aprendido. Incluso un solo borde defectuoso actúa como un agujero de gusano
en la topología de los gráficos que los algoritmos de planificación tratan de explotar, lo que hace
métodos existentes que combinan la búsqueda de gráficos y RL extremadamente frágil. Para
Por ejemplo, si un agente artificial que navega por un laberinto piensa que dos observaciones
a ambos lados de un muro están cerca, sus planes implicarán transiciones que
chocar contra la pared. Adoptando un modelo simple que asume una constante
probabilidad $p$ de que cada borde sea defectuoso, vemos que el número esperado de
los bordes defectuosos es $p|E| = O(|V|^^2)$. En otras palabras, errores en la escala del gráfico
cuadráticamente con el número de nodos en el gráfico.
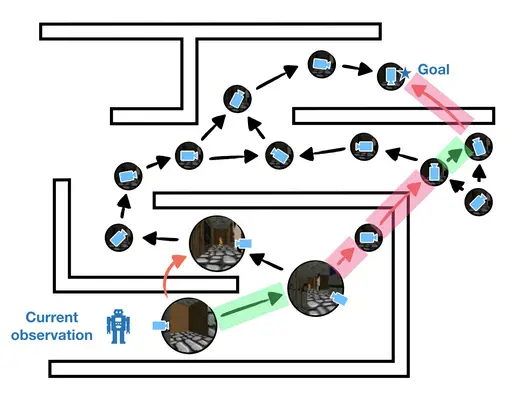
Podríamos hacerlo mucho mejor si pudiéramos minimizar los errores en el gráfico. ¿Pero cómo?
Los gráficos sobre las observaciones tanto en ambientes simulados como en el mundo real pueden ser
prohibitivo, lo que hace difícil incluso identificar qué bordes son
…defectuoso. Para minimizar los errores en el gráfico, entonces, deseamos la escasez; queremos
mantener un conjunto mínimo de nodos que sea suficiente para la planificación. Si tenemos una forma
para agregar observaciones similares en un solo nodo del gráfico, podemos
reducir el número de errores y mejorar la precisión de nuestros planes. La clave
El desafío es agregar las observaciones de manera que se respete la temporalidad.
…las restricciones. Si las observaciones son similares en apariencia pero en realidad están muy lejos,
entonces deben ser agregados en diferentes nodos.
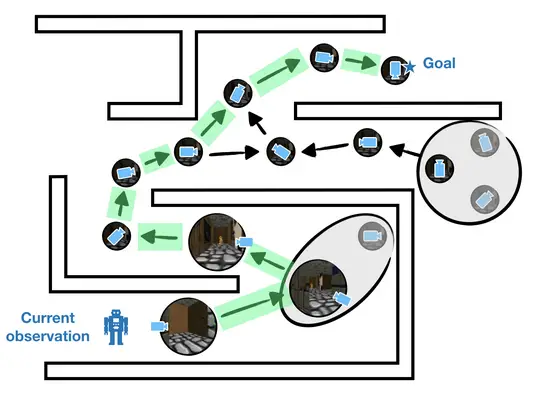
Entonces, ¿cómo podemos esparcir nuestro gráfico mientras garantizamos que el gráfico permanezca
útil para la planificación? Nuestra visión clave es un novedoso criterio de fusión llamado
consistencia de doble sentido. La consistencia bidireccional puede ser vista como una generalización de
valoran la irrelevancia para el ajuste del objetivo condicionado. Intuitivamente, la consistencia bidireccional
fusiona nodos (i) que pueden ser intercambiados como estados iniciales y (ii) que pueden ser
intercambiados como estados de meta.
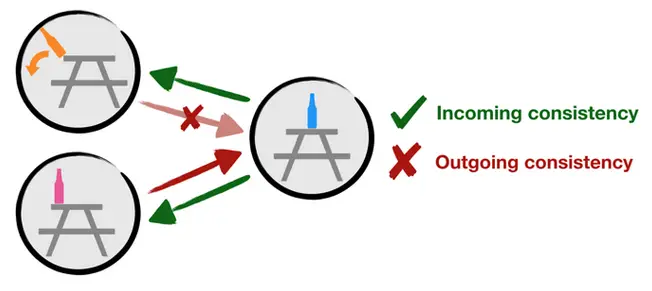
Para un ejemplo de consistencia bidireccional, considere la figura anterior. Supongamos que
durante nuestro procedimiento de fusión de nodos nos preguntamos: ¿podemos fusionar los nodos con rosa y
botellas de naranja de acuerdo con la consistencia de dos vías? Primero, notamos que el movimiento
de la botella azul a la botella rosa requiere aproximadamente el mismo trabajo que
pasando de la botella azul a la botella naranja. Así que los nodos con rosa y
las botellas naranjas satisfacen el criterio (ii) porque pueden ser intercambiadas como objetivo
…estados. Sin embargo, aunque es posible empezar desde la botella rosa y pasar a
la botella azul, si en vez de eso empezamos con la botella naranja, la botella naranja
…caerá al suelo y se estrellará! Así que los nodos con botellas rosas y naranjas
fallan en el criterio (i) porque no pueden ser intercambiados como estados de partida.
En la práctica, no podemos esperar encontrar dos nodos que pueden ser perfectamente
intercambiado. En su lugar, fusionamos nodos que pueden ser intercambiados hasta un
parámetro de umbral $tau$. Aumentando $tau$, podemos hacer que el resultado
gráfico tan disperso como nos gustaría. Crucialmente, *demostramos en el periódico que la fusión
de acuerdo a la consistencia de dos vías preserva la calidad del gráfico hasta un error
término que se escala sólo linealmente con el umbral de fusión $tau$.
Nuestra motivación para la escasez, discutida anteriormente, es la robustez: esperamos que los más pequeños
gráficos para tener menos errores. Además, nuestro teorema principal nos dice que podemos
fusionar los nodos de acuerdo a la consistencia de dos vías, mientras se preserva el gráfico
calidad. Experimentalmente, sin embargo, ¿son más robustos los escasos gráficos resultantes?
Para probar la robustez de la memoria gráfica dispersa a los errores en la distancia aprendida
métricas, adelgazamos las paredes en los laberintos de PointEnv de [3]. Mientras que PointEnv es un
ambiente simple con observaciones de coordenadas $(x, y)$, adelgazar las paredes es
un gran desafío para las funciones de distancia paramétrica; cualquier error en el aprendizaje
función de distancia causará bordes defectuosos a través de las paredes que destruyen la
la viabilidad de los planes. Por esta razón, simplemente adelgazar las paredes del laberinto es suficiente
para romper el anterior estado de la técnica [3] resultando en una tasa de éxito del 0%.
¿Qué tal va la memoria gráfica dispersa? Con muchos menos bordes, se convierte en
para realizar una limpieza auto-supervisada: el agente puede atravesar el
para detectar y eliminar los bordes defectuosos de su gráfico. La siguiente figura
ilustra los resultados de este proceso. Mientras que el gráfico denso que se muestra en rojo tiene
muchos bordes defectuosos, la escasez y la limpieza auto-supervisada, se muestra en verde,
superar los errores en la métrica de la distancia aprendida, lo que lleva a una tasa de éxito del 100%.
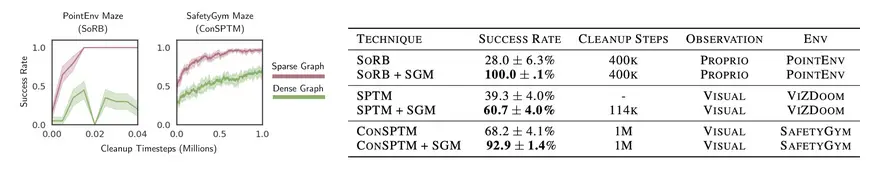
Vemos una tendencia similar en los experimentos con entrada visual. Tanto en ViZDoom [4]
y SafetyGym [5] – tareas de navegación en el laberinto que requieren una planificación desde el principio
imágenes – La escasa memoria gráfica mejora constantemente el éxito de la línea de base
métodos que incluyen SoRB [3] y SPTM [2].
Además de contener menos errores, la escasa memoria gráfica también da lugar a
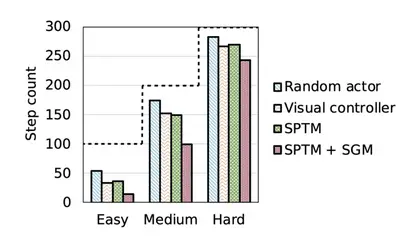
planes más óptimos. En una tarea de navegación en el laberinto de ViZDoom [4]encontramos que el SGM
requiere significativamente menos pasos para alcanzar el objetivo final a través de fácil, medio,
y tareas duras del laberinto, lo que significa que el agente sigue un camino más corto hacia el final
destino.
En general, encontramos que la agregación de estados con una consistencia bidireccional dio como resultado
planes sustancialmente más robustos que el estado de la técnica anterior. Mientras que
prometedoras, quedan muchas preguntas abiertas y desafíos para combinar la clásica
planificación con control basado en el aprendizaje. Algunas de las preguntas que estamos pensando
¿Cómo podemos extender estos métodos más allá de la navegación a la manipulación
dominios? Como el mundo no es estático, ¿cómo deberíamos construir gráficos sobre los cambios
ambientes? ¿Cómo puede utilizarse la coherencia bidireccional más allá del alcance de
métodos de planificación basados en gráficos? Estamos entusiasmados con estas direcciones futuras
y esperamos que nuestros hallazgos teóricos y experimentales sean útiles para otros
los investigadores que investigan el control sobre los horizontes temporales extendidos.
Referencias
- Emmons*, Jain*, Laskin* y otros. Memoria gráfica dispersa para una planificación robusta. NeurIPS 2020.
- Savinov y otros. Memoria topológica semiparamétrica para la navegación. ICLR 2019.
- Eysenbach et al. Busca en el buffer de reproducción: Uniendo el aprendizaje de la planificación y el refuerzo. NeurIPS 2020.
- Wydmuch y otros. Competiciones ViZDoom: Jugar a Doom desde Pixels. Transacciones IEEE sobre los Juegos, 2018.
- Ray et al. Benchmarking Safe Exploration in Deep Reinforcement Learning. Preprint, 2019.
